-
Определите количество натуральных чисел, не превосходящих 100, которые не делятся ни на 3, ни на 5.
100 / 3 = 33 – делится на 3
100 / 5 = 20 – делится на 5
100 / (3∙5) = 100 / 15 = 6 – делится и на 3, и на 5
100 – 33 – 20 – 6 = 53 – не делится ни на 3, ни на 5
11. Постройте для неориентированного графа матрицы смежности и инцидентности, сопряженный (реберный) граф.
1 a1 a2
2 5 a3
a4 a5
3 4 a6
Матрица смежности
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
2 |
1 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
0 |
1 |
0 |
|
4 |
1 |
0 |
1 |
0 |
1 |
|
5 |
1 |
0 |
0 |
1 |
0 |
Матрица инцидентности
|
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
2 |
0 |
1 |
0 |
0 |
1 |
0 |
|
3 |
0 |
0 |
0 |
0 |
1 |
1 |
|
4 |
0 |
0 |
1 |
1 |
0 |
1 |
|
5 |
1 |
0 |
0 |
1 |
0 |
0 |
Сопряженный (реберный) граф
1
5
2
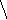
3 6
4
12. Изобразите неориентированный граф со множеством V = {a,b,c,d} вершин и множеством E={(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)} ребер. Составьте его матрицы смежности и инцидентности. Определите степени вершин. Выясните, является ли он планарным.
1
b a c d 2 4 6
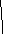
3
5
Матрица смежности
|
|
a |
b |
c |
d |
|
a |
0 |
1 |
1 |
1 |
|
b |
1 |
0 |
1 |
1 |
|
c |
1 |
1 |
0 |
1 |
|
d |
1 |
1 |
1 |
0 |
Матрица инцидентности
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
a |
1 |
1 |
1 |
0 |
0 |
0 |
|
b |
1 |
0 |
0 |
1 |
1 |
0 |
|
c |
0 |
1 |
0 |
1 |
0 |
1 |
|
d |
0 |
0 |
1 |
0 |
1 |
1 |
Степени вершин:
d(a) = 3
d(b) = 3
d(c) = 3
d(d) = 3
Данный граф является планарным, так как его можно изобразить на плоскости без пересечения ребер.
14. Изобразите орграф со множеством V={a,b,c,d} вершин и множеством E={(a,b),(b,c),(b,d),(c,d),(d,a),(d,b)} дуг. Составьте его матрицы смежности и инцидентности. Определите полустепени входа и выхода его вершин.
1
b a c d
2 3 5
4
6
Матрица смежности
|
|
a |
b |
c |
d |
|
a |
0 |
1 |
0 |
0 |
|
b |
0 |
0 |
1 |
1 |
|
c |
0 |
0 |
0 |
1 |
|
d |
1 |
1 |
0 |
0 |
Матрица инцидентности
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
a |
-1 |
1 |
0 |
0 |
0 |
0 |
|
b |
0 |
-1 |
1 |
-1 |
0 |
1 |
|
c |
0 |
0 |
0 |
0 |
1 |
-1 |
|
d |
1 |
0 |
-1 |
1 |
-1 |
0 |
Полустепени входа:
d+(a)=1
d+(b)=2
d+(c)=1
d+(d)=2
Полустепени выхода:
d-(a)=1
d-(b)=2
d-(c)=1
d-(d)=2
19. Постройте плоский граф, изоморфный полному, состоящему из 4 вершин.
Полный граф
b a c d
Изоморфный ему плоский граф
a c d
b
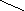
20. Определите, изоморфны ли графы.
Изоморфны, так как номера вершин можно подобрать так, чтобы матрицы смежности графов совпадали.
21. Постройте граф, для которого задана матрица смежности.
1
2 5
3 4
22. Постройте орграф по его матрице смежности
b a c d
