Методические рекомендации по выполнению КОНТРОЛЬНОЙ 1

дисциплина: "Экономико-математические методы в организации транспортного процесса"

Для решения первой задачи необходимо уметь выполнять следующие частные задания.

1. Построить математическую модель в форме задачи линейного программирования.

Методику выполнения первого и второго частных заданий будем иллюстрировать на примере 1.

Пример 1. Имеется возможность производить два вида продукции, при этом происходит потребление ресурсов четырех типов, запасы которых составляют соответственно 16, 12, 8 и 12 единиц. При производстве единицы продукции первого вида расходуется 4, 0, 1 и 2 единицы соответствующего ресурса, прибыль от реализации единицы этой продукции составляет 20 денежных единиц. При производстве единицы продукции второго вида расходуется соответственно 0, 4, 2 и 2 единицы ресурсов, прибыль - 30 денежных единиц. Определить сколько продукции каждого вида надо произвести с тем, чтобы суммарная прибыль от ее реализации была максимальной. Проблем со сбытом не возникает.

Критерием эффективности здесь является суммарная прибыль. Учитываемыми факторами, от которых эта прибыль зависит, являются: объемы запасов ресурсов, их расход при производстве единицы продукции, прибыль за единицу продукции. Эти факторы не управляемые. Прибыль зависит еще и от двух управляемых факторов - объемов производимой продукции первого и второго типа.

Обозначим: - объем производства продукции первого типа; - второго. Тогда суммарная прибыль от произведенной продукции равна: .

Организуя производство, необходимо учитывать, что запасы ресурсов ограничены, т.е. неизвестные задачи должны удовлетворять условиям:

Еще одна группа условий связана с тем, что неизвестные не могут быть отрицательными. С учетом всего сказанного получаем следующую математическую модель:

,

1.2. Найти оптимальный план производства, используя геометрическую интерпретацию задачи линейного программирования.

Задача из примера 1 содержит две переменные – x₁ и x₂. Изобразим ее условия на координатной плоскости Ox₁x₂. Прежде всего построим множество точек, соответствующих допустимым планам задачи, т.е. множество точек, координаты которых удовлетворяют всем шести условиям задачи.

Множеству допустимых планов задачи на рисунке соответствует заштрихованная область.

Рассмотрим теперь целевую функцию. Так как она является линейной функцией, то её линии уровня являются прямыми и при этом, все линии уровня параллельны. Напомним, что линией уровня функции называется множество всех таких точек из области определения функции, на которых она принимает одинаковые значения. Построим на графике одну из линий уровня целевой функции, например, соответствующую значению 60, т.е. построим прямую, задаваемую уравнением:

20x₁ + 30x₂ = 60.

Обозначим эту линию уровня буквой l. Очевидно, что большим значениям целевой функции соответствуют прямые, параллельные прямой l и сдвинутые относительно неё на "северо-восток".

С учётом сказанного сдвинем прямую  l на "северо-восток" как можно дальше, но так, чтобы получающаяся при этом прямая пересекалась бы с множеством допустимых планов. На рисунке требуемая прямая обозначена буквой L, она пересекается с множеством допустимых планов в точке P. Следовательно, точка P соответствует оптимальному плану рассматриваемой задачи. Из рисунка видно, что координаты точки P суть x₁ = 4, x₂ = 2. Значит, оптимальный план производства заключается в том, что надо произвести 4 единицы продукции первого вида и 2 - второго.

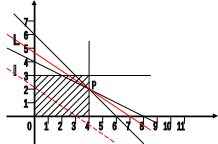
Рис.2.2.1. Геометрическое решение задачи линейного программирования