1. Средняя арифметическая:

а) простая – если исходные данные осредняемого признака представлены в не сгруппированном виде, т.е. как индивидуальные значения первичного признака у отдельных единиц совокупности.

, x_i – индивидуальные значения признака у каждой единицы совокупности, n – число единиц совокупности.

б) взвешенная – применяется если исходные данные сгруппированы и представлены в виде ряда распределения.

, x_i – варианты значений осредняемого признака, f_i – частоты (веса) для каждого из вариантов признака, показывающие их повторяемость, к – число групп.

2. Средняя гармоническая используется в том случае, когда известны варианты значений осредняемого признака (x_i), а также их суммарные результаты M_i = x_i·f_i

простая

взвешенная

3. Средняя геометрическая:

, П – знак произведения.

4. Средняя квадратическая:

простая

взвешенная

5. Мода – величина признака (варианта), которая встречается в ряду распределения или совокупности с наибольшей частотой.

х_mo – нижняя граница модального интервала (это интервал, обладающий наибольшей частотой),

i_mo – величина модального интервала, f_mo – частота модального интервала, f_mo-1 – величина интервала, предшествующего модальному, f_mo+1 – величина интервала следующего за модальным.

6. Медиана – величина признака у единицы совокупности, находящиеся в середине ранжированного (упорядоченного) ряда.

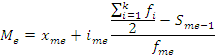
х_me – нижняя граница медианного интервала, i_me – величина медианного интервала, – половина суммы всех частот интервального ряда, S_me-1 – накопленная частота до медианного интервала, f_me – частота медианного интервала.

Правило нахождения накопленных частот:

S₁=f₁; S₂=f₁+f₂; S₃=f₁+f₂+f₃……S_n=f₁+f₂+f₃+…+f_n

Вопрос 9. Мода и медиана: определение, расчетные формулы

Мода – величина признака (варианта), которая встречается в ряду распределения или совокупности с наибольшей частотой. В интервальных вариационных рядах значение моды вычисляется по формуле:

х_mo – нижняя граница модального интервала (это интервал, обладающий наибольшей частотой),

i_mo – величина модального интервала, f_mo – частота модального интервала, f_mo-1 – величина интервала, предшествующего модальному, f_mo+1 – величина интервала следующего за модальным.

Медиана – величина признака у единицы совокупности, находящиеся в середине ранжированного (упорядоченного) ряда.

Если исходные данные представлены в виде интервального ряда распределения с равными интервалами, то для нахождения медианы вначале необходимо найти медианный интервал (это интервал, который содержит единицу совокупности, находящуюся в середине ранжированного ряда).

Для определения этого интервала сумму всех частот ряда делят пополам, а затем путем последовательного накопления (суммирования) частот интервалов, начиная с 1-го, находят интервал, где расположена медианная единица. Медианным будет 1-ый интервал, для которого накопленная частота будет равна или больше половины суммы всех частот. После этого медиану находят по формуле:

х_me – нижняя граница медианного интервала, i_me – величина медианного интервала, – половина суммы всех частот интервального ряда, S_me-1 – накопленная частота до медианного интервала, f_me – частота медианного интервала.

Правило нахождения накопленных частот:

S₁=f₁; S₂=f₁+f₂; S₃=f₁+f₂+f₃……S_n=f₁+f₂+f₃+…+f_n