- •Цифровая обработка данных ср Лекция 1
- •Причины возникновения и особенности цифровой обработки данных сейсморазведки мов огт
- •Основные факторы, влияющие на динамические особенности отраженных волн
- •Математическая модель среды
- •Математическая модель сейсмической трассы
- •Лекция 2 Математическая модель сейсмограммы для однократно отраженных волн
- •Блок-схема математической модели трассы, как канала связи
- •Порядок расчета синтетических трасс или моделирование волновых полей
- •Лекция 3 Динамический диапазон сейсмических колебаний и задачи цифровой автоматической регулировки амплитуд (цара)
- •Восстановление амплитуд и учет неидентичности условий возбуждения и приема
- •Методы изучения скоростей в вчр и порядок расчета СтП в мов огт
- •Понятие компонент ошибок статических поправок
- •Лекция 4
- •Особенности уравнений годографов ошибок СтП, сформированных по опв, опп, огт и общего удаления
- •Этапы коррекции статических поправок
- •Кинематические поправки (nmo)
- •Скорости в сейсморазведке
- •Лекция 5
- •Вертикальный энергоанализ
- •Горизонтальный энергоанализ
- •Коррекция кинематики сканированием скоростей
- •Лекция 6 Миграция. Понятие сейсмического сноса и назначение миграции
- •Назначение процедуры дмо (Dip….MoveOut)
- •Лекция 7
- •Процедуры фильтрации
- •С огласованная фильтрация
- •Временная и амплитудная разрешенность сейсмических записей
- •Лекция 8 Обратная фильтрация (деконволюция)
- •Уравнение Колмогорова-Винера при расчете обратных фильтров
- •Виды обратных фильтров
- •Пространственно-временная фильтрация (fk-фильтрация)
- •Консультация
- •27. Последовательность этапов цо (граф обработки). Задачи препроцессинга и других этапов обработки
- •28. Динамические особенности (атрибуты) сейсмических записей. Понятие пак или сейсмической инверсии.
Виды обратных фильтров
Если соотношение сигнал/помеха сравнительно небольшие, то в этом случае используются фильтры обнаружения сигнала и фильтры воспроизведения сигналов с использованием соответствующих критериев. Если соотношение сигнал/помеха превышает 2,3,5, то в этом случае на основе критерия Винера проводят еще ряд обратных фильтров. Одним из которых является собственно фильтр сжатия, где в качестве желаемого сигнала берут 8.9. Если возбуждение колебаний проводим со взрывами ВВ, то фазовый спектр получаемых сигналов является минимально фазовым. 8.10. Если используются вибраторы, то сигнал получается нуль-фазовый. Если используются материалы взрывной СР, то на начальном этапе обработки, проводят минимально фазовую деконволюцию, т.е. фазовый спектр сигнала берется минимально-фазовым, а на конечных этапах обработки используется нуль-фазовая деконволюция, таким образом, при любых источниках конечные материалы проходят нуль-фазовую деконволюцию, как со взрывными, так и не со взрывными источниками. При одинаковых амплитудо-частотных спектрах сигналы соответствующие нуль-фазовому спектру являются самыми короткими во времени. Кроме того, при нуль-фазовой форме сигнала, у нас при любых преобразованиях сейсмических трасс, основной максимум остается на одном и том же времени, тогда как минимально-фазовый сигнал, может менять свою форму и максимум, по которому мы ведем корреляцию волн, может менять свое t0. Если же взять минимально-фазовый сигнал, то при фильтрации время корреляции t0измениться, что повлечет изменение глубины отражающей границы.
![]()
![]()
![]() - АЧХ фильтра;
- АЧХ фильтра; ![]() – фазово-частотный спектр.
– фазово-частотный спектр.
![]()
![]()
Помимо деконволюции и сжатии часто еще используется обратная фильтрация, называемая «корректирующая». В этом случае проводиться коррекция формы импульса, т.е. мы задаем определенную форму колебаний и все колебания имеют именно эту форму, что повышает эффективность последующего суммирования.
Последний вид – это предсказывающаядеконволюция (или прогностическая), которая чаще всего используется для прогноза появления кратных волн по однократным, которые присутствуют на сейсмограммах и вычитание этих кратных волн из волнового поля. И мы можем сделать такой фильтр, который уберет кратные волны.
Пространственно-временная фильтрация (fk-фильтрация)
Е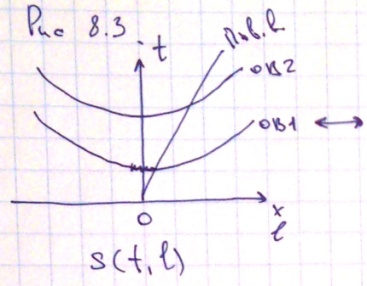
 сли
у нас есть сейсмограмма, рис 8.3, некоторая
функция s(t,l),
которая зависит от времени и пространства
между ПВ и ПП. Если рассчитать прямое
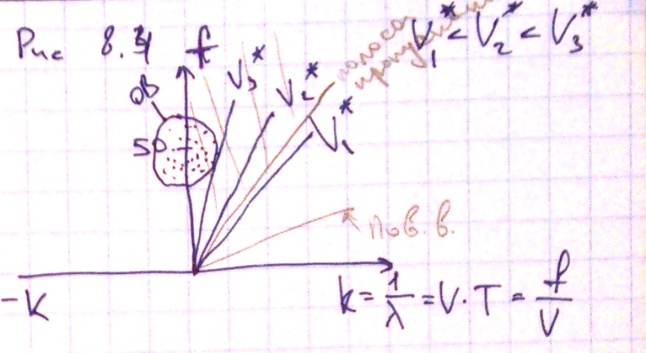
преобразование Фурье, т.е. уйти в
спектральную область, то получим картину
рис 8.4. Причем все прямые линии в
спектральном изображении будут
характеризовать кажущиеся скорости, а
вертикальная ось будет характеризовать
частоту в Гц. Если в плоскости t,l
у нас отраженные и поверхностные волны
попадают в одну область, т.е. годографы
пересекаются, то в частотной области,
они попадают на разные участки F,K
пространства и если задать некоторый
фильтр, который отличается кажущимися
скоростями, то можно избавиться от
поверхностных волн, пропуская при этом
отраженные волны без искажения. Иногда
эти фильтры называются веерными. При
этом необходимо иметь в виду, что
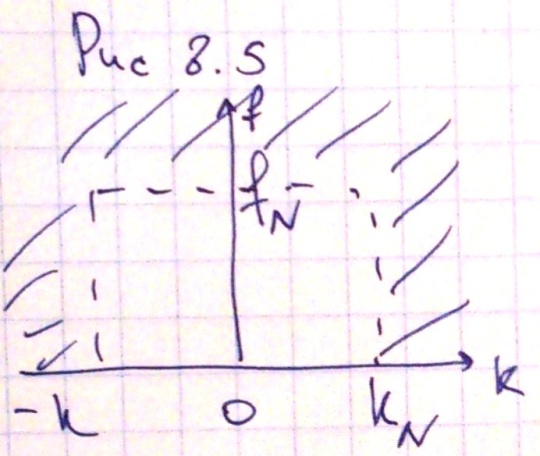
поскольку мы используем дискретное
преобразование Фурье, то при частотах
выше частоты Наикриста, у нас возникают
«зеркальные» или «боковые» частоты, и
в этом случае необходимо вводить
соответствующие ограничения, как по
частоте f,
так и по пространственной частоте k.
Рис 8.5. А наличие информации в заштрихованном
диапазоне, может привести к нелинейным
искажениям соответствующих данных.
сли
у нас есть сейсмограмма, рис 8.3, некоторая
функция s(t,l),
которая зависит от времени и пространства
между ПВ и ПП. Если рассчитать прямое
преобразование Фурье, т.е. уйти в
спектральную область, то получим картину
рис 8.4. Причем все прямые линии в
спектральном изображении будут
характеризовать кажущиеся скорости, а
вертикальная ось будет характеризовать
частоту в Гц. Если в плоскости t,l
у нас отраженные и поверхностные волны
попадают в одну область, т.е. годографы
пересекаются, то в частотной области,
они попадают на разные участки F,K
пространства и если задать некоторый
фильтр, который отличается кажущимися
скоростями, то можно избавиться от
поверхностных волн, пропуская при этом
отраженные волны без искажения. Иногда
эти фильтры называются веерными. При
этом необходимо иметь в виду, что
поскольку мы используем дискретное
преобразование Фурье, то при частотах
выше частоты Наикриста, у нас возникают
«зеркальные» или «боковые» частоты, и
в этом случае необходимо вводить
соответствующие ограничения, как по
частоте f,
так и по пространственной частоте k.
Рис 8.5. А наличие информации в заштрихованном
диапазоне, может привести к нелинейным
искажениям соответствующих данных.