Лекция 8 Обратная фильтрация (деконволюция)

Сейсмическую трассу y(t) можно представить сверткой начального импульса s₀(t) и импульсной реакцией или оператором фильтра h(t), который характеризует воздействие среды на начальный импульс 8.1. или в спектральной области 8.2. Где Y(f) – амплитудо-частотная характеристика сигнала, S(f) – спектр начального сигнала, H(f) –АЧХ среды.

Где y(t) – трасса, q(t) – отраженная волна, n(t) – помехи.

Чтобы найти спектр начального сигнала нужно 8.3. Отсюда следует, что если к спектру сейсмической трассы применить фильтр H’(f), обратный характеристике среды, то мы получим спектр начального сигнала. С другой стороны если взять формулу 8.1. то, чтобы найти s­₀(t) нам нужно сделать процедуру обратную свёртке, т.е. деконволюцию.

П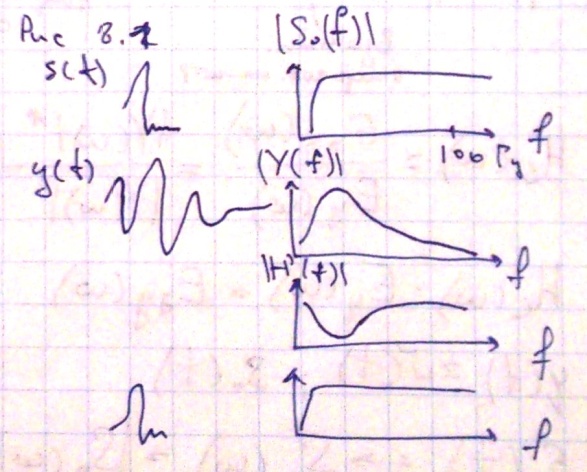 ри возбуждении колебаний у нас возникает сигнал, который считается коротким во времени, но этот сигнал обладает достаточно широким спектром. При распространении импульса в среде он меняется, рис 8.1. При этом с увеличением длительности сигнала, временная разрешающая способность записи уменьшается. Чтобы восстановить форму начального сигнала, нам нужно применить фильтр, частотная характеристика которого является обратной характеристике воздействия среды. Если перемножить эти частотные характеристики, то мы снова получим примерно начальный спектр начального сигнала и соответственно сигнал станет более коротким.

Р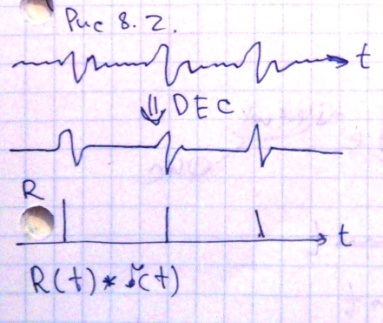 ис 8.2. в идеальном случае мы преобразуем наш начальный сигнал в единичный импульс, или импульс соответствующий коэффициентам отражения. В силу наличия различных помех, такой результат мы получить не можем, но тем не менее мы можем в той или иной степени (в зависимости от соотношения сигнал/помеха) сделать сигнал более коротким или решить ряд других задач.

Уровень соотношения сигнал/помеха и критерии производства оптимальных или обратных фильтрах

При различных соотношениях сигнал/помеха с помощью обратных фильтров мы можем решать различные задачи. Для решения этих задач используются специальные критерии для оптимизации процесса решения задачи. Поэтому такого типа фильтры часто называются оптимальными. Если соотношение сигнал помеха близко к 1, т.е. небольшое, то в этом случае ставится задача обнаружить полезный сигнал на сейсмических записях. В этом случае говорят о фильтрах обнаружения. Для производства фильтрации часто используют критерий максимума пикового отношения сигнала к среднеквадратическому уровню помех. 8.5. – фильтр обнаружения. На практике применяют некоторые вариации фильтров и выбирают такие значения параметров фильтра, чтобы это отношение было максимальным.

Второй критерий, который используется называется критерием Винера, который записывается как 8.6.

Где q_вых(t) – энергия полезного сигнала на выходе фильтра; n_вых(t) – энергия помехи на выходе фильтра; h(t) –оператор фильтра; - трасса после фильтрации; q(t) – желаемый сигнал.

Уравнение Колмогорова-Винера при расчете обратных фильтров

Чтобы выбрать фильтр h(t) часто используется выражение, которое называется уравнением Колмогорова-Винера. Где h(t) – импульсная реакция фильтра, b_y(t) – функция автокорреляции трассы y(t) входной, r_ду(τ) –функция взаимной корреляции трассы и желаемого сигнала q(t).

В частотной области 8.8.

H(ω) –частотная характеристика фильтра, R_ду – взаимный энергетический спектр, B_у(ω) – энергетический спектр, G(ω) – комплексный спектр желаемого сигнала.