§16. Дифференцирование неявных функций.

Опр.1. Функция у от х, определяемая уравнением F (x, y) = 0, называется неявной функцией.

Теорема.

Пусть функция F (x,y) и ее частные производные 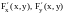определены и непрерывны в окрестности точки (х,у), причем в этой точке . Тогда функция у от х имеет производную

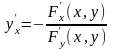
Доказательство.

Выберем некоторое значение х и соответствующее ему значение у. Зададим х приращение Δх, тогда функция y = f (x) получит приращение Δу . При этом F (x,y) = 0,

F (x+ Δx, y+Δy) = 0,

поэтому F (x+ Δx, y+Δy) – F (x,y) = 0.

Слева в этом равенстве стоит полное приращение функции F (x,y), которое можно представить в виде:

.

Разделив обе части полученного равенства на Δх, выразим из него :

.

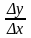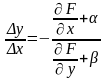В пределе при , учитывая, что 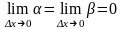и , получим:

,

,

,

.

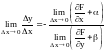Ч.Т.Д.

Пример.

Найт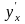и , если .

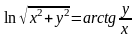Найдем

,

.

Тогда по формуле получаем: .

Для функции определенной неявно соотношением , аналогично получим:

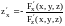и

§17. Уравнения касательной плоскости и нормали к поверхности

Предварительно вспомним известные и выведем новые формулы для касательных и нормалей к плоским и пространственным кривым.

На плоскости:

1. Если кривая задана явной функцией y=f(x), то, уравнение касательной к ней в точке (x₀,y₀) имеет вид:

,

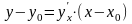а уравнение нормали:

.

2. Если кривая есть график функции, заданной неявно уравнением F(x,y)=0, то, как было показано, , и потому уравнение касательной будет

,

Уравнение нормали:

,

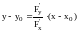3. Если кривая задана параметрически: 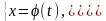, то и уравнение касательной примет вид:

,

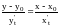
А уравнение нормали:

,

В пространстве:

Опр. 1. Геометрическое место всех возможных касательных называется касательной плоскостью к поверхности в точке P₀.

Опр. 2. Прямая, перпендикулярная касательной плоскости и проходящая через точку P₀, называется нормалью к поверхности в точке P₀.

Уравнение любой плоскости, проходящей через точку P_0, это

A(x-x₀)+ B(y-y₀)+ C(z-z₀) = 0,

где в качестве координат вектора нормали А, В, С берутся величины , , .

Таким образом, уравнение касательной плоскости выглядит как

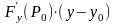+ + =0.

Уравнение нормали запишется, очевидно, в виде

.

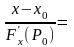
§18. Производная по направлению. Градиент.

Пусть функция u = f (x, y, z) непрерывна в некоторой области D и имеет в этой области непрерывные частные производные. Выберем в рассматриваемой области точку M(x,y,z) и проведем из нее вектор S, направляющие косинусы которого cosα, cosβ, cosγ. На векторе S на расстоянии Δs от его начала найдем точку М₁(х+Δх, у+Δу, z+Δz), где

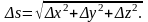
Представим полное приращение функции f в виде:

где

После деления на Δs получаем:

.

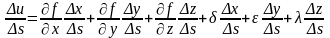Поскольку 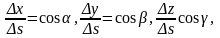предыдущее равенство можно переписать в виде:

(*)

Опр.1. Предел отношения при называется производной от функции u = f (x, y, z) по направлению вектора S и обозначается .

При этом из (*) получаем:

Замечание 1.

Частные производные являются частным случаем производной по направлению. Например, при получаем:

.

Замечание 2.

Выше определялся геометрический смысл частных производных функции двух переменных как угловые коэффициенты касательных к линиям пересечения поверхности, являющейся графиком функции, с плоскостями х = х₀ и у = у₀. Аналогичным образом можно рассматривать производную этой функции по направлению l в точке М(х₀, у₀) как угловой коэффициент линии пересечения данной поверхности и плоскости, проходящей через точку М параллельно оси Oz и прямой l.

Опр.2. Вектор, координатами которого в каждой точке некоторой области являются частные производные функции u = f (x, y, z) в этой точке, называется градиентом функции u = f (x, y, z).

Обозначение: grad u = .
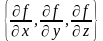