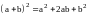Свойства дифференциала
На коллоквиум с доказательством!!!
Доказательство свойств аналогично доказательству свойств дифференциала функции одной переменной.
Дифференцируемость фмп
Опр.4. Если приращение функции z = f (x, y) в точке (x0 , y0) можно представить в виде
,
то функция называется дифференцируемой в этой точке.
А и В не зависят от
и
,
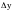но могут зависеть от
и
.
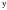Теорема 2. (необходимое условие дифференцируемости ФМП)
Если функция z = f (x, y) дифференцируема в точке (x0 , y0), то в этой точке существуют обе частные производные.
Доказательство:
Как было выведено в доказательстве
Теоремы 1 этого параграфа
и
.
Значит, для существования
необходимо существование частных
производных. Ч.Т.Д.
Теорема 3. (достаточное условие дифференцируемости ФМП)
Если частные производные функции z = f (x, y) непрерывны в точке (x0 , y0), то в этой точке функция дифференцируема.
Доказательство: (самостоятельно, для тех, кто претендует на «5»)
Замечание. Итак, утверждение «функция дифференцируема» не равнозначно утверждению «функция имеет частные производные» - для дифференцируемости требуется еще и непрерывность этих производных в рассматриваемой точке.
Опр.5. Функция, имеющая
непрерывные частные производные в
области
,
называется непрерывно-дифференцируемой
в этой области.
§14. Частные производные высших порядков. Дифференциалы высших порядков.
Частные производные функции z = f (x,y) являются, в свою очередь, функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:
Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д. Определим производные высших порядков так:
Опр. 1. Частной производной n-го порядка функции нескольких переменных называется первая производная от производной (n – 1)-го порядка.
Частные производные обладают важным
свойством: результат дифференцирования
не зависит от порядка дифференцирования
(например,
).
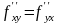Сформулируем это правило в виде теоремы.
Теорема.
Если функция z = f
(x,y)
и ее частные производные
определены и непрерывны в точке
М (х, у) и в некоторой ее окрестности, то в этой точке
.
(Без доказательства)
Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.
.
Дифференциалы высших порядков
Опр. 2. Дифференциалом второго порядка функции z = f (x, y) называется дифференциал от дифференциала первого порядка.
Или
Аналогично, дифференциал третьего порядка равен:
Таким образом можно определить дифференциалы и более высоких порядков.
Опр. 3. Дифференциалом порядка k называется полный дифференциал от дифференциала порядка
(k – 1):
d k u = d (d k-1 u).
Замечание. Дифференциал k-ого порядка является однородным целым многочленом степени k относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные k-го порядка, умноженные на целочисленные постоянные (такие же, как при обычном возведении в степень). Посмотрите на формулы дифференциалов 2 и 3 порядков: они совпадают с формулами
