§6. Квадратурная амплитудная модуляция (кам)

6.1. Математический аппарат модуляции

Любое гармоническое ко­лебание с произвольной фазой можно записать в виде комбинации двух колебаний: по законам функций синуса и ко­синуса. Это следует из следующих тригонометрических ра­венств:

(4.36)

Здесь и - коэффициенты разложения, а и - базисные функции, которые имеют по отношению друг к другу, сдвиг 90, т.е. они находятся в квадратуре. Обычно коле­бание называют синфазной составляющей, а колебание - квадратурной составляющей.

Сущность КАМ заключается в том, что в каждом из квадра­турных каналов производится дискретная амплитудная модуля­ция несущих колебаний и с помощью двух независи­мых модулирующих сигналов. Результирую­щий сигнал представляет собой сумму этих колебаний. Таким образом, два независимых сообщения одновременно будут пере­даваться в одной общей среде.

В общем случае КАМ-сигнал можно представить следующей математической моделью:

(4.37)

где A_c(t) и A_s(t) модулирующие сигналы.

КAМ-сигнал реализуется посредством суммиро­вания двух колебаний, следова­тельно, в одной полосе частот одновременно размещаются два идентичных, но независимых друг от друга ДАМ-сигнaла. Поэтому ширина спектра КАМ равняется ширине спектра одного сиг­нала с дискретной амплитудной модуляцией.

6.2. Структура модулятора и демодулятора

Схема КАМ-модулятора пред­ставлена на рис. 4.21.

Сигналы A_c(t) и A_s(t) подаются на перемножители с опорныни сигналами, находящимися в квадратуре ( и ). В результате на выходе модулятора образуется суммарный КАМ-сигнал.

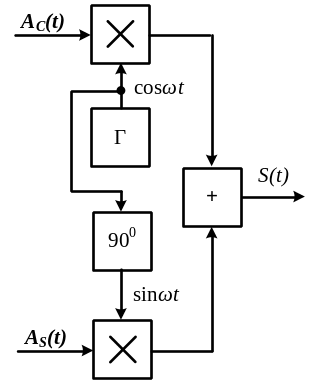
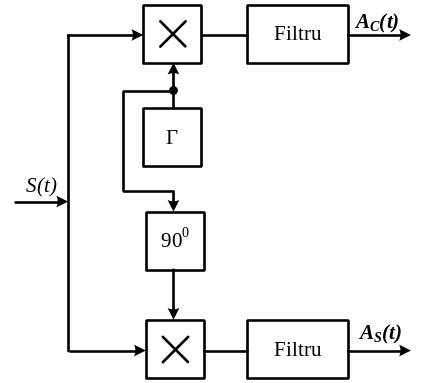
Рис. 4.21 Рис. 4.22

Схема КАМ-демодулятора пред­ставлена на рис. 4.22. Приёмный КАМ сигнал подаётся на два ДАМ-демодулятора с опорными сигналами, находящимися в квадратуре.

§7. Дискретная частотная модуляция (дчм)

7.1. Математический аппарат модуляции

Сигнал дискретной частотной модуляции - в общем случае представляет собой последо­вательность посылок, которые передаются на различных частотах. ДЧМ-сигнал можно представить выражением:

(4.38)

где A(t) – модулирующий сигнал, - девиация частоты.

В частном случае, когда A(t) двоичный сигнал, ДЧМ-сигнал можно записать в следующем виде:

(4.39)

Девиационная частота в этом случае:

(4.40)

Временная диаграмма этого сигнала пред­ставлена на рис. 4.23

Рис. 4.23

Дискретная частотная модуляция характеризуется еще одним параметром - индексом частотной модуляции m_f:

(4.41)

где , T – длительность посылки сигнала.

7.2. Спектр дчм-сигнала

Спектр сигнала с дискретной частотной модуляцией при M=2 и индексе модуляции m_f=2 пред­ставлен на рис. 4.24.

Анализируя спектр ДЧM-сигнала, можно отметить следую­щее:

• с увеличением индекса частотной модуляции m_f амплитуда несущего колебания уменьшается;

• при индексе модуляции, близком к единице (m_f≈1), основ­ная часть мощности сигнала заключена в несущей частоте и бо­ковых составляющих на частотах ω₀+Ω и ω₀-Ω.

• ширина спектра ДЧМ-сигнала примерно в два раза превышает ширину спектров сигналов ДАМ и ДФМ.

Рис. 4.24