Глава IV. Методы модуляции в системах передачи информации

§1. Классификация методов модуляции

Модуляция - это процесс преобразования информационного сигнала в высокочастотный сигнал с целью передачи его на большие расстояния.

В процессе модуляции участвуют следующие сигналы:

- модулирующий сигнал A(t), содержащий передаваемое сообщение;

- несущий сигнал x(t) на который переносится модулирующий сигнал;

- модулированный сигнал S(t) как результат воздействия модулирующего сигнала на несущий.

По виду передаваемого сообщения различают два вида модуляций:

• Аналоговая модуляция если A(t) непрерывный сигнал

• Дискретная модуляция если A(t) цифровой сигнал

По виду несущего колебания x(t) различают два вида модуляций:

- модуляция с синусоидальной (гармонической) несущей;

- модуляция с импульсной несущей.

Аналоговая модуляция с синусоидальной несущей, в зависимости от модулирующего параметра может быть:

- амплитудная модуляция;

- частотная модуляция;

- фазовая модуляция.

Частотные и фазовые модуляции называются угловыми модуляциями.

Дискретная модуляция с синусоидальной несущей, в зависимости от модулирующего параметра может быть:

• дискретная амплитудная модуляция (ДАМ):

• дискретная фазовая модуляция (ДФМ);

• квадратурная амплитудная модуляция (КАМ);

• амплитудно-фазовая модуляция (АФМ);

• дискретно-частотная модуляция (ДЧМ);

• дискретно-частотная модуляция с непрерывной фазой (ДЧМНФ);

• дискретно-частотная модуляция с минимальным сдвигом (ММС).

Модуляция с импульсной несущей, в зависимости от модулирующего параметра может быть:

• амплитудно-импульсная модуляция (АИМ).

• широтно-импульсная модуляция (ШИМ),

• временная импульсная модуляция (ВИМ).

§2. Аналоговая амплитудная модуляция

2.1. Математический аппарат модуляций

Амплитудной модуляцией (АМ) называется изменение амплитуды несущего сигнала x(t) в соответствии с модулированным колебанием A(t). В этом случае сигналы A(t) и x(t) имеют вид:

(4.1)

(4.2)

где: U_Ω – амплитуда модулирующего сигнала

Ω – частота модулирующего сигнала

U_m – амплитуда несущего сигнала

ω – частота несущего сигнала и ω>> Ω.

Рис. 4.1.

Модулированный сигнал S(t) имеет вид:

(4.3)

Временные диаграммы, иллюстрирующие процесс амплитуд­ной моцуляции, показаны на рис. 4.1.

Коэффициентом модуляции m называется отношение амплиту­ды модулирующего сигнала U_Ω к амплитуде несущего колебания U_m.

(4.4)

2.2. Спектр ам сигнала

Из выражений (4.4) и (4.3) следует:

(4.5)

Раскроем выражение (4.5), что позволит определить спектр АМ-сигнала:

(4.6)

Из этого выражения видно, что АМ-сигнал, спектр кото­рого при модуляции одним гармоническим сигналом изображен на рис. 4.2, содержит три составляющие:

• колебание несущей частоты ω и амплитудой U_m

• колебания верхней боковой частоты ω+Ω с амплитудой

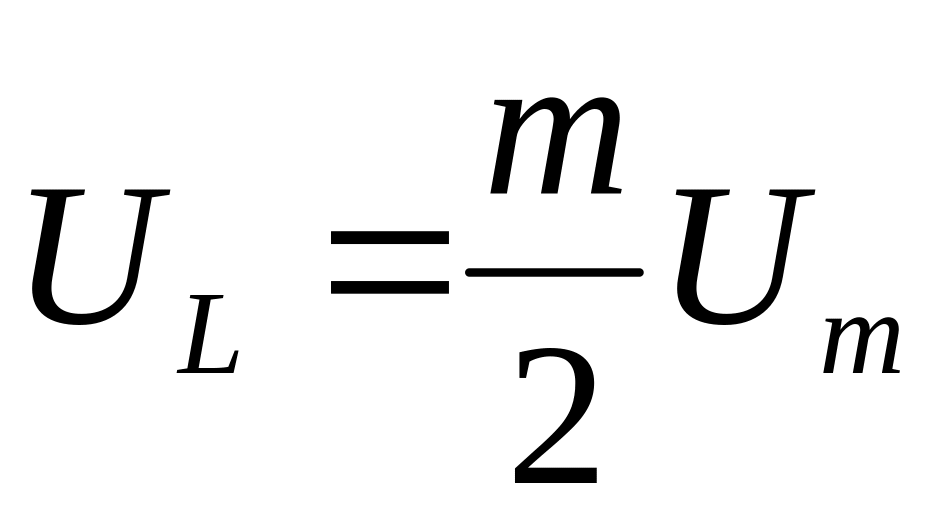
• колебания нижней боковой частоты ω-Ω с амплитудой

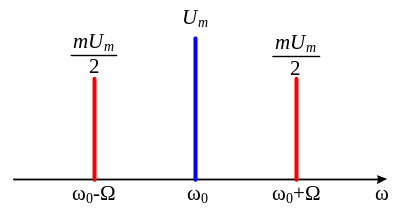
Рис. 4.2

Из сказанного можно сделать следующие выводы:

• Ширина спектра равна удвоенной частоте модуляции,

(4.7)

• Амплитуда несущего колебания при модуляции не изменя­ется, а амплитуды колебаний боковых частот пропорциональны амплитуде модулирующего сигнала.

• При m=1 амплитуды колебаний боковых частот равны по­ловине амплитуды несущего колебания. При m=0 бо­ковые частоты отсутствуют, что соответствует немодулированно­му колебанию.

На практике одночастотные АМ-сигналы используются край­не редко. Обычно, модулирующий сигнал имеет сложный спектральный состав. В этом случае в спектре АМ-сигнала кроме несущего ко­лебания содержатся группы верхних и нижних боковых колеба­ний (рис. 4.3).

Рис. 4.3.

Средняя мощность несущей частоты:

(4.8)

а каждая из боковых составляющих имеет мощность:

(4.9)

В этом случае средняя мощность всего АМ-сигнала есть сумма мощностей несущей частоты и двух боковых частот - нижней и верхней:

(4.10)

Из этой формулы видно, что при 100%-й модуляции 66,6% всей мощности, затрачивается на пе­редачу несущей частоты и только 33,3% мощности приходится на оба колебания боковых частот, которые как раз и содержат по­лезную информацию.