Вопрос 78. Явная и неявная двухслойная четырехточечная разностная схема для уравнения теплопроводности, условия устойчивости.

Запишем уравнение теплопроводности:

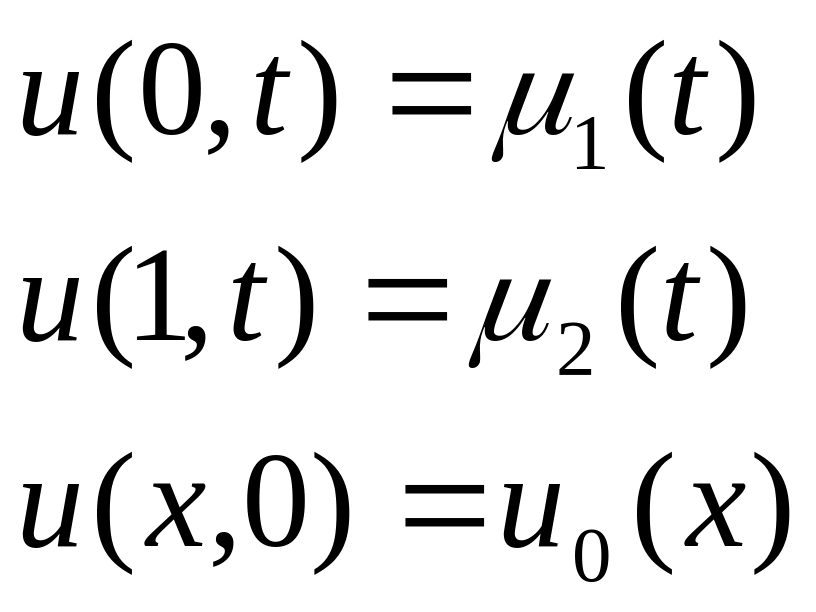
u=u(x,t)

0<x<1

0<t<T

1. Явная двухслойная четырехточечная схема.

Введем шаблон

Заменим дифференциальную задачу разностной.

Имеем:

Исследуем на устойчивость данную разностную задачу. Сначала исследуем на устойчивость по начальным данным:

подставляем в уравнение, сократив имеем

, где

=>

Для того чтобы разностная схема сходилась по начальным данным достаточно чтобы

В данном случае должно выполнятся следующее:

Таким образом данная разностная схема устойчива по начальным данным с условием

Теперь исследуем устойчивость по правой части:

Сделаем оценку.

Было преобразуем и оценим

, 1-2r>0

Так как

,то

.

А это и есть определение устойчивости по правой части, то есть схема устойчива по правой части при .

Таким образом данная разностная схема будет условно устойчива с условием , так как она устойчива по начальным данным и по правой части.

2. Неявная двухслойная четырехточечная схема.

Введем шаблон:

Заменим дифференциальную задачу разностной.Имеем:

Исследуем на устойчивость данную разностную задачу. Сначала исследуем на устойчивость по начальным данным:

подставляем в уравнение сократив, имеем

где

=>

Для того чтобы разностная схема сходилась по начальным данным достаточно чтобы или

В данном случае должно выполнятся следующее А это условие выполняется всегда => таким образом данная разностная схема будет устойчива по начальным данным. Теперь исследуем устойчивость по правой части

Сделаем оценку

Было преобразуем и оценим

, 1+2r>0

Таким образом

Так как , то

.

А это и есть определение устойчивости по правой части, то есть схема устойчива по правой части.

Таким образом данная разностная схема будет безусловно устойчива, так как она устойчива по начальным данным и по правой части.