11. Электростатическое поле в диэлектриках.
Представим диэлектрик как систему диполей. Во внешнем поле диэлектрик поляризуется, т. е. диполи из которых состоит диэлектрик поворачиваются и ориентируются вдоль линий напряженности электрического поля.
На краях диэлектрика скапливаются отрицательные и положительные заряды, поле создаваемое диполями противоположно внешнему полю, и поэтому напряженность поля внутри диэлектрика меньше чем снаружи.
Чтобы математически описать плотность поляризованных зарядов, возникающую, при смещении зарядов используем закон сохранения заряда.
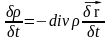
Результирующее
плотность поляризованного заряда в
веществе возникает в результате смещения
положительных и отрицательных зарядов.
Будем считать, что плотности поляризованных
отрицательных и положительных зарядов
приблизительно
равны. Тогда плотность поляризованного
заряда равна
- плотность связанных
зарядов
-поляризованность
вещества
-поляризованность
(плотность дипольного момента
вещества). С другой стороны поляризованность вещества можно представить как плотность дипольного момента вещества.
-
дипольные моменты.
Электрическое поле Е внутри диэлектрика создается как свободными зарядами так и связанными зарядами, поэтому внутри диэлектрика теорема Гаусса записывается следующим образом
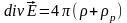
Введем обозначение
-вектор электрической индукции. Этот
вектор может быть интерпретирован как
напряженность электрического поля
создаваемая свободными зарядами в
вакууме.
-теорема Гаусса
для диэлектрика
В общем случае
может
очень сложно завесить от Е. Однако, для
большинства диэлектриков при не слишком
больших напряженностях электрического
поля это зависимость линейная
где η -диэлектрическая
восприимчивость
- диэлектрическая
проницаемость
Для большинства
диэлектриков
.
Следовательно, напряженность поля,
создаваемая зарядом e
в диэлектрике в
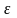меньше напряженности поля.
12 Теорема Гаусса и ее применение к решению задач. Поле бесконечной однородно заряженной плоскости
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:
где dq – заряд, сосредоточенный на площади dS; dS – физически бесконечно малый участок поверхности.
Пусть
σ во всех точках плоскости S
одинакова. Заряд q
– положительный. Напряженность
во
всех точках будет иметь направление,
перпендикулярное плоскости S
(рис. 2.11).
Очевидно, что в симметричных, относительно плоскости точках, напряженность будетодинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).
|
|
|
||
|
Рис. 2.11 |
Рис. 2.12 |
|
|
Тогда
Применим
теорему Остроградского-Гаусса. Поток
ФЕ
через боковую
часть поверхности цилиндра равен нулю,
т.к.
Дляоснования
цилиндра
Суммарный поток через замкнутую поверхность (цилиндр) будет равен:
Внутри
поверхности заключен заряд
.
Следовательно, из теоремы Остроградского–Гаусса
получим:
;
откуда видно, что напряженность поля плоскости S равна:
|
|
(2.5.1) |
|
Полученный
результат не зависит от длины цилиндра.
Это значит, что на любом расстоянии от
плоскости
с обзорки
Рассмотрим
бесконечную заряженную поверхность с
поверхностной плотностью зарядов
Используем терему Гаусса в интегральной форме
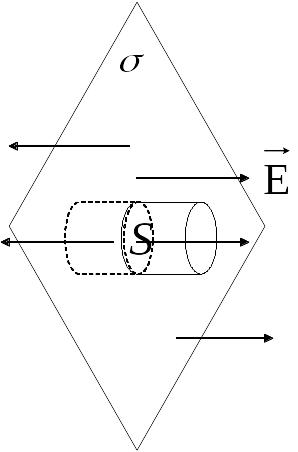
Поток вектора через поверхность цилиндра равен сумме потоков через основание и боковую поверхность цилиндра.
Вектор напряженности электрического поля E направлен перпендикулярно к заряженной поверхности поэтому поток через боковую поверхность цилиндра равен нулю.
Напряженность поля бесконечно заряженной плоскости не зависит
от расстояния, а зависит только от .
Найдем напряженность поля создаваемую заряженным диэлектрическим шаром.
1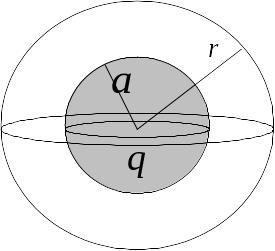
)
Сначала рассмотрим случай когда
.
Вокруг заряженного шара построим
воображаемую сферу, через которую
найдем поток напряженности
электрического поля. Используя теорему Гаусса в
дифференциальной форме получим
,
т.е напряженность поля заряженного
шара выражается такой же формулой как
и для точечного заряда.
2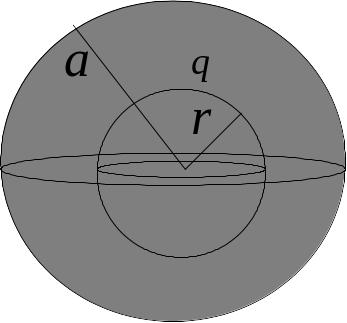
)
Если
то, используя теорему
Гаусса получим
,
где V-
это обьем
воображаемой сферы
Отсюда получим, что напряженность поля внутри заряженного шара равна
