5,6. Энергия электростатического поля. Энергия системы покоящихся зарядов.
Рассмотрим
произвольную ограниченную систему
зарядов находящихся диэлектрической
среде. Выделим произвольную область
содержащую систему зарядов и ограниченную
замкнутой поверхностью S.
Энергия электростатического поля,
содержащаяся в V0
равна
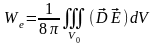
Пологая
и интегрируя по частям, находим
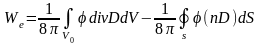(19.1)
Будем считать
поверхность S
сферой бесконечно большого радиуса R.
Тогда при
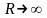потенциал
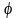убывает
как
,
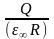где
-
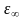диэлектрическая проницаемость среды
на бесконечности, а
-
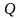полный свободный заряд системы, равный
по теореме Гаусса
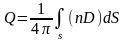
Все это позволяет получить следующую оценку для поверхностного интеграла (19.1):
Так как потенциал убывает обратно пропорционально расстоянию то при
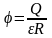
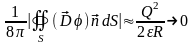
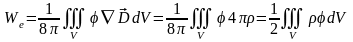(19.2)
где
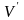-область
занятое свободными зарядами.
Учтем теперь, что
потенциал
удовлетворяет
уравнению Пуассона
и поэтому может быть записан в форме
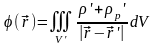(19.3)
где - область, занятая свободными и связанными зарядами. Подставляя (19.3) в (19.2), получаем выражение для энергии электростатического поля в среде:
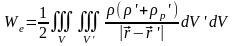
обычно используемое
симметричное выражение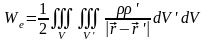
(19.4)
Если заряды считать точечными, то (19. 4) будет содержать расходящиеся интегралы, отвечающие собственным энергиям отдельных зарядов. Если заряд е равномерно распределен по поверхности шарика радиуса а, то энергия электростатического поля, равна
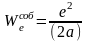
и при
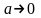оказывается
бесконечной.
Энергия системы
точечных зарядов будет равна, здесь
-
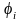потенциал создаваемый всеми зарядами
кроме i-го.
7-8 вопрос потенциальный характер.связь потенциала
Из обзорных лекций
Потенциал электростатического поля. Поле консервативной силы может быть описано не только векторной функцией, но эквивалентное описание этого поля можно получить, определив в каждой его точке подходящую скалярную величину. Для электростатического поля такой величиной является потенциал электростатического поля, определяемый как отношение потенциальной энергии пробного заряда q к величине этого заряда, j = Wп / q, откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит Вольт (1 В).
Потенциал поля точечного заряда Q в однородной изотропной среде с диэлектрической проницаемостью e :
.
|
Для установления
связи между силовой характеристикой
электрического поля -
напряжённостью
и его
энергетической характеристикой -
потенциалом
рассмотрим элементарную работу сил
электрического поля на бесконечно
малом перемещении точечного заряда
q:
dA = q E
dl,
эта же работа равна убыли потенциальной
энергии заряда q:
dA = -
dWп
= -
q d Ex dx + Ey dy + Ez dz = -d , (1.8) где Ex, Ey, Ez - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем
откуда
Стоящее в скобках выражение является градиентом потенциала j, т. е. E = - grad = -Ñ . Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала. Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 4pe0er. Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора
Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна
т. е. в этом направлении потенциал электрического поля является постоянной величиной ( = const).
В рассмотренном
случае направление вектора r
совпадает
с направлением силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.
При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми. Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.
|
|
,
где d
- изменение потенциала электрического
поля на длине перемещения dl.
Приравнивая правые части выражений,
получаем: E
dl
=
-d
или в декартовой системе координат
.
.
,
рис.
1.6
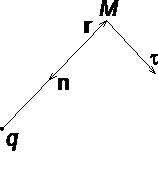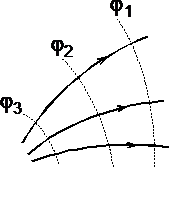рис.
1.7