3. Плотность заряда и плотность тока.
В макроскопической
теории отношение
является
вполне определенной функцией точки r
и называется плотностью
электрического заряда
.
Таким образом,
При этом заряд в произвольной области V представляется в виде
Введем теперь еще
одно важное понятие - плотности
электрического тока j.
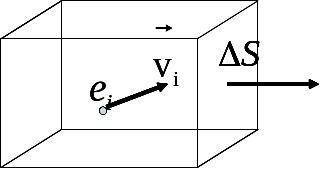
Для этого
рассмотрим площадку
с
нормалью n
(рис.
2.1) и
подчитаем заряд
,
пересекший ее за промежуток времени
.
Выделим сначала заряды еi,
имеющие
скорости
,
лежащие в некотором интервале
со
средней скоростью V.
Тогда все такие заряды, находящиеся в
объеме призмы с высотой
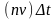и основанием
,
пройдут за время
через
площадку
.
Учитывая, что плотность выделенных
электрических зарядов равна
,
находим заряд, пересекший площадку Рис. 2.1
за отрезок времени со средней скоростью v:
Теперь, чтобы найти
полный заряд
,
достаточно лишь просуммировать
по
всем возможным интервалам
:
где введена плотность электрического тока
(2.1)
Общее определение
ПЛО́ТНОСТЬ ТО́КА, векторная характеристика электрического тока j, равная по модулю электрическому заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению упорядоченного движения заряженных частиц.
При равномерном распределении плотности электрического тока по сечению проводника плотность тока j будет равна отношению силы тока I в нем к площади его поперечного сечения S:
j = I/ S
Плотность тока характеризует силу тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока
Единицей измерения плотности тока является А/м2.
Плотность тока можно определить также следующим образом:
Так как сила тока I = nevS, где:
n — концентрация носителей заряда;
e — заряд носителей тока;
v — средняя скорость упорядоченного движения частиц;
S — площадь поперечного сечения проводника, через который течет ток,
То плотность тока J = I/ S = nev S/ S = nev.
Произведение ne характеризует плотность заряда е (заряд в единице объема), поэтому плотность электрического тока:
j =rеv.
Плотность тока величина векторная, по направлению совпадает с направлением вектора скорости v, т. е. с направлением упорядоченного движения электрических зарядов.
Плотность тока пропорциональна вектору напряженности:
j = sЕ.
Коэффициент пропорциональности — проводимость вещества проводника .
Плотность тока более фундаментальная характеристика, чем сила тока, так как дает информацию о распределении течения заряда по проводнику.
4. Закон сохранения заряда.
Зако́н сохране́ния
электри́ческого заря́да
гласит, что алгебраическая сумма зарядов
электрически замкнутой системы
сохраняется.Закон сохранения заряда
выполняется абсолютно точно.
Запишем
закон сохранения электрического заряда
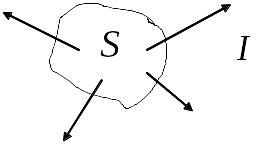
для некоторого объема V,
окруженного замкнутой поверхностью S
(рис. 2.2).
В этом случае (3*) и теорема Гаусса-
Остроградского дают
.
Рис. 2.2
В предположении, что поверхность S не изменяется со временем, примет вид
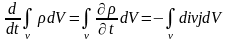
Так как объем V выбран произвольно, то
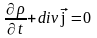
Так выражается закон сохранения электрического заряда в дифференциальной форме.
Сохраняя обозначения
и
для
плотностей свободных зарядов и токов,
полные плотности, очевидно, можно
представить в виде
В большинстве электродинамических задач предполагается, что закон сохранения имеет место, как для свободных, так и для связанных зарядов в отдельности, т. е. исключаются процессы перехода связанных зарядов в свободные и обратно. Поэтому разумно принять, что
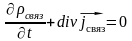
Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
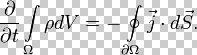
Здесь Ω — некоторая произвольная область в трёхмерном пространстве,dΩ — граница этой области, p — плотность заряда, j— плотность тока (плотность потока электрического заряда) через границу.Закон сохранения заряда в дифференциальной формеПереходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)
