25. Способы построения начального опорного плана тз (Наименьшего Эл-та, северо-западного угла, Фогеля)

Опорный план можно построить несколькими способами.

Правило «северо-западного угла». Суть состоит в том, что первой загружается левая верхняя клетка (1.1). а затем двигаемся от нее по строке вправо или по столбцу вниз. В клетку (1.1) занесем меньшее из чисел а1, в1. Если закрывается строка, то следующей загружается клетка (2.1); если же закрывается столбец, то следующей загружается клетка (1.2). Итак, каждый раз загружается клетка, соседняя либо по строке, либо по столбцу. Последней будет загружена клетка (m;n). В результате загруженные клетки расположатся вдоль диагонали (1;1) – (m;n), поэтому способ «северо-западного угла» называют еще диагональным способом.

Способ «минимального элемента». Суть: первой в таблице загружается клетка с наименьшим тарифом. В клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответств-ю поставщику, запасы которого полностью израсходованы, или столбец, соответств-й потребителю, спрос которого полностью удовлетворен. Из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. В результате получаем опорный план, который должен содержать m+n-1 загруженых клеток. В процессе заполнения таблицы могут быть одновременно исключены строка или столбец. Так бывает, когда полностью исчерпывается запас груза и полностью удовлетворяется спрос ( вырожденная задача). В этом случае в свободные клетки надо записать число 0 – «нуль-загрузку», условно считая такую клетку занятой. Однако число 0 записывается в те свободные клетки, к-рые не образуют циклов с ранее занятыми клетками.

Метод «Фогеля». Суть: по строкам и столбцам определяется разность между двумя наименьшими тарифами. Из этих разностей выбирается наибольшая и в соответствующей строке (столбце) загружется клетка с наименьшим тарифом. Закрывающаяся строка (столбец) исключ-ся из дальнейшего рассмотрения. Описанная операция повторяется m+n-1 раз. Если наибольшая разность окаж-ся сразу в нескольких строках (столбцах), то выбир-т ту строку (столбец), в к-рой придется загружать клетку с наименьшим тарифом. Если и эти показатели будут одинаковы, то выбирают клетку, в к-рую придется записать большую поставку.

26, 27, 28. Признак оптим-ти опорного плана. Оценка свободной клетки трансп.Таблицы. Процедура преобраз-я опорного плана тз в новый опорный план.

В соответствии с теорией двойственности, если xij*=0, то ui+vj<=cij, т.е.разность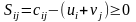

- наз-ся оценкой свободной клетки и ее величина показ-т, как измен-ся общая ст-ть перевозок, если по маршруту (ij) провести единицу груза. Таким образом признаком оптимальности опорного плана ТЗ является неотрицательность оценок свобод.клеток. если среди оценок есть отриц-ые, то чтобы уменьшить общую ст-ть перевозов нужно загрузить первую очередь клетку с наибольшей по модулю отрицательной оценкой. Такую клетку наз-ют перспективной. Если в распределит-ой таблице, содержащей оптим.план, имеются свободные клетки с нулевыми оценками, то задача имеет не единственный оптим.план. Загружая свободную клетку с нулевой оценкой, можно найти еще один оптим.опорный план. И так для каждой свободной клетки с нулевой оценкой.

Чтобы осуществить переход от одного опорного плана к другому необходимо загрузить перспективную клетку. Для этой клетки составляется цикл. Нужно доказать, что для каждой свободной клетки трансп.таблицы, содержащей опорный план, сущ-ет цикл, причем только единственный. Вершины цикла помечаются знаками «+» и «-» поочередно, начиная со свободной клетки. Далее выбир-ся наименьшая из загрузок клеток, отмеченная «-». Она обозначается число λ добавляется к загрузке клеток, помеченных «+», и вычитается из загрузки клеток, отмеченных «-». Клетка по к-рой выбрано число λ освобождается. Если освобождается одновременно несколько клеток, то свободной остается та, в к-рой наибольший тариф. В остальные освободившиеся вписывается загрузка 0.