2.2. Основные параметры и зависимости теоретических лопастных машин

Под теоретической понимается машина, рассеивание энергии которой отсутствует. Подача, напор, давление лопастных машин в решающей степени зависят от изменения жидкости в рабочем колесе. Будем рассматривать установившееся движение. Для идеальной машины рабочее колесо имеет бесконечное число лопаток, а движение потока между ними считается ламинарным. Каждая частица потока имеет два направления движения: вместе с вращением колеса по касательной к мгновенному радиусу и относительно лопатки от центра к периферии. Мгновенные скорости называются окружными (переносными) – U и относительными – W, а их геометрические суммы – абсолютными скоростями  + 

Для определения основных параметров машины достаточно знать скорости на входе (им приписывают индекс 1) и выходе (индекс 2) из рабочего колеса.

Окружная скорость на выходе из колеса U₂ = R (где R – радиус колеса), а на выходе U₁ = r (где r – радиус входа в межлопастной канал;  – угловая скорость).

Рис.17. Планы скоростей на входной и выходной кромках рабочего колеса центробежного насоса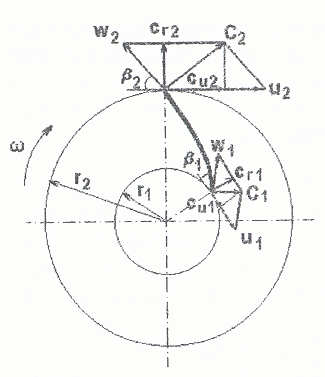

Относительные скорости зависят от подачи машины и при большем числе лопаток имеют направление близкое к касательной к ним (рис.17). На рис.17 С_U1, C_U2 – проекции абсолютных скоростей на окружные; С_r1, C_r2 – составляющие абсолютных скоростей на радиальные направления; ₁, ₂ – углы между векторами абсолютных и окружных скоростей; ₁, ₂ – углы между направлениями относительных и продолжениями окружных скоростей. Конструкции современных центробежных насосов выполнены таким образом, что проекция С_U1 = 0, т.е. имеет место радиальный вход потока на рабочее колесо за счет установки направляющего аппарата.

Теоретическая подача – количество жидкости, перемещаемое в единицу времени без учета утечек, или расход через любое сечение потока. Контрольным принимается сечение на выходе из колеса. Для радиальной машины это сечение равно площади боковой поверхности цилиндра за вычетом площади сечения выходных кромок лопаток

S = D₂b₂ – b₂lz', (17)

где D₂ – диаметр колеса; b₂ – его ширина; l – длина косого среза лопатки; z' – число лопаток.

Если площадь контрольного сечения умножить на нормальную к нему составляющую скорости С_r2, то получим теоретический расход

Q_т = K_cD₂b₂C_r2, (18)

где – коэффициент стеснения потока лопатками.

Для осевой машины сечение на выходе из рабочего колеса

,

где D – внешний диаметр колеса; d – диаметр втулки.

Рис.18. Рабочее колесо турбомашины (а), параллелограммы скоростей, усилия, действующие на элемент лопатки (б), график определения скорости W_m (в)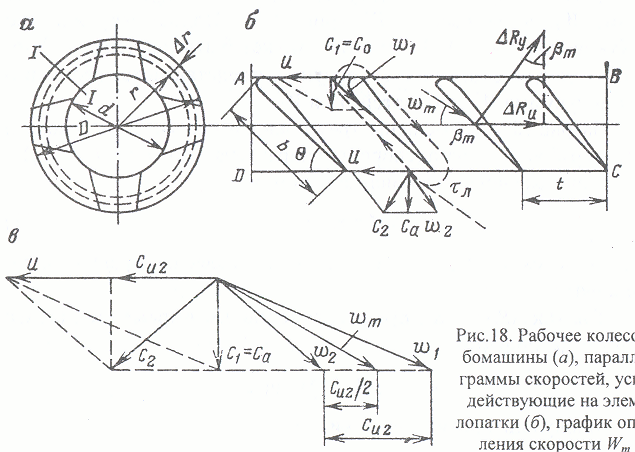

Выходные кромки делаются острыми и поэтому не стесняют поток. Скорость в данном сечении может быть получена из плана скоростей на рис.18 (С_а – проекция абсолютной скорости на нормаль к сечению колеса). Отсюда

. (19)

В теоретической машине вся энергия, подводимая к валу, передается потоку.

Мощность, подводимая к колесу от двигателя, N = M, где М – момент вращения;  – угловая скорость колеса.

Мощность потока N_n = P_т Q_т, где Р_т – теоретическое давление машины. Так как в теоретической машине N = N_п, то .

Выделим на рабочем колесе кольцевой элемент радиусом r (рис.18, а), расход через выделенный элемент составит

Q_т = 2rrC_a,

а мощность, передаваемая потоку будет равна N = M, тогда

(20)

При обтекании единичного профиля потоком идеальной жидкости на него действует подъемная сила R_{y ,}направленная перпендикулярно к вектору скорости _, относительной к крылу (рис.18, б).

В нашем случае относительный поток на выходе крыла имеет значение W₁, а на выходе W₂ (рис.18, б). Подъемная сила (по Н.Е.Жуковскому и С.А.Чаплыгину) может быть найдена по формуле (15), только в качестве скорости _ представляется геометрическая полусумма W_m cкоростей W₁ и W₂.

На рис.18, в совмещены треугольники скоростей на входе и выходе из рабочего колеса (скорость направлена по оси, т.е. С₁ = С_а).

В выражении (20) элементарный момент

M = rzR_U, (21)

где R_U – проекция подъемной силы на направление вращения; z – число лопаток.

Так как R_U = R_ysin_m , то, заменив R_y выражением (15), с учетом l = r, получим

R_U = W_mГ_лrsin_m,

где Г_л – циркуляция вокруг лопатки.

Учитывая, что W_msin_m = C_a, а Г = zГ_л (для z лопаток) из (21) получим

  rC_arГ (22)

и подставив в (20), найдем

. (23)

Для определения циркуляции Г выделим на рис.18, б контур АВСДА, охватывающий циркуляционные потоки, создаваемые всеми лопатками.

Итак, Г_АВСДА = Г = Г_АВ + Г_ВС + Г_СД + Г_ДА, но ВС и ДА – одна линия (линия разреза колеса), поэтому Г_ВС = –Г_ДА. Тогда циркуляция на входе в рабочее колесо Г₁ = Г_АВ = 2rC_U1, а в потоке за колесом Г₂ = Г_СД = 2rC_U2. Знак () следует из того, что поток на входе в рабочее колесо может быть закручен по направлению вращения или против, т.е. С_U1 больше или меньше нуля. Таким образом

Г = 2r(C_U2  С_U1). (24)

Подставив (24) в (23) с учетом r  U, получим

P_т = U(C_U2  С_U1). (25)

Для перехода к напору разделим (25) на g, тогда

H_т =  (C_U2  С_U1). (26)

Сущность рабочего процесса лопастной машины состоит в передаче энергии потоку при силовом воздействии лопаток на поток с закручиванием потока.

Для центробежной машины характерны аналогичные процессы возникновения циркуляции вокруг лопаток. Накладываясь на основной (транзитный) поток (рис.19), циркуляционный поток создает разные скорости на передней и задней сторонах лопатки, что обуславливает разницу давлений в межлопаточном пространстве. За счет этого и происходит передача энергии.

Рис.19. Схема циркуляции

в центробежном колесе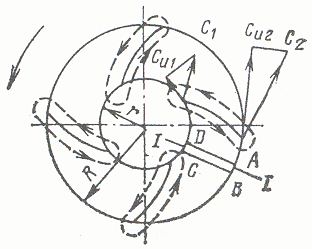

Условно разрежем колесо сечением I–I (рис.19) и разогнем его так, чтобы образовался зазор с контуром АВСДА, который охватит все лопатки. Циркуляция, создаваемая колесом, Г = Г_АВСДА = Г_АВ + + Г_ВС + Г_СД + Г_ДА. Так как Г_ВС = = –Г_ДА; Г_АВ = 2RC_U2 и Г_СД = = 2rC_U1, то Г = 2(RC_U2  rC_U1), получим

P_т = (U₂C_U2  U₁C_U1), (27)

где U₂ = R и U₁ = r.

Разделив уравнение (27) на g, получим выражение для напора

H_т =  (U₂C_U2  U₁C_U1). (28)

Это выражение было впервые получено Л.Эйлером и называется основным уравнением турбомашины.

Вывод теоретической характеристики лопастной машины. Предпосылкой, из которой исходил Л.Эйлер, послужило предположение о бесконечном числе лопаток колеса, поток между которыми носит струйный характер и повторяет форму лопаток. В результате уравнение (28) было получено в виде

H_т =  ( U₂C_U2  U₁C_U1). (29)

Обратимся к рис.17. При использовании направляющего аппарата на входе в колесо скорость закручивания потока сил может оказаться равной нулю, тогда

H_т =  U₂C_U2 или H_т =  U₂C_U2, (30)

а коэффициент циркуляции

,

для различных конструкций колес K_ц = 0,7-0,9 [3].

При радиальном входе потока на рабочее колесо (C_U1 = 0) напор Н_т определяется по формуле (30). Выразим скорость C_U2 через подачу Q_т (рис.20):

C_U2 = U₂ – C_r2ctg₂,

где ₂ – угол выхода лопаток из рабочего колеса.

Рис.20. Теоретические характеристики турбомашин: а – определение коэффициента циркуляции; б,в,г – влияние угла выхода лопаток на скорость закручивания H_CU2; д – зависимость теоретического напора от теоретической подачи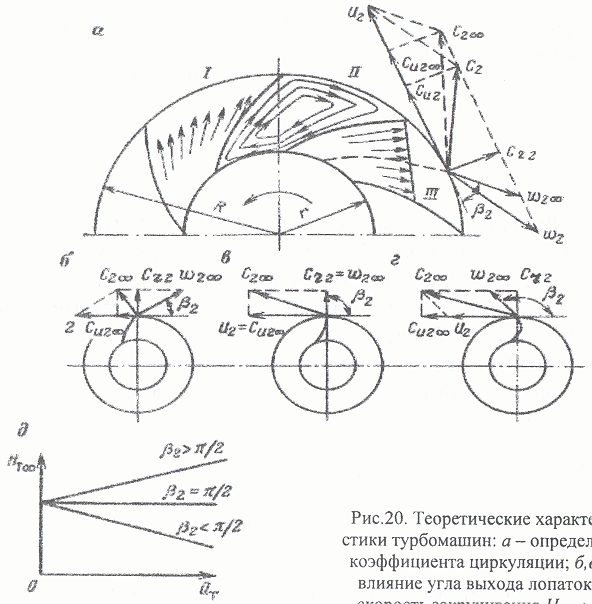

Из выражения (18) имеем С_r2 = Q_т/(K_сD₂b₂). Использовав зависимость (30), получим

Так как Н_т = K_цН_т , то получим окончательно уравнение напорной характеристики теоретической лопастной машины:

(31)

Отсюда видно, что при K_c = const и U₂ = const зависимость H_т = f(Q_т) будет линейной. Начальная ордината этой зависимости есть напор при Q_т = 0.

Если U₂ = D₂n/60 (где n –частота вращения колеса, об/мин), то

, (32)

т.е. Н_т = А – ВQ_т.

Рабочие колеса центробежных машин в зависимости от угла выхода лопаток ₂ могут быть разделены на три группы: колеса с лопатками, загнутыми назад – _   (рис.20, б); колеса с радиальными лопатками – _ =  (рис.20, в); колеса с лопатками, загнутыми вперед – _   (рис.20, г).

При _   с ростом подачи напор снижается; при _ =  он не зависит от подачи, а при _   напор растет (рис.20, д).

Для осевых машин

(33)

где ^'₂ – угол притекания на выходе из рабочего колеса.

Так как у осевых машин всегда ^'_  , то напор с ростом подачи снижается.