Цилиндр, катающийся в подвижном желобе

В качестве следующего примера выбран катящийся цилиндр в подвижном желобе.

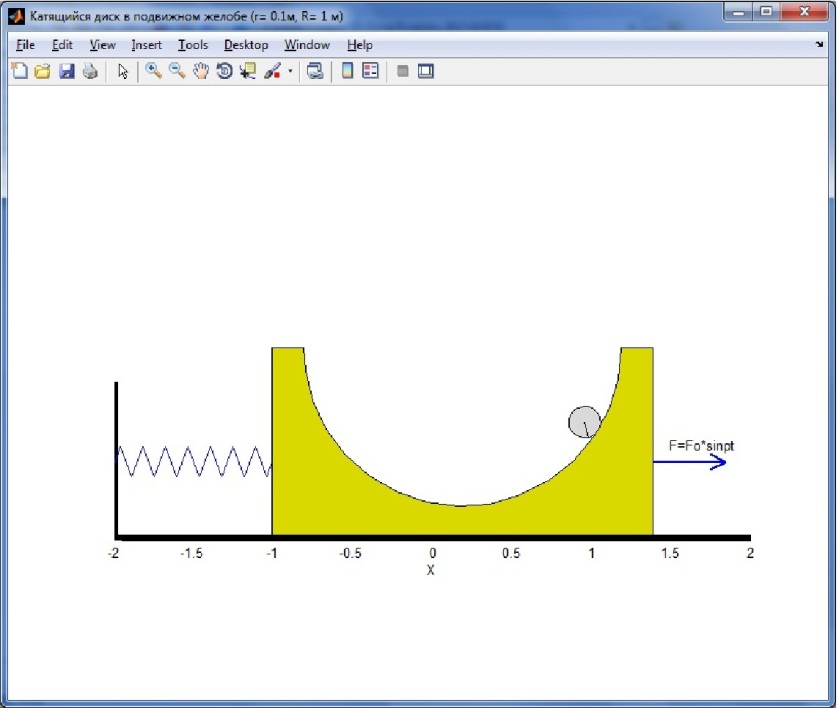
В брусе массы m₁ сделана цилиндрическая выточка радиуса R, в которой катается без скольжения однородный круглый цилиндр массы m₂ и радиуса r. Оси выточки и цилиндра параллельны. Брус двигается по гладкой горизонтальной плоскости под действием горизонтальной силы F=F₀ sin pt, силы упругости F_упр = –cx и силы сопротивления F_сопр =–k . Ось пружины горизонтальна. При x=0 пружина не деформирована.

Уравнения движения Лагранжа 2-го рода имеют вид:

Зададим численные значения параметров и начальных условий:

кг	м	м
Н	с-1	Н/м
Нс/м		м
рад	м/с	с-1

Для рассматриваемой голономной механической системы в качестве обобщенных координат приняты x, φ.

Задание.

Создайте файл dinamika.m и напишите функции dinamika и f аналогично алгоритму уже рассмотренной задачи визуализации динамики диска с маховиком. В функции dinamika необходимо реализовать:

• запрос данных о численных параметрах системы и начальных условиях интегрирования системы;

• интегрирование заданных уравнений движения;

• построение фазовых портретов;

• визуализацию динамики системы.

Запрос данных о численных параметрах системы «цилиндр в подвижном желобе» вынесите в отдельный скрипт аналогично вышерассмотренному скрипту param для диска с маховиком. Не выписывая полностью исходный код функции Param, укажем значения параметров по умолчанию для рассматриваемой системы.

g=9.8; % м/сек

m1=5; % Масса тележки (кг)

m2=1; % Масса цилиндра (кг)

R=1; % Радиус выемки

r=0.1; % Радиус цилиндра

c=10 ; % Жесткость пружины (н/м)

k=3; % Коэфф. сопротивления

Fo=1; % Амплитуда силы (н)

p=0.4; % Циклич. частота (1/сек)

t0=0; % Начальное время интегрирования (сек)

y0=' 0.1 , 1 , 0 , 0 ' ; % Начальные условия (задача Коши) - вектор-столбец из величин x, fi, dx/dt, dfi/dt .

tfin= 5; % Конечное время интегрирования (сек)

step=0.05; % Шаг выдачи результатов интегрирования (сек)

% Параметры пружины :

n_w=7; %10; % Кол-во витков

l_=0.2; 0.3; % Длина одного звена пружины

h_kr=0.5; % Высота точки крепления пружины

% Изображение вектора силы

Foo=0.5; % Длина вектора изображения силы Fo

lstr=Foo/5; % Длина стрелки изображения силы Fo

Ostr=pi/6; % Угол острия стрелки изображения силы Fo

Ниже приводится исходный код функции f0, f1 из файла Kadr. Как и прежде, Kadr предназначен для визуализации системы, вызывается из функции dinamika. F0 и f1 предназначены для полной и частичной перерисовки изображения аналогично вышерассмотренным одноименным функциям в примере «диск с маятником».

function f0(t,x)

global r R p hhh h_kr Foo lstr Ostr h_kola text1 text2 text3 text4 xlm

global h_fig h_J h_vert h_D h_r h_pruj h_F h_txt h_txt2

x1=x(1); % Середина ползуна

% Первоначальное построение

h_fig=figure('Position',[50 50 800 600],...%Положение верхнего угла, ширина, высота окна

'NumberTitle','off','Color',[1 1 1],'Tag','fig',...

'Resize','on','Name',...

['Катящийся диск в подвижном желобе (r= ',num2str(r),'м, R= ',num2str(R),' м)']);

xlm=2;

xlim([-xlm xlm]); % Задание "размера" оси х

set(gca,'Tag','Osi')

set(gca,'ActivePositionProperty','position')

set(gca,'Box','off')

set(gca,'YColor','w')

axis('equal');

text1='F=Fo*sinpt'; % Текст вблизи вектора силы

text2='t= '; text3=num2str(t); text4=' sec';

h_txt2=text(xlm*0.8,xlm*0.9,[text2,text3,text4]);

hold on;

h_plane=0.02; % Высота неподвижной плоскости

h_kola=1; % Высота кола

%Неподвижное основание и кол :

h_osnov=line([-2 -2 2],[h_kola h_plane h_plane],'LineWidth',5,'Color','k');

%Формирование желоба

hhh=1.2*R+h_plane; % Высота ползуна

thp=0:pi/20:pi; % Выемка желоба :

xp=R*cos(thp); % справа (вниз) налево

yp=-R*sin(thp);

% Координаты контура ползуна. Начальный сдвиг желоба на величину x(1)

xp=x1+[xp,-(1.2*R),-(1.2*R),(1.2*R),(1.2*R) ];% Сдвиг желоба на величину x(1)

yp=hhh+[yp,0,-(1.2*R),-(1.2*R),0 ];

h_J=fill(xp,yp,[0.85, 0.85, 0],'Clipping','off',...

'Tag','Jelob'); %Рисование и заливка желоба цветом

ylim([0 2]); % (2) Ось y строится с нуля

%Вектор силы, приложенной к ползуну :

xbeg=x1+1.2*R; % Координаты начала вектора

ybeg=h_kola/2; % Координаты начала вектора

Ugol=0; % Задаем направление

F=Foo*sin(p*t); % Проекция вектора на заданное направление

[xF,yF]=Vector_(xbeg,ybeg,Ugol,F,lstr,Ostr);

h_F=line(xF,yF,'LineWidth',2,'Color',[0, 0, 1]);

h_txt=text(x1+1.2*R+0.1,h_kola/2+0.1,text1); %Координаты начала текста

% в единицах разметки осей

% Параметры пружины :

L=abs(x1-1.2*R+2); % Текущая длина пружины (расст. от кола до левого края ползуна)

x12=[-2,-2+L]; % Координаты x концов пружины

y12=[h_kr,h_kr]; % Координаты y концов пружины

[x_,y_]=Prujina_(x12,y12); % Координаты концов звеньев пружины

h_pruj=line(x_,y_); % Первоначальное построение пружины

% Коррекция свойств осей

set(gca,'Box','off')

set(gca,'ActivePositionProperty','position')

set(gca,'CameraPositionMode','manual')

xlabel('X');

ylabel('Y');

axis('on');

hold on;

%Формирование центральной линии желоба

c1_x=x1;

c1_y=hhh+[0 -R];

h_vert=plot(c1_x,c1_y,'k--','Visible','off'); % Отмена/рисование центр. линии желоба

% Начальное положение диска

tet=x(2);

xc=x1+(R-r)*sin(tet); % Координата x центра диска

yc=hhh-(R-r)*cos(tet); % Координата y центра диска

[xd,yd]=Okr_(xc,yc,r); %Фoрмирование контура диска

% Начальное положение метки диска

psi=tet*(R-r)/r; % Угол поворота диска

xm_c=r*sin(psi); % Проекция радиуса-метки на ось x

ym_c=r*cos(psi); % Проекция радиуса-метки на ось y

xm= xc+xm_c; % Координата x конца метки

ym=yc+ym_c; % Координата y конца метки

h_D=fill(xd,yd,[0.85, 0.85, 0.85]); % Диск

h_r=plot([xc xm],[yc ym], 'k--'); % метка

hold on;

Исходный код вспомогательной функции f1.

function f1(t,x)

global r R Foo lstr Ostr p t_pause k_uskor hhh h_kr h_kola text1 text2 text3 text4 xlm

global h_J h_vert h_D h_r h_pruj h_F h_txt h_txt2

x1=x(1); % Середина ползуна

%Формирование текущего положения желоба

thp=0:pi/20:pi;

xp=R*cos(thp);

yp=-R*sin(thp);

% Координаты контура ползуна (сдвиг желоба на величину x(1) )

xp=x1+[xp,-(1.2*R),-(1.2*R),(1.2*R),(1.2*R) ]; % Сдвиг желоба на величину x(1)

yp=hhh+[yp,0,-(1.2*R),-(1.2*R),0 ];

% Параметры пружины :

L=abs(x1-1.2*R+2); % Текущая длина пружины (расст. от кола до левого края ползуна)

x12=[-2,-2+L]; % Координаты x концов пружины

y12=[h_kr,h_kr]; % Координаты y концов пружины

[x_,y_]=Prujina_(x12,y12); % Координаты концов звеньев пружины

%Вектор силы, приложенной к ползуну :

xbeg=x1+1.2*R; % Координаты начала вектора

ybeg=h_kola/2; % Координаты начала вектора

Ugol=0; % Задаем направление

F=Foo*sin(p*t); % Проекция вектора на заданное направление

[xF,yF]=Vector_(xbeg,ybeg,Ugol,F,lstr,Ostr);

delete(h_txt);

h_txt=text(x1+1.2*R+0.1,h_kola/2+0.1,text1); %Координаты начала текста в

% единицах разметки осей

if round(t)-t==0 % Показ времени

delete(h_txt2);

text3=num2str(t);

h_txt2=text(xlm*0.8,xlm*0.9,[text2,text3,text4],...

'BackgroundColor',[.7 .9 .7],'LineWidth',2 ); %Координаты показа t=

end;

%Формирование центральной линии желоба

c1_x=x1;

c1_y=hhh+[0 -R];

%Искусственное расширение графика (по высоте) для исключения эффекта

%движения неподвижного основания. Иначе матлаб динамически подгоняет

% размеры под реальные (можно отключить опцию Resize = on ).

set(h_vert,'EraseMode','none');

% Текущее положение диска

tet=x(2);

xc=x1+(R-r)*sin(tet); % Координата x центра диска

yc=hhh-(R-r)*cos(tet); % Координата y центра диска

[xd,yd]=Okr_(xc,yc,r); %Фoрмирование контура диска

% Текущее положение метки на диске

psi=tet*(R-r)/r; % Угол поворота диска

xm_c=r*sin(psi); % Проекция радиуса-метки на ось x

ym_c=r*cos(psi); % Проекция радиуса-метки на ось y

xm= xc+xm_c; % Координата x конца метки

ym=yc+ym_c; % Координата y конца метки

pause(t_pause/k_uskor); % Ускорение/замедление показа

set(h_J,'XData',xp);

set(h_J,'YData',yp);

set(h_vert,'XData',c1_x);

set(h_vert,'YData',c1_y);

set(h_D,'XData',xd);

set(h_D,'YData',yd);

set(h_r,'XData',[xc xm]);

set(h_r,'YData',[yc ym]);

set(h_pruj,'XData',x_);

set(h_pruj,'YData',y_);

set(h_F,'XData',xF);

set(h_F,'YData',yF);

Задания.

1. Отладить и запустить программу визуализации динамики цилиндра, катающегося в подвижном желобе.

2. Для системы «цилиндр, катающийся в подвижном желобе» написать программу:

1. нахождения положения равновесия,

2. линеаризации дифференциальных уравнений в окрестности найденного положения равновесия,

3. составления характеристического уравнения

4. нахождения его корней.

При написании программы можно опираться на алгоритм, реализованный в разделе «Диск с маятником. Уравнения равновесия системы».

3. Какие динамические эффекты можно наблюдать в рассматриваемой системе? Попробуйте воспроизвести их.