Динамические эффекты на примере диска с маятником
В данном разделе для уже рассмотренной задачи рассматривается подбор параметров системы, позволяющих увидеть такие явления, как динамическое гашение вынужденных колебаний, виброустойчивость и резонанс.
Динамическое гашение
Рассмотрим систему диск с маятником со следующими параметрами:
g=9.8; % м/сек
m1=1; % Масса диска (кг)
m2=0.02; %0.02; % Масса груза (кг)
r=0.2; % Радиус диска
l=0.2; % Длина стержня (м)
c=1.95 ; % Жесткость спиральной пружины O (Нм)
c2=1 % Жесткость спиральной пружины A (Нм)
fi_z=0;
k1=0.05 % Коэфф. сил сопр. на оси O
k2=0 % Коэфф. сил сопр. на оси A
e=r/sqrt(3);
M0= 0.2; % Амплитуда момента, приложенного к диску
p0=7;
% Парциальные частоты : om1 = 10.1745: om2 = 17.2916
gam=pi/2; % Начальная фаза
t0=0; % Начальное время интегрирования (сек)
y0=' 2*pi/3 , 0 , 0. , 0 ' ; % Начальные условия - положение равновесия
tfin=20; 10; % Конечное время интегрирования (сек)
step=0.025; 0.1; % Шаг выдачи результатов интегрирования (сек)
% Параметры изображения спиральной пружины пружины :
Wit=2; %10; % Кол-во витков в исходном состоянии
r1=e/20; % Полярная координата внутреннего конца пружины
r2=e/3; % Полярная координата внешнего конца пружины
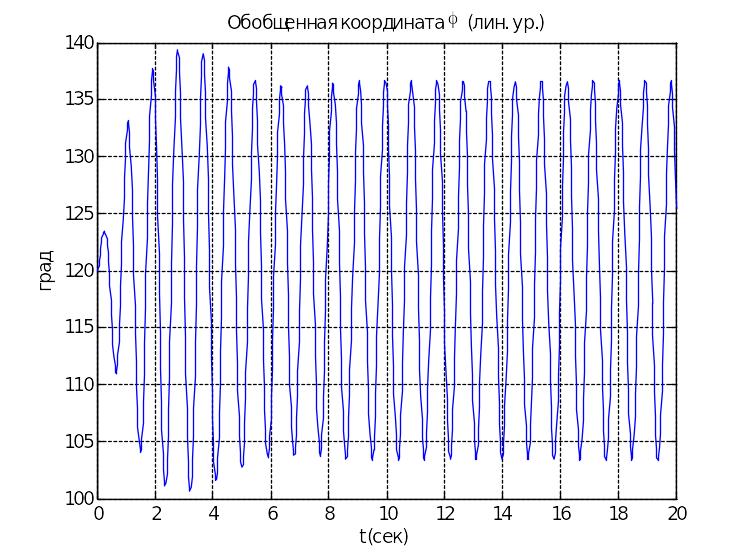
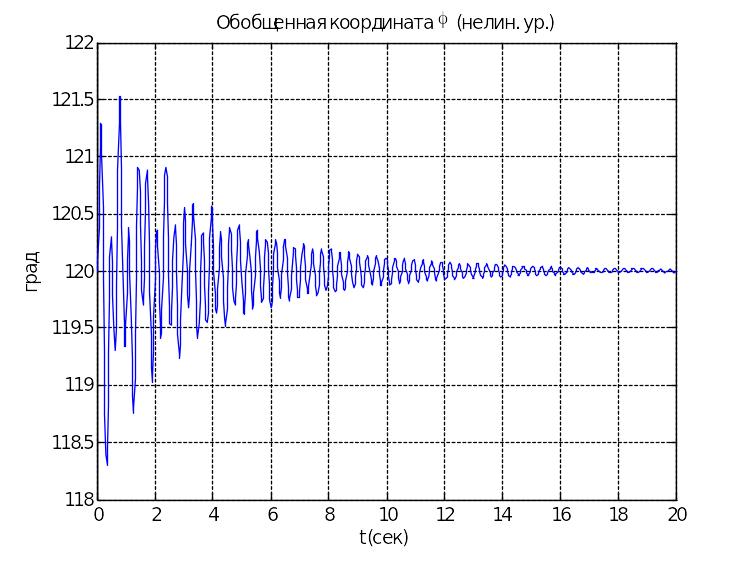
При интегрировании системы с вышеуказанными параметрами получим следующие графики:
Линейная система |
Нелинейная система |
|
|
|
|
|
|
При
наблюдается гашение колебаний диска,
что выражается в уменьшении амплитуды
угла φ.
Линейная система |
Нелинейная система |
|
|
|
|
Виброустойчивость
Рассмотрим систему диск с маятником со следующими параметрами системы
g=9.8; % м/сек
m1=1; % Масса диска (кг)
m2=0.002 %0.2; % Масса груза (кг)
r=0.2; % Радиус диска
l=0.1; 0.15; % Длина стержня (м)
c=10000; %T=0.0297сек % 20000; T=0.0210сек % Жесткость спиральной пружины (Нм)
e=r/sqrt(3)
fi_z=pi/6-(m1/2+2*m2)*e*g/c %закрутка пруж.(в пол. равн. OA - горизонтально)
M0=0; 0.02; % Амплитуда момента, приложенного к диску
p=0.; % Переменная циклическая частота момента, приложенного к диску Omega= p*t +p0
p0= 4.6887; % циклическая частота момента, приложенного к диску gam=pi/2; % Начальная фаза
t0=0; % Начальное время интегрирования (сек)
y0=' pi/6+0.03 , pi , 0 , 5 ' ; % Начальные условия для виброуст.
%Добавка к pi/6 - амплитуда колебаний диска (определяет gam на диаграмме Матье)
tfin=5; 10; % Конечное время интегрирования (сек)
step= 0.001; 0.1; % Шаг выдачи результатов интегрирования (сек)
% Параметры спиральной пружины пружины :
Wit=2; %10; % Кол-во витков в исходном состоянии
r1=e/20; % Полярная координата внутреннего конца пружины
r2=e/3; % Полярная координата внешнего конца пружины
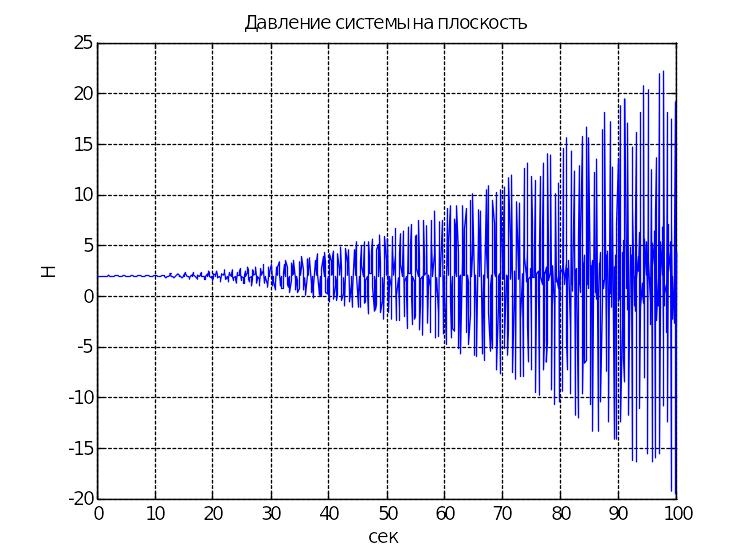
При указанных численных параметрах системы наблюдается виброустойчивость. В нашем примере амплитуда колебаний в окрестности верхнего положения составляет порядка 12 градусов. Для поддержания заданного режима диск колеблется в окрестности угла φ=30 градусов с амплитудой 1,7 градусов и частотой 85 Гц (см. график).
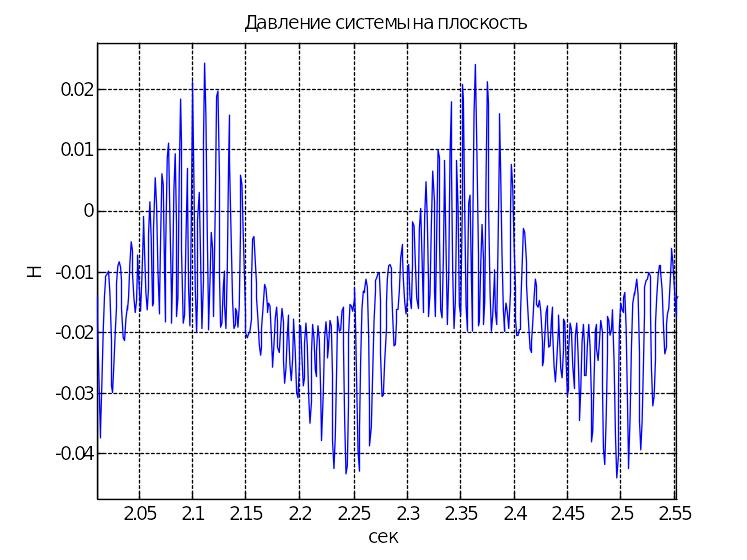
Резонанс
При следующих параметрах системы наблюдается резонанс.
g=9.8; % м/сек
m1=1; % Масса диска (кг)
m2=0.2; % Масса груза (кг)
r=0.2; % Радиус диска
l=0.2; % Длина стержня (м)
c=1.95 ; % Жесткость спиральной пружины (Нм)
fi_z=0;
e=r/sqrt(3);
M0= 0.02; % Амплитуда момента, приложенного к диску
p0= 4.6887% циклическая частота момента
gam=pi/2; % Начальная фаза
t0=0; % Начальное время интегрирования (сек)
y0=' 0.52094380244489 , 0 , 0 , 0 ' ; % Начальные условия - положение равновесия
tfin= 100; % Конечное время интегрирования (сек)
step= 0.1; 0.05; % Шаг выдачи результатов интегрирования (сек)
% Параметры спиральной пружины пружины :
Wit=2; %10; % Кол-во витков в исходном состоянии
r1=e/20; % Полярная координата внутреннего конца пружины
r2=e/3; % Полярная координата внешнего конца пружины
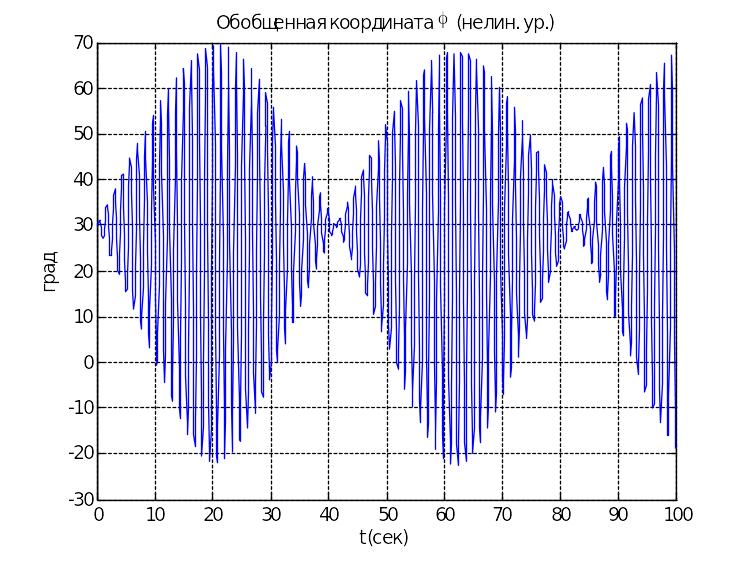
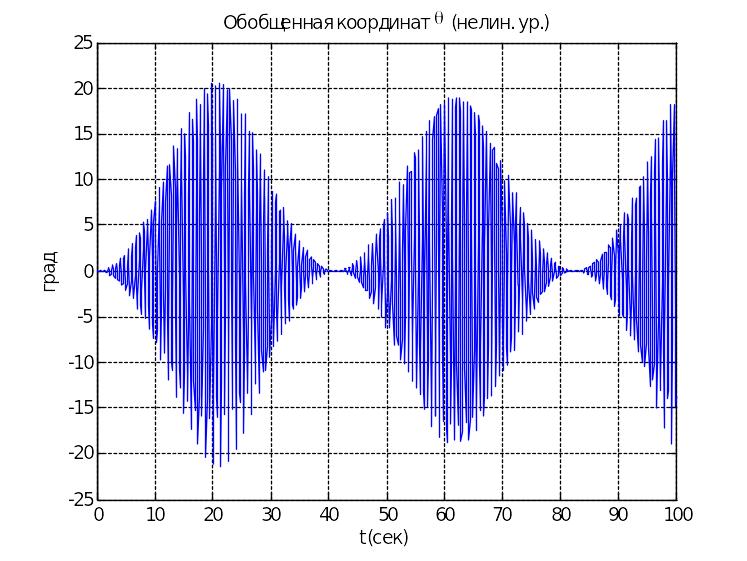
При интегрировании системы с указанными параметрами получаем следующие графики, из которых видно, что на интервале времени от 0 до 10 секунд решения линейной и нелинейной систем практически совпадают. В дальнейшем использование линейных уравнений приводит к неправильным результатам, как видно из сравнения графиков. В нелинейной системе наблюдается периодическое гашение колебаний с частотой 0,025 Гц, т.е.наблюдаются так называемые субгармонические колебания.
Линейная система |
Нелинейная система |
|
|
|
|
|
|
