Спираль

Входные параметры:

r1,r2,fi1,fi2 – полярные координаты концов спиральной пружины

Wit – количество витков

Выходные параметры:

x, y – координаты точек, составляющих спираль.

function [x,y]=Spiral_(r1,r2,fi1,fi2,Wit)

fi=0 : pi/30 : fi2-fi1 + 2*pi*Wit;

r=r1+(r2-r1)/(fi2-fi1+2*pi*Wit)*fi;

x=r.*cos(fi);

y=r.*sin(fi);

Пример вызова:

Wit=3

r1=0.05;

r2=0.3;

fi1=0

fi2=0.5

[x,y]=Spiral_(r1,r2,fi1,fi2,Wit);

h_plot=plot(x,y)

xlm=0.5;

xlim([-xlm xlm]); % Задание "размера" оси х

axis equal

tic

N=200;

step=0.05

for i=1:N

fi2=fi2+step;

[x,y]=Spiral_(r1,r2,fi1,fi2,Wit);

% Перепостроение графиков

pause(0.01);

set(h_plot,'XData',x);

set(h_plot,'YData',y);

end;

toc

Результат вызова:

Пружина

Входные параметры:

координаты x и y начала и конца пружины.

Выходные параметры

x,y координаты изломов пружины.

Число n_w изломов пружины и длину l_ участка пружины, соединяющего две вершины пружины, определим как глобальные переменные. Для построения изображения в вызывающей программе после выполнения программы необходимо вызвать команду line(x,y) или plot(x,y).

function [x,y]=Prujina_(x12,y12)

global n_w l_

% Вычисление координат изломов пружины в исходном горизонтальном положении

% с началом в точке (0,0) :

x1=x12(1); y1=y12(1);

x2=x12(2); y2=y12(2);

L=sqrt((x1-x2)^2+(y1-y2)^2); % Текущая длина пружины

Lmax=2*n_w*l_;

if Lmax- L >= 0 % Проверка условия существования пружины с такими параметрами

del=L/n_w/2; % Половина длины шага пружины (половина расстояния между соседними зубцами)

r_=sqrt(l_^2-del^2)/2; %

x0=[0 del/2 : del : L-del/2 L]; % Координаты x изломов пружины

y_v=r_*ones(1,n_w); % Координаты y верхних изломов пружины

y_n=-r_*ones(1,n_w); % Координаты y нижних изломов пружины

y_vn=[y_v;y_n]; % Слияние координат y в матрицу

sz=size(y_vn);

y__= reshape(y_vn,1,sz(1)*sz(2)); % Преробразование матрицы 2хn в матрицу 1х2n, т.е. вектор.

y0=[0 y__ 0]; % Добавление крайних точек

else

disp('Увеличь максимальную длину Lmax пружины!')

beep

end

% Вычисление координат изломов пружины в повернутом положении

% с началом в точке (0,0) :

stet=(y2-y1)/L; % Синус и косинус угла поворота пружины

ctet=(x2-x1)/L;

x=x0*ctet-y0*stet+x1;

y=x0*stet+y0*ctet+y1;

Пример вызова:

global n_w l_

figure(1)

n_w=10 % Число витков

l_=1 % Длина звена

x12=[0 5] % Координаты x концов пружины

y12=[0 5] % Координаты y концов пружины

[x,y]=Prujina(x12,y12); % Вычисление координат изломов пружины

hold off

plot(x,y); % Построение пружины

% Координаты начала текста :

xt=x12(1)+(x12(2)-x12(1))/5;

yt=y12(1)+(y12(2)-y12(1))/2;

ht=text(xt,yt,'Press ','FontSize',18)

pause(0.5)

ht=text(xt,yt,' Enter !','FontSize',18)

pause

x12=x12+1;

y12=y12-1;

xbeg=x12(1);

xend=x12(2);

ybeg=y12(1);

yend=y12(2);

[x,y]=Prujina(x12,y12); %Координаты изломов пружины

plot(x,y); % Построение пружины

% Добавление маркеров на концах пружины :

h_beg=line(xbeg,ybeg, 'Marker','o','MarkerSize',8,'LineWidth',1,'Color','k');

h_end=line(xend,yend, 'Marker','.','MarkerSize',60,'Color','b');

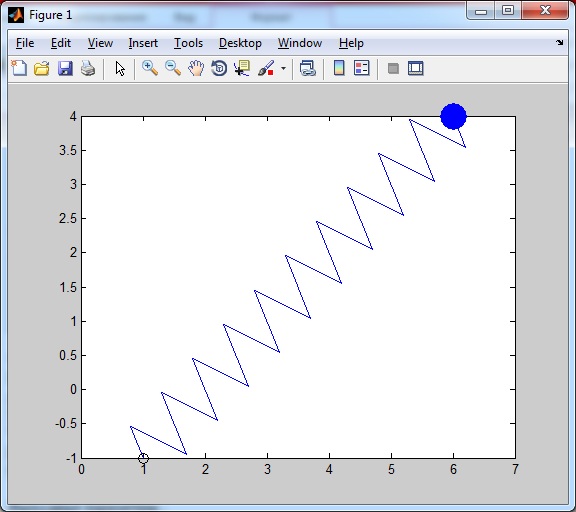
Результат:

После нажатия кнопки Enter:

Вектор

Входные параметры:

xbeg,ybeg - координаты начала вектора

Ugol (рад) - угол между осью x и направлением вектора

V=2 - проекция вектора на заданное направление

lstr - длина стрелки на конце вектора

Ostr - угол полураствора стрелки

Выходные параметры :

x,y - координаты элементов вектора

function [x,y]=Vector_(xbeg,ybeg,Ugol,V,lstr,Ostr)

% Сначала горизонтальный вектор

x_=[xbeg, xbeg+ V ]; % Горизонтальный отрезок

y_=[ybeg , ybeg ]; % Горизонтальный отрезок

sgnV=sign(V);

xs=[x_(2)-sign(V)*lstr, x_(2),x_(2)-sign(V)*lstr]; % Стрелка на конце

h=sin(Ostr)*lstr;

ys=[ybeg+ h , ybeg, ybeg- h]; % Стрелка на конце

x__=[x_, xs]; % объединение отрезка и стрелки

y__=[y_, ys]; % объединение отрезка и стрелки

% Поворот горизонтального вектора вокруг начала на угол Ugol

sU=sin(Ugol); % Синус и косинус угла поворота

cU=cos(Ugol);

x=x__*cU-y__*sU;

y=x__*sU+y__*cU;

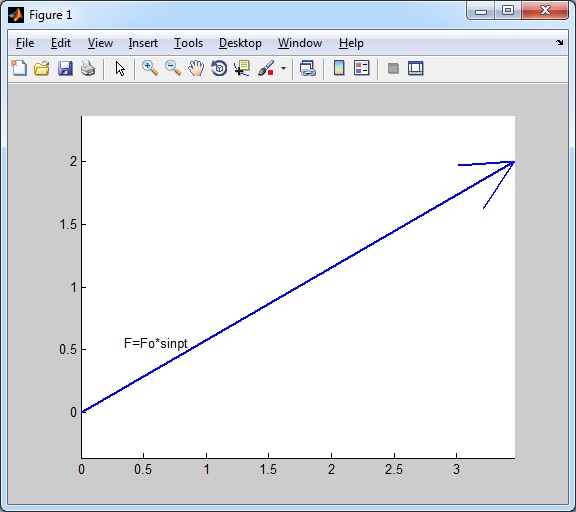
Пример вызова:

xbeg=0

ybeg=0

Ugol=pi/6 % Направление вектора

V=4; -2 % Проекция вектора на заданное направление

Lstr=0.4 % Длина стрелки

Ostr=pi/6 % Угол раствора стрелки

[x,y]=Vector_(xbeg,ybeg,Ugol,V,Lstr,Ostr);

h_F=line(x,y,'LineWidth',2,'Color',[0, 0, 1]);

axis equal

text1='F=Fo*sinpt';

xlm=xlim; % Границы оси x

ylm=ylim; % Границы оси y

xtxt=xbeg+(xlm(2)-xlm(1))/10; %Координаты начала текста

ytxt=ybeg+(ylm(2)-ylm(1))/5; %Координаты начала текста

h_txt=text(xtxt,ytxt,text1); % в единицах разметки осей

Результат: