1.2. Условия макроскопического проявления и направление

процессов переноса

Как уже отмечалось в предыдущем разделе, при решении инженерных задач используется в основном макроскопический уровень описания систем. Поэтому нас интересуют макроскопические условия проявления процессов переноса. Если система находится в состоянии равновесия, то макроскопических проявлений переноса субстанции не наблюдается. Несмотря на тепловое движение молекул, каждая из которых переносит массу, импульс и энергию, макроскопические потоки субстанции при этом отсутствуют вследствие равновероятности переноса в каждом направлении. Конвективный и турбулентный механизмы переноса в условиях равновесия вообще отсутствуют.

Равновесие в однофазной системе устанавливается при равенстве значений в каждой точке пространства макроскопических величин, характеризующих свойства системы: скорости - (x,y,z,t) = const; температуры - T(x,y,z,t) = const; химических потенциалов компонентов - _i(x,y,z,t) = const.

Последняя величина характеризует изменение энергии системы при изменении количества частиц сорта i в ней. Химический потенциал компонента может быть выражен через стандартную часть и произведение коэффициента активности на мольную долю соответствующего компонента :

. (1.9)

Для системы, состоящей из двух фаз, условием равновесия является равенство приведенных выше величин в каждой из фаз:

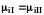, , . (1.10)

Можно выделить отдельно условия гидромеханического, теплового и концентрационного равновесия:

гидромеханическое равновесие : =const; ;

тепловое (термическое) равновесие : Т=const; ;

концентрационное равновесие : =const, ,

здесь - дифференциальный оператор (см. приложение П.1.3).

Условием проявления процессов переноса и возникновения макроскопических потоков массы, импульса и энергии является неравновесность системы. Направленность процессов переноса определяется самопроизвольным стремлением системы к состоянию равновесия, т.е. процессы переноса приводят к выравниванию скорости, температуры и химических потенциалов компонентов системы. Неоднородности указанных величин являются необходимыми условиями протекания процессов переноса, их называют движущими силами.

Для того чтобы осуществить процесс, необходимо вывести систему из состояния равновесия, т.е. оказать воздействие извне. Это возможно за счет подвода массы или энергии к системе либо действия внешних сил. Например, отстаивание происходит в поле сил тяжести, а центрифугирование - в поле центробежных сил, выпаривание - при подводе тепла, абсорбция - при введении в систему поглотителя.

1.3. Уравнения переноса

В данном разделе рассматриваются локальные уравнения переноса субстанции (массы, импульса и энергии), т.е. уравнения, справедливые для каждой отдельной точки пространства. Рассмотрение ведется на макроскопическом уровне - все используемые величины являются макроскопическими. Задача заключается в получении математического выражения для потока субстанции (количество субстанции, переносимое за единицу времени, через единицу поверхности) за счет различных механизмов переноса.