4.4.2. Интегральная форма уравнений

Осреднив локальные уравнения межфазного переноса субстанций по участку поверхности, можно получить интегральную форму уравнений:

, (4.109)

, (4.110)

. (4.111)

Рис. 4.4. Профиль температуры для процесса теплопередачи через стенку толщиной  .

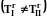Как и для уравнений (4.15)-(4.17), в общем случае при одновременном изменении кинетического коэффициента и движущей силы по межфазной поверхности такая запись является условной, так как невозможно разделить осреднение кинетического коэффициента и движущей силы. Аналогично (4.18)-(4.21) можно независимым образом осреднить одну из величин, но тогда значение второй будет зависеть от характера изменения первой.

Более того, использование уравнений (4.109)-(4.111) усложняется по сравнению с (4.15)-(4.17) возможностью различного относительного движения фаз. Выделяют следующие схемы (рис. 4.5.):

а) прямоток или параллельный ток (движение фаз в одном направлении);

б) противоток (движение фаз в противоположных направлениях);

в) перекрестный ток (движение фаз во взаимно перпендикулярных направлениях);

г) смешанный ток (движение одной из фаз в одном направлении, а другой как в одном, так и в противоположном направлениях).

Рис. 4.5. Схемы относительного движения фаз: а - прямоток, б - противоток, в - перекрестный ток, г - смешанный ток

Если для вариантов а и б при осреднении по F достаточно интегрирования по одной координате х, то для вариантов в и г необходимо интегрировать по координатам х и z. Кроме того, найденный по соотношению, аналогичному (4.18), осредненный кинетический коэффициент межфазного переноса не будет тождествен полученному по (4.97)-(4.99) с использованием предварительно осредненных по (4.18) коэффициентов массо-, тепло- или импульсоотдачи. Строгий подход предполагает непосредственное интегрирование в уравнениях (4.109)-(4.111).

Рассмотрим, например, стационарный процесс теплопередачи при прямоточном движении фаз вдоль плоской поверхности шириной Z в направлении оси Х при толщине слоев Y_I и Y_II, соответственно. Термическим сопротивлением межфазной поверхности можно пренебречь. Используем диффузионную модель структуры потока в каждой из фаз с коэффициентами обратного перемешивания D_LI и D_LII, дополнив соответствующие уравнения источниками (стоками) тепла за счет теплопередачи.

Математическая модель будет иметь вид

, (4.112)

, (4.113)

, (4.114)

, (4.115)

, (4.116)

, (4.117)

, ;

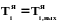, , (4.118)

В данном случае предполагается известной зависимость коэффициентов теплоотдачи как от расстояния от начала поверхности (через толщину пограничного слоя), так и от температур ядра фазы и ее границы (через зависимость от теплофизических свойств). Решение системы уравнений (4.112)-(4.117) с граничными условиями (4.118), по-видимому, с помощью численных методов позволяет получить явную зависимость от x величин Т^я_I, Т^я_II, Т^г, K_т, _I, _II. Тогда можно воспользоваться уравнением (4.119) и найти количество передаваемого тепла за единицу времени на участке длиной L:

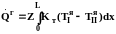. (4.119)

На практике при расчете промышленных аппаратов, как правило, пренебрегают изменением кинетических коэффициентов межфазного переноса, используют их значения, найденные через осредненные коэффициенты массо-, тепло-импульсоотдачи, а среднюю движущую силу для прямоточного и противоточного движения считают как среднелогарифмическую (соотношение типа (4.31) будет выполняться и для межфазного переноса при постоянных теплофизических свойствах фаз и модели идеального вытеснения). Для перекрестного и смешанного тока вводится поправочный коэффициент, уменьшающий величину средней движущей силы. Однако, прежде чем воспользоваться этими упрощениями, следует оценить ошибку, которую они могут дать в условиях рассматриваемой задачи.

- 110 -