Проведение эксперимента и его обработка. Изучение структуры потока будет заключаться в измерении полей скоростей на модели. Обеспечив подобие с оригиналом, результаты могут быть представлены в виде

, . (3.48)

Это позволяет предсказать поля скоростей в оригинале по измерениям скоростей на модели:

, . (3.49)

Для обеспечения возможности оптимизации объекта-оригинала проводятся несколько серий экспериментов при различных Rе^m, L^m/d₀^m, L^m/d^m . Это позволяет представить результаты совокупности измерений как частное решение системы уравнений (3.34)-(3.36) с соответствую-щими условиями однозначности:

, (3.50)

где выделены различные виды обобщенных переменных: независимые (две первые), зависимые (три последующие), постоянные (четыре последние).В дальнейшем определяющие критерии подобия (составленные из величин, входящих в условия однозначности) будем использовать, как правило, без индексов в отличие от локальных. Или в явном виде вместо (3.50)

, . (3.51)

Соотношения (3.51) являются экспериментально найденным частным решением уравнений (3.34)-(3.36), т.е. критериальным аналогом (3.37). Они справедливы как для модели, так и для оригинала при соблюдении подобия условий однозначности в исследованном диапазоне изменения параметров .

Использование результатов. Основная цель изучения гидродинамической структуры потоков состоит в учете ее влияния на тепло- и массообменные процессы. Полученные соотношения (3.51) являются решением уравнений Навье-Стокса и неразрывности. Это позволяет заменить данные дифференци-альные уравнения в исчерпывающем описании найденными соотноше-ниями, определяющими поле скоростей. В зависимости от поставленной задачи соотношения (3.51) решаются совместно с уравнением нестационарной конвективной теплопроводности или диффузии. Это существенно упрощает задачу.

Кроме того, измерение на модели не только поля скоростей, но и поля давления позволяет получить критериальные уравнения, которые можно использовать для расчета гидравлического сопротивления аппарата (потери давления р):

(3.52)

Совокупность этих результатов позволяет оптимизировать форму и размеры оригинала, а также условия проведения в нем процесса.

3.5.4. Сопряженное физическое и математическое моделирование структуры потоков

Для рассмотрения основных этапов моделирования структуры потока данным методом воспользуемся примером проточного аппарата.

Выделение характерных зон аппарата. Анализ поведения турбулентного потока в аппарате (см. рис. 3.2) позволяет выделить 8 характерных зон [6]: 1, 7 - застойные зоны; 2, 6 - зоны смешения; 3 - пограничный слой; 4, 5, 8 - ядро потока. Разграничение характерных зон носит достаточно условный и субъективный характер. На этом этапе возможны различные варианты.

Экспериментальное изучение отдельных зон на физических моделях. Экспериментальное определение поля скоростей в каждой зоне проводится на физической модели, причем не обязательно модели всего аппарата. Так, например, проточный аппарат заменялся тремя моделями: уступа (а), трубы (б), области сужения потока (в) (рис. 3.5) [6]

Рис. 3.5. Схема физических моделей проточного аппарата: а - уступ, б - труба, в - область сужения потока.

Составление математических моделей отдельных зон. Цель данного этапа - определение базисных функций _i (3.5). В рассматри­ваемом примере нас интересуют поля скоростей, следовательно, необходимо определить W_х, W_r в каждой из характерных зон. Вид базисной функции отдельной зоны неоднозначен. Экспериментальные данные могут аппроксимироваться различными зависимостями. При выборе вида функции необходимо учитывать соблюдение граничных условий и сопряжения на границах зон, а также предусматривать инвариантность вида функции к масштабу аппарата. Для выполнения последнего целесообразно записывать базисные функции в обобщенных переменных, используя теорию подобия. Так, например, в [6] предложены следующие базисные функции:

для зоны 1:

,

,

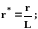
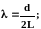
для зоны 2:

,

,

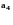где a_j - параметры, отражающие взаимодействие между зонами; , d₀, L, d - совокупность режимных и геометрических параметров. В предложенном виде функции не содержат в явном виде физические свойства среды (, ), но в неявном виде они учитываются в параметрах а_j. Всего базисные функции W*_хi для 8 характерных зон содержат 11 параметров а_j. Базисные функции W*_ri находятся из уравнения неразрывности (3.36). Для поля скоростей, определенного на физической модели, параметры а_j, найденные аппроксимацией экспериментальных данных, представляют собой числа. При изменении масштаба, геометрии аппарата или свойств движущейся среды предполагается сохранение вида базисных функций и изменение лишь значений параметров а_j.

Синтез и идентификация модели аппарата. Математической моделью объекта - оригинала является совокупность моделей характерных зон, представляющих собой базисные функции с неизвестными параметрами а_j. Целью данного этапа является отыскание последних. Эта задача может решаться на основе двух подходов: проведение экспериментального исследования поля скоростей объекта - оригинала (промышленного аппарата) или удовлетворение математической модели системе дифференциальных уравнений типа (3.34)-(3.36) с условиями однозначности для промышленного аппарата.

Предпочтение отдается второму подходу, так как первый не позволяет решать задачу проектирования и оптимизации. Если бы число неизвестных параметров а_j соответствовало числу уравнений в исчерпывающем описании, то они могли бы быть найдены путем интегрирования системы дифференциальных уравнений по всему объему аппарата с использованием в них в качестве W_х, W_r базисных функций с последующим решением системы алгебраических уравнений относительно неизвестных а_j. Однако в данном случае, как и в большинстве других, число параметров значительно превышает число уравнений (параметров 11, а уравнений 3). В этом случае для отыскания параметров применяется вариационный метод. Для его реализации необходимо на основе исчерпывающего описания составить функционал, минимизация которого позволит найти искомые параметры.

Авторами метода сопряженного физического и математического моделирования предложено использовать в качестве такого функционала локальный потенциал Гленсдорфа-Пригожина, являющийся критерием стационарного состояния системы [6].

Проверка адекватности модели. Адекватность модели устанавливается по степени ее соответствия исчерпывающему описанию, о чем можно судить по величине локального потенциала Е_л. Точное решение, полностью соответствующее исчерпывающему описанию, неизвестно. Для физической модели за точное решение с погрешностью эксперимента можно принять базисные функции с параметрами а_j^mэ, найденными аппроксимацией экспериментальных данных. Подставив базисные функции с данными значениями параметров в выражение для локального потенциала, можно определить его значение для физической модели Е_л^mэ. С другой стороны параметры для физической модели можно найти из решения системы уравнений (3.61) а_j^mр и соответственно получить E_л^mр. Найдем максимальную погрешность поля скоростей

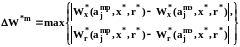(3.62)

и соответствующее расхождение значений локального потенциала

. (3.63)

Произвольно меняя значения параметров а_j^m в окрестности а_j^mэ и исследуя влияние E_л^m на W*^m, можно установить между ними определенную зависимость W*^m = f(E_л^m). Полагая, что данная зависимость сохранится и для объекта-оригинала в силу инвари­антности исчерпывающего описания, можно использовать ее для оценки точности получаемого решения:

, . (3.64)

Если при изменении масштаба, геометрии оригинала (аппарата) или свойств движущейся в нем среды, отличие локального потенциала Е_л^0р от Е_л^mэ выйдет из области, соответствующей допустимым по точности решениям W*⁰, то потребуется коррекция модели. Для этого следует изменить вид базисных функций. С целью более удачного выбора базисных функций возможно проведение дополнительных экспериментальных исследований с новыми условиями однозначности.

Использование модели для проектирования и оптимизации промышленного аппарата. Математическая модель структуры потока в аппарате, представляющая совокупность базисных функций поля скоростей во всех характерных зонах аппарата, может использоваться для описания тепло- и массообменных процессов совместно с уравнениями сохранения массы и энергии. Преимущество рассматриваемого метода моделирования при проектировании промышленных аппаратов заключается в том, что в отличие от математического моделирования нет необходимости идентифицировать модель на гидродинамических стендах промышленного масштаба, а в сравнении с физическим моделированием не накладывается требование подобия процесса для аппарата в целом. Для сохранения структуры базисных функций по сути дела достаточно подобия соответствующих характерных зон. К тому же не требуется проведение серии экспериментальных исследований с целью определения взаимного влияния критериев подобия при изменении условий однозначности. Влияние условий однозначности в методе сопряженного физического и математического моделирования учитывается при составлении базисных функций и подстройке параметров а_j, обеспечивающих минимум локального потенциала Е_л, т.е. максимального удовлетворения исчерпывающему описанию. Это позволяет в полной мере исследовать влияние конструктивных и режимных изменений на протекание процесса в проектируемом аппарате и обеспечить выбор оптимального варианта.

в в аппаратах?