
- •Глава 1. Механизмы и уравнения переноса субстанций
- •1.1. Механизмы переноса
- •1.1.1. Молекулярный механизм
- •1.1.2. Конвективный механизм
- •1.1.3. Турбулентный механизм
- •1.2. Условия макроскопического проявления и направление
- •1.3. Уравнения переноса
- •1.3.1. Перенос массы Конвективный механизм. Поток массы в лабораторной системе отсчета за счет конвективного механизма для любой точки системы может быть связан с конвективной скоростью:
- •Зачастую удобнее использовать поток вещества, а не массы:
- •1.3.2. Перенос энергии
- •1.3.3. Перенос импульса
- •Турбулентный перенос. Перенос импульса за счет турбулентного механизма может рассматриваться по аналогии с молекулярным:
- •Глава 2. Законы сохранения
- •2.1. Закон сохранения массы
- •2.1.1. Интегральная форма закона сохранения массы
- •2.1.2. Локальная форма закона сохранения массы
- •2.2. Закон сохранения энергии
- •2.2.1. Интегральная форма закона сохранения энергии
- •2.2.2. Локальная форма закона сохранения энергии
- •2.3. Закон сохранения импульса
- •2.3.1. Интегральная форма закона сохранения импульса
- •2.3.2. Локальная форма закона сохранения импульса
- •2.4. Исчерпывающее описание процессов переноса
- •2.4.1. Условия однозначности
- •2.4.2. Поля скорости, давления, температуры и концентраций,
- •2.4.3. Аналогия процессов переноса
- •Глава 3. Моделирование
- •3.1. Математическое моделирование
- •3.2. Физическое моделирование
- •3.2.1. Теория подобия
- •3.2.2. Основные этапы физического моделирования
- •3.3. Проблема масштабного перехода при проектировании промышленных аппаратов
- •3.4. Сопряженное физическое и математическое моделирование
- •3.5. Моделирование гидродинамической структуры потоков в аппаратах
- •3.5.1. Структура потоков и ее характеристики
- •3.5.2. Математическое моделирование структуры потоков
- •3.5.3. Физическое моделирование структуры потоков
- •Получение критериев подобия. Для получения критериев подобия воспользуемся алгоритмом, изложенным в разд. 3.2.1. Поделим все члены уравнения (3.34) на первый и отбросим символы дифференцирования:
- •Проведение эксперимента и его обработка. Изучение структуры потока будет заключаться в измерении полей скоростей на модели. Обеспечив подобие с оригиналом, результаты могут быть представлены в виде
- •3.5.4. Сопряженное физическое и математическое моделирование структуры потоков
- •Глава 4. Межфазный перенос субстанций
- •4.1. Уравнения массо-, тепло- и импульсоотдачи
- •4.1.1. Локальная форма уравнений
- •4.1.2. Интегральная форма уравнений
- •4.1.3. Влияние структуры потока в аппарате на движущую силу процесса
- •4.2. Нахождение коэффициентов массо-, тепло- и импульсоотдачи, подобие соответствующих процессов
- •4.3. Аналогия процессов массо-, тепло- и импульсоотдачи
- •4.4 Уравнения массо-, тепло- и импульсопередачи
- •4.4.1. Локальная форма уравнений
- •4.4.2. Интегральная форма уравнений
3.5.3. Физическое моделирование структуры потоков
Рассмотрим основные этапы физического моделирования структуры потоков на примере горизонтального цилиндрического проточного аппарата (рис. 3.2) в стационарных условиях.
Сокращение исчерпывающего описания для объекта-оригинала. Зачастую условия проведения процесса в конкретном аппарате позволяют исключить некоторые члены и даже уравнения исчерпывающего описания. Так как моделируемый объект представляет цилиндрический аппарат, то удобнее его описывать в цилиндрических координатах х, r, . При горизонтальном расположении аппарата и вынужденном движении среды влиянием сил тяжести можно пренебречь. Это позволяет сделать еще одно допущение - осесимметричность движения, т.е. исключить зависимость от угла . Если к тому же рассматривать стационарный случай ламинарного течения при , = const, то с учетом принятых допущений уравнения Навье - Стокса примут вид (см. приложение П.2.2):
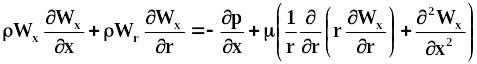 , (3.34)
, (3.34)
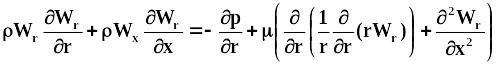 . (3.35)
. (3.35)
Система уравнений дополняется уравнением неразрывности :
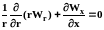 . (3.36)
. (3.36)
Таким
образом, частичное упрощение исчерпывающего
описания позволило трехмерную задачу
трансформировать в двухмерную (одним
уравнением и одной переменной стало
меньше, так как
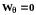 ),
сократилось и число членов в уравнениях
Wx/t
= Wr/t
= 0, gr
= gx
= 0. Система
уравнений (3.34)-(3.36) должна быть дополнена
условиями однозначности. Форма и размер
аппарата задаются диаметрами d0,
d и длиной
L; физические
свойства среды - плотностью
и динамическим коэффициентом молекулярной
вязкости ,
начальные условия отсутствуют, поскольку
рассматривается стационарный случай.
Граничные условия задаются значениями
),
сократилось и число членов в уравнениях
Wx/t
= Wr/t
= 0, gr
= gx
= 0. Система
уравнений (3.34)-(3.36) должна быть дополнена
условиями однозначности. Форма и размер
аппарата задаются диаметрами d0,
d и длиной
L; физические
свойства среды - плотностью
и динамическим коэффициентом молекулярной
вязкости ,
начальные условия отсутствуют, поскольку
рассматривается стационарный случай.
Граничные условия задаются значениями
 и р0
на границах аппарата.
и р0
на границах аппарата.
Задача заключается в решении системы трех дифференциальных уравнений с тремя неизвестными Wx(х,r), Wr(х,r), р(х,r) с целью нахождения полей скоростей и давления:
 (3.37)
(3.37)
Однако, несмотря на все сделанные упрощения, такая система уравнений аналитического решения не имеет, и поэтому используется метод физического моделирования.
Получение критериев подобия. Для получения критериев подобия воспользуемся алгоритмом, изложенным в разд. 3.2.1. Поделим все члены уравнения (3.34) на первый и отбросим символы дифференцирования:
 ,
,
 ,
,
 ,
,
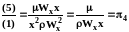 .
.
Поделим все члены уравнения (3.35) на второй:
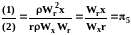 ,
,
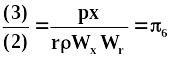 ,
,
 ,
,
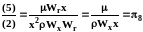 .
.
Поделим первый член уравнения (3.36) на второй:
 .
.
Таким образом, получено 9 критериев подобия. Однако не все из них являются независимыми. Для определения минимального количества критериев воспользуемся -теоремой Бэкингема (разд. 3.2.1). Число величин, между которыми необходимо установить зависимость, N=7 (х, r, , , Wx, Wr, p). Количество величин, обладающих независимыми размерностями, n=3. Допустим это L, W, . Через них можно выразить размерность оставшихся [p] = [] [W]2; [] = [] [W] [L]. Количество величин, обладающих неодинаковой размерностью, Nn=5(L, W, , p). Тогда минимальное количество критериев подобия Nk= N - n = 7 - 3 = 4, из них Ns могут быть симплексами подобия Ns = N – Nn = 7 – 5 = 2.
Общее решение может быть представлено набором различных критериев, учитывая, что комбинация критериев также является критерием подобия. Воспользуемся наиболее употребительными критериями Эйлера (Еu) и Рейнольдса (Rе), а также симплексом подобия S:
 , (3.38)
, (3.38)
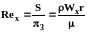 ,
(3.39)
,
(3.39)
 ,
(3.40)
,
(3.40)
 .
(3.41)
.
(3.41)
Нетрудно показать, что все критерии - могут быть получены комбинацией Еu, Reх, Rer, S. В соответствии со второй теоремой подобия общее решение системы дифференциальных уравнений (3.34) - (3.36) может быть представлено в виде зависимости между этими критериями:
 или
или
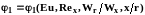 (3.42)
(3.42)
Нами рассмотрен случай ламинарного движения среды. При турбулентном движении в правой части уравнений (3.34) и (3.35) необходимо учесть турбулентный перенос импульса в соответствии с (2.55) с помощью коэффициента турбулентной вязкости т. Поскольку т определяется свойствами среды и полем скорости, то, отбрасывая знаки дифференцирования при получении критериев подобия для гладких (нешероховатых) стенок, его можно представить
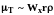 .
.
Так как новых переменных при этом не вводится, то не меняются и критерии подобия (3.38)-(3.41), изменяется лишь конкретный вид зависимости в (3.42), который должен определяться опытным путем. Для шероховатых стенок при значительных числах Reх появляется зависимость т от относительной шероховатости:
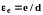 ,
,
 , (3.43)
, (3.43)
где e - средняя высота выступов; n - коэффициент, зависящий от режима движения и характера шероховатости. Нетрудно показать, что введение (3.43) в уравнения (3.38) - (3.41) приведет к появлению дополнительного симплекса подобия e. Однако для упрощения рассуждений мы этот случай рассматривать не будем.
Критерии (3.38)-(3.41) являются локальными, так как составлены из локальных величин, изменяющихся от точки к точке. На практике обычно используют осредненные критерии, состоящие из осредненных величин. Процедуры осреднения могут быть различными, в данном случае удобнее всего усреднять по поперечному сечению аппарата, используя среднюю расходную скорость , тогда
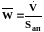 , (3.44)
, (3.44)
 ,
,
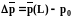 , (3.45)
, (3.45)
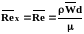 ,
(3.46)
,
(3.46)
 . (3.47)
. (3.47)
Поскольку
аппарат за исключением границ имеет
постоянное сечение Sап,
средняя расходная скорость для любого
внутреннего сечения
будет постоянной величиной, направленной
вдоль оси X
( ).
В силу осесимметричности течения средняя
радиальная составляющая скорости в
любом поперечном сечении равна нулю
).
В силу осесимметричности течения средняя
радиальная составляющая скорости в
любом поперечном сечении равна нулю
 =0,
=0,
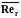 =0.
Давление будет изменяться от сечения
к сечению вдоль оси Х,
но так как интерес обычно представляет
перепад давлений на входе в аппарат и
выходе из него, осредненный критерий
Эйлера записывается относительно р.
=0.
Давление будет изменяться от сечения
к сечению вдоль оси Х,
но так как интерес обычно представляет
перепад давлений на входе в аппарат и
выходе из него, осредненный критерий
Эйлера записывается относительно р.
На
границах аппарата поперечное сечение
имеет иное значение, определяющееся
диаметром входного и выходного штуцеров
d0.
Соответственно иными будут значения
осредненных по данному сечению скорости
и критерия подобия
,
 .
Их можно связать c
.
Их можно связать c
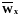 ,
,
 с использованием дополнительного
симплекса подобия:
с использованием дополнительного
симплекса подобия:
 .
.
В соответствии с третьей теоремой подобия явления подобны, если для оригинала и модели равны определяющие критерии подобия и подобны условия однозначности. Но если значения локальных критериев модели и объекта равны в сходственных точках, то при одинаковой процедуре осреднения будут равны и осредненные критерии. Для соблюдения подобия необходимо равенство осредненных определяющих критериев.
Получив
значения определяющих критериев подобия
для объекта - оригинала, например
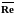 ,
,
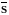 ,
,
 (тогда
(тогда
 следует рассматривать в качестве
определяемого критерия и его значение
будет жестко связано с
,
,
),
а также возможную область их варьирования
в целях оптимизации объекта, следует
приступить к выбору модели.
следует рассматривать в качестве
определяемого критерия и его значение
будет жестко связано с
,
,
),
а также возможную область их варьирования
в целях оптимизации объекта, следует
приступить к выбору модели.
Выбор оптимальной физической модели. Для подобия модели оригиналу необходимо соблюдение подобия условий однозначности, включающих в себя для рассматриваемого примера геометрическое подобие, подобие физических величин и граничных условий (разд. 3.2.1), т.е. модель должна иметь те же пропорции, что и оригинал L/d=idem, d0/d=idem. Кроме того, необходимо подобие поля скоростей во входящих потоках. Равенство скоростей нулю на границе с твердой стенкой будет обеспечиваться автоматически. Размеры модели, выбор
модельных сред и их расходы могут определяться из критерия Rе. Допустим, что оригинал имеет или ориентировочно будет иметь следующие характеристики: d00=0,1м, d0=2 м, L0=5 м, W0=0,1м/с, =2103 кг/м3, =410-3 Пас. Если мы хотим использовать в качестве модельной среды воду (м=103 кг/ м3, м=10-3 Пас), то для соблюдения подобия в модели, уменьшенной в 10 раз по сравнению с оригиналом, средняя расходная скорость должна быть (Rе0=Rем):
 ;
;
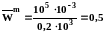 м/с .
м/с .
Уменьшение размеров модели приводит к возрастанию скорости и потерь давления (р), что обусловливает необходимость оптимизации модели путем минимизации суммарных затрат (капитальных и эксплуатационных). Если это возможно, то необходимо предусмотреть диапазон изменений критерия Rе0, а также d00, d0, L0 с целью оптимизации объекта-оригинала. Это потребует проведения экспериментальных исследований в соответствующем диапазоне Rем, Lм/d0м, Lм/dм , для чего следует предусмотреть возможности модельной установки (мощность и производительность насосов, потребности электроэнергии, изготовление моделей различных размеров и т.д.).
