3.5. Моделирование гидродинамической структуры потоков в аппаратах

Как уже отмечалось, наибольший вклад в проблему масштабного перехода вносит изменение гидродинамической структуры потоков при увеличении размеров аппарата, которая в свою очередь влияет на поля температуры и концентраций. Отыскание поля скорости теоретическим путем с использованием исчерпывающего описания вызывает наибольшие математические трудности. Этим объясняется первооче-редное внимание, уделяемое моделированию гидродинамической структуры потоков в аппаратах.

3.5.1. Структура потоков и ее характеристики

Под структурой потока понимают характер движения элементов потока в аппарате. Траектории движения этих элементов могут быть чрезвычайно сложными, что приводит к различному времени их пребывания в аппарате. Одни элементы быстро проходят через аппарат (байпас), другие, наоборот, задерживаются в аппарате на время, значительно больше среднего, так как попадают в участки с малой скоростью движения (застойные зоны), могут также наблюдаться возвратные потоки (рециклы).

Охарактеризовать структуру потоков в аппарате можно полем скорости. Однако теоретическое отыскание поля скорости путем решения системы дифференциальных уравнений, составляющих исчерпывающее описание процессов переноса, для большинства практически важных случаев невозможно, а измерение скоростей в большом количестве точек аппарата представляет значительную техническую сложность. Поэтому в качестве характеристики структуры потока обычно используют время пребывания элементов потока в аппарате. Поскольку различные элементы потока в общем случае имеют различные скорости и траектории движения, то и обладают разными временами пребывания в аппарате. В связи со сложным характером движения и большим числом рассматриваемых элементарных объемов определение конкретного значения времени пребывания отдельного элемента не представляется возможным, и эта величина полагается случайной. Для описания случайных величин используется такая характеристика, как функция распределения.

Величина f(t) называется функцией распределения времени пребывания элементов потока в аппарате. Произведение f(t)dt есть вероятность того, что элементарный объем будет иметь время пребывания в аппарате от t до t+dt, или это есть доля элементов потока, время пребывания которых в аппарате составляет от t до t+dt:

, (3.6)

где dN(t) - количество элементов потока, время пребывания которых в аппарате составляет от t до t + dt; N - общее число выделенных элементарных объемов в аппарате. Из определения (3.6) следует условие нормировки

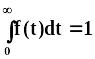, (3.7)

так как вероятность того, что время пребывания элемента потока в аппарате лежит в диапазоне от 0 до , безусловно, равна 1 (100%). Зная функцию распределения f(t), можно найти среднее и наиболее вероятное t_в время пребывания элементов потока в аппарате, t_в соответствует максимальному значению f(t), а

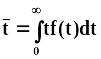. (3.8)

С другой стороны, может быть найдено как

, (3.9)

где V_а - объем аппарата, а - объемный расход (объем среды, проходящий за единицу времени). На рис.3.1 представлен типичный вид функции распределения f(t).

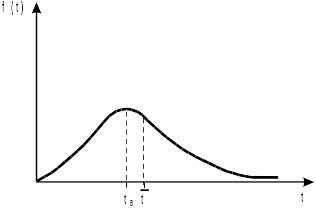
Рис. 3.1. Типичный вид функции распределения элементов потока по времени пребывания в аппарате: t_в - наиболее вероятное, - среднее время пребывания

На практике удобнее использовать безразмерное время пребывания  и безразмерную функцию распределения f*():

, . (3.10)

Произведение f*()d является вероятностью того, что элемент потока будет иметь время пребывания в аппарате от  до +d.