3.4. Сопряженное физическое и математическое моделирование

Основным принципом сопряженного физического и математического моделирования является иерархичность (многоуровневость) пространственно-временных масштабов явлений, протекающих в промышленном аппарате, и, как следствие этого, "слабость" взаимодействия между явлениями различных масштабов. "Слабость" проявляется в отсутствии влияния взаимодействия на структуру математического описания явления, оно может учитываться лишь через изменение некоторых параметров.

С иерархией масштабов мы уже сталкивались при рассмотрении механизмов переноса субстанции. Различие характерных масштабов микро- и макроскопического уровня позволяет учесть их взаимное влияние параметрически через коэффициенты переноса (вязкости, диффузии, температуропроводности). При этом вид математического описания (выражение для потоков за счет молекулярного механизма переноса) остается неизменным. Коэффициенты же переноса (параметры) зависят как от микроскопических характеристик (масса молекул, потенциал взаимодействия), так и макроскопических (поля скорости, температуры, концентраций).

В методе сопряженного физического и математического моделирования аппарат представляется в виде системы, состоящей из характерных зон (областей). Математическое описание каждой зоны устанавливается при ее физическом моделировании на лабораторном макете, при этом оно содержит параметры, учитывающие взаимодействие между зонами. Предполагается, что структура математического описания каждой из зон при изменении масштаба не меняется, меняются лишь значения параметров. Зависимость параметров от масштаба аппарата находится из условия удовлетворения исчерпывающему описанию процессов переноса. С математической точки зрения задача отыскания полей (значений давлений, скоростей, температур, концентраций во всех точках аппарата) заменяется нахождением параметров при известной структуре математического описания, что является значительным упрощением.

В соответствии с вышесказанным поле любой физической величины  (скорости, давления, температуры, концентрации) в каждой из выделенных характерных зон можно представить в виде

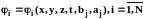, (3.5)

где _i - функция, описывающая поле соответствующей физической величины в i-й зоне аппарата; N - количество характерных зон; x, y, z, t - пространственные и временная координаты; a_j =(a₁ ,a₂ ,a₃ ... a_m) - совокупность параметров, отражающих взаимодействие между зонами; b_j=(b₁ ,b₂ ,b₃ ... b_k ) - совокупность режимных, геометрических и физических величин, входящих в условия однозначности.

При моделировании промышленного аппарата вначале решается задача анализа, а затем синтеза математической модели аппарата. При анализе выделяются характерные зоны (пограничный слой, ядро потока и т.д.), проводится исследование и описание полей в каждой зоне, устанавливаются условия сопряжения на их границах. Структура описания _i в каждой зоне выявляется, как правило, на основе эксперимента, т.е. с использованием физических моделей. Преимущество рассматриваемого метода состоит в том, что исследование и описание каждой зоны может проводиться независимо, т.е. осуществляется физическое моделирование отдельной зоны.

Функции _i , найденные для каждой области аппарата в результате физического моделирования, называют базисными. Базисные функции содержат совокупности параметров a_j. Для моделей областей, на которых проведен эксперимент, параметры - просто числа. При переходе от модели к промышленному аппарату вид базисных функций сохраняется, изменяются лишь значения параметров, учитывающие взаимодействия областей в промышленном аппарате.

Задача синтеза состоит в конструировании математической модели аппарата в целом. При этом требуется обеспечить сохранение структуры базисных функций в определенном диапазоне изменения режимных и конструктивных параметров, а также сопряжение базисных функций путем подстройки параметров a_j. Определение последних в зависимости от масштаба и геометрии аппарата возможно на основе двух подходов: сопоставления расчетных полей с экспериментальными данными для аппарата промышленного масштаба или удовлетворения исчерпывающему математическому описанию. Первый подход требует изготовления аппарата, второй - корректной записи условий однознач­ности и выбора метода подстройки параметров. Второй подход, по-видимому, более предпочтителен.

Если число неизвестных параметров модели и количество уравнений в исчерпывающем описании одинаково, то определение зависимости параметров от размеров аппарата возможно путем интегрирования уравнений по каждой из характерных зон. На практике число искомых параметров, как правило, превышает количество уравнений, тогда для определения параметров может использоваться вариационный метод, заключающийся в отыскании функций, обеспечивающих минимум функционала, составленного в данном случае на основе исчерпывающего описания процессов переноса (подробнее см. в [6] и разд. 3.5.4).

Решение вариационной задачи дает уравнения зависимостей параметров базисных функций от масштаба и геометрии аппарата, обеспечивающих максимальное удовлетворение исчерпывающему описанию.

Таким образом, рассматриваемый метод в отличие от традиционно применяемых упрощенных математических моделей позволяет получить подробное, детальное описание явлений в промышленном аппарате (поле физических величин) со значительно меньшими затратами машинного времени, чем при непосредственном использовании исчерпывающего описания. Данный метод может успешно применяться для оптимизации конструкции аппарата, так как предоставляет возможность анализа последствий различных конструктивных решений. При этом используются уже созданные физические и математические модели характерных зон, пригодные для большинства конструкций.

Можно выделить основные этапы сопряженного физического и математического моделирования:

1) выделение характерных зон аппарата;

2) экспериментальное изучение отдельных зон на физических моделях;

3) составление математических моделей зон; их идентификация по данным физического эксперимента;

4) синтез математической модели аппарата в целом, ее идентификация на основе удовлетворения исчерпывающему описанию;

5) проверка адекватности модели, при необходимости - коррекция;

6) использование модели для проектирования и оптимизации промышленного аппарата.

Преимуществами данного метода являются: возможность физического моделирования отдельных характерных зон аппарата (простота экспериментальных установок, соблюдение подобия); детальное, подробное описание явлений в промышленном аппарате; удобство использования для оптимизации конструкций аппарата; переход к одноуровневой схеме проектирования промышленных аппаратов (лабораторная модель - промышленный аппарат).

К недостаткам метода можно отнести сложность математического аппарата, достаточно большой объем вычислений. Однако их роль существенно снижается за счет использования современных компьютеров и создания вычислительных комплексов, объединенных в систему автоматизированного проектирования.