2.2. Закон сохранения энергии

Суть закона сохранения энергии состоит в том, что энергия не может исчезать либо возникать, она лишь переходит из одного вида в другой. Таким образом, суммарная энергия изолированной системы есть величина постоянная (изолированная система не обменивается с окружающей средой массой и энергией, не находится под воздействием внешних сил), т.е. или . Рассмотрим закон сохранения энергии для неизолированной системы.

2.2.1. Интегральная форма закона сохранения энергии

(первый закон термодинамики)

В общем случае закон сохранения энергии в интегральной форме можно сформулировать аналогично закону сохранения массы: изменение энергии в системе вызывается разностью прихода и расхода энергии. Учитывая, что энергия может передаваться в форме теплоты и работы (см. разд. 1.3.2.), можно записать

, или . (2.31)

Это есть ни что иное, как первый закон термодинамики: если от окружающей среды системе передается некоторое количество энергии в форме теплоты , то часть ее расходуется на производство работы , а другая идет на увеличение энергии системы 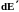. Поскольку энергия характеризует свойства системы, то ее изменение является полным дифференциалом и обозначается . Теплота и работа характеризуют связь системы с окружающей средой и их изменение не является полным дифференциалом, это отражается в обозначениях и . Отметим, что, как и в разд. 1.3.2, все величины, обозначенные штрихами, отнесены к единице массы системы и измеряются в Дж/кг. Положительной принято считать работу, совершаемую системой (А_расх), а отрицательной - работу совершаемую над системой (А_пр), этим объясняется знак “ - ” перед в (2.31).

Как уже отмечалось в 1.3.2, полная энергия системы Е складывается из внутренней U, кинетической Е_k и потенциальной Е_п (последние два вида энергии носят название механической). Учитывая наиболее распространенный случай потенциальной энергии в поле сил тяжести , можно представить полную энергию следующим образом:

. (2.32)

Работа может совершаться движущейся средой по преодолению сил внешнего давления и трения (работа проталкивания):

, (2.33)

где - объем, приходящийся на единицу массы, т.е. величина обратная плотности . С учетом этого уравнение (2.31) можно переписать

(2.34)

или, введя понятие энтальпии,

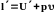(2.35)

. (2.36)

Рассмотрим частные случаи закона сохранения энергии. Например, для изотермической идеальной жидкости, движущейся без трения и теплообмена с окружающей средой , , , уравнение (2.34) будет иметь вид

. (2.37)

После интегрирования получаем уравнение Бернулли, выражающее закон сохранения механической энергии единичной массы:

. (2.38)

Вернемся к уравнению (2.36). При постоянстве механической энергии Е_k+Е_п=const (нагрев вязкой среды при протекании ее по горизонтальному каналу постоянного сечения) оно будет иметь вид

. (2.39)