Общая характеристика структурных компонентов. Отношения: связи
Отношение есть агрегат множеств. Само отношение также является множеством. Поэтому можно рассматривать агрегат отношений.
Определение
Агрегат, построенный на других отношениях, рассматривается как связь между этими отношениями.
Для таких агрегатов, наряду с интенсионалом и экстенсионалом, рассматривается еще одно важное свойство отношений – отображение между отношениями, на которых построен агрегат.
Без потери общности, ограничимся рассмотрением бинарных отношений – отношений, построенных на двух множествах.
Рассмотрим бинарное отношение связи R, построенное на двух множествах – отношениях сущностей S1 и S2: R = {<s1i, s2j> | s1i ∈ S1, s2j ∈ S2}. Данное отношение связи определяет два отображения:
прямое – R : S1 S2
обратное – R-1 : S2 S1
Важной характеристикой отображения является кардинальное число.
Определение
Кардинальное число отображения определяется количеством элементов одного множества, связанных с одним элементом другого множества.
Так, для прямого отображения R : S1 S2, кардинальное число определяется количеством элементов множества S2, связанных с одним элементом множества S1; для обратного отображения R-1 : S2 S1 – количеством элементов множества S1, связанных с одним элементом множества S2.
Так как с разными элементами одного множества может быть связано разное количество элементов другого множества, отображения обычно характеризуются минимальным и максимальным кардинальными числами. Поскольку отношение связи определяет два отображения, используется следующая нотация:
R ( S1 (m1, n1) : S2 (m2, n2 ) )
Запись S1 (m1, n1) определяет минимальное (m1) и максимальное (n1) кардинальные числа отображения S2 S1. Соответственно, запись S2 (m2, n2) определяет минимальное (m2) и максимальное (n2) кардинальные числа отображения S1 S2.
Смысл такой записи:
каждый элемент из S1 связан минимум с m2, максимум с n2 элементами из S2,
каждый элемент из S2 связан минимум с m1, максимум с n1 элементами из S1.
Если на отображения не наложены никакие ограничения, считается, что минимальное и максимальное кардинальные числа не определены: R ( S1 ( 0, ∞ ) : S2 (0, ∞ ) ), или R ( S1 : S2 ). Это означает, что элемент из S2 может быть связан с любым количеством элементов из S1, и наоборот.
Наложив те или иные ограничения на минимальное и максимальное кардинальные числа, можно получить различные типы отображений. Пусть, например, определены сущности СТУДЕНТ и КУРС (курс по выбору). Каждый студент должен выбрать один из курсов, но не более трех. На каждый курс должны быть зачислены не менее 5 и не более 100 студентов. Тогда получаем следующее отношение связи:
ВЫБИРАЕТ ( СТУДЕНТ (5, 100) : КУРС (1, 3) ).
Рассмотрим некоторые особые типы отображений.
Пусть имеем следующее отношение связи: R ( S1 ( 0, ∞ ) : S2 (1, ∞ ) ). Рассмотрим отображение S1 S2. Минимальное кардинальное число данного отображения равно 1. Это означает, что каждый элемент из S1 связан, по крайней мере, с одним элементом из S2 (или отображается, по крайней мере, одним элементом S2). Такое отображение называется полностью определенным на S1, а соответствующее ограничение называется ограничением по существованию: для существования объекта в S1 необходимо, чтобы он был связан с объектом из S2 (Рис. 2.3).
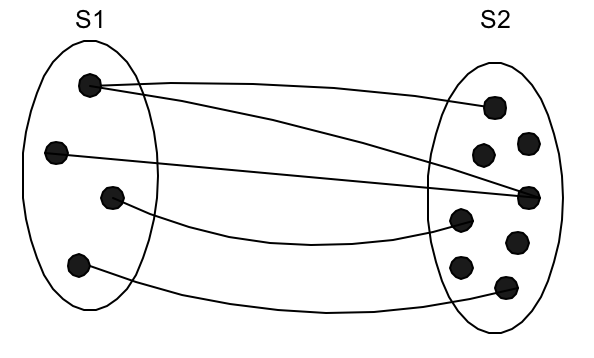
Рис. 2.3. Полностью определенное отображение на S1
Пусть имеем следующее отношение связи: R ( S1 ( 0, ∞ ) : S2 ( 0, 1 ) ). Рассмотрим отображение
S1 S2. Максимальное кардинальное число данного отображения равно 1. Это означает, что каждый элемент из S1 связан не более чем с одним элементом из S2 (или отображается не более чем одним элементом S2). Такое отображение называется неполным функциональным отображением, так как минимальное кардинальное число отображения равно 0, т.е. не все элементы из S1 отображаются в S2 (Рис. 2.4).
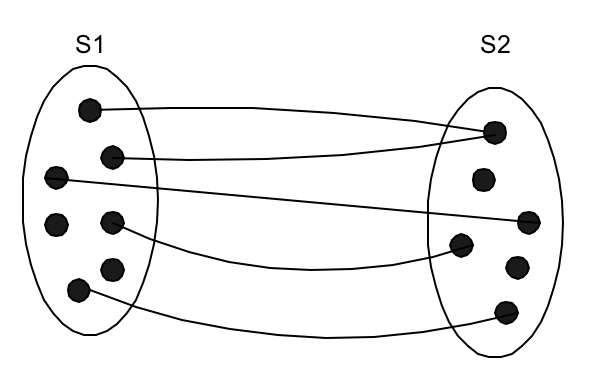
Рис. 2.4. Неполное функциональное отображение
Пусть имеем следующее отношение связи: R ( S1 ( 0, ∞ ) : S2 ( 1, 1 ) ). Рассмотрим отображение
S1 S2. И минимальное, и максимальное кардинальные числа данного отображения равны 1. Это означает, что каждый элемент из S1 связан в точности с одним элементом из S2 (или отображается точно одним элементом S2). Такое отображение называется полным функциональным отображением (Рис. 2.5).
Рис. 2.5. Полное функциональное отображение
Связи, для которых хотя бы одно отображение является функциональным (полным или неполным), часто называют связями типа 1 : n, или «один ко многим». Связи, в которых оба отображения являются нефункциональными, называют связями типа n : n, или «многие ко многим».