Бинарные деревья
Прежде всего, рассмотрим двоичные (или бинарные) деревья поиска. Они могут обеспечить разумный компромисс и для произвольной, и для последовательной выборки данных.
Бинарное дерево поиска представляет собой упорядоченную тройку (TL, R, TR), где R – корневая вершина дерева, TL, TR – левое и правое поддеревья вершины R, соответственно.
Каждое из поддеревьев может быть пустым или представляет собой такое же бинарное дерево. TL и TR содержат, соответственно, NL и NR вершин, NL ≥ 0, NR ≥ 0. Общее количество записей в бинарном дереве NR = NL + NR + 1.
Бинарное дерево поиска на множестве NR ключей есть бинарное дерево TNR, в котором каждая вершина помечена отдельным ключом и расположена в соответствии с определенным порядком ключей. Для любой вершины i ключи вершин в его левом поддереве «меньше» ключа вершины i, который, в свою очередь, «меньше» ключей вершин в его правом поддереве.
В каждой вершине бинарного дерева должны храниться:
значение вершины, т.е. значение полного первичного ключа и некоторая запись RowId, указывающая на размещение соответствующей строки таблицы,
левый и правый указатели на поддеревья.
Механизм поиска очевиден.
При анализе алгоритма поиска определяют длину пути до целевой записи как количество просмотренных вершин дерева от корня до целевой вершины.
Вставка в бинарное дерево проста, но при этом можно получить разные формы дерева – от линейного списка (Рис. 7.2, а) до сбалансированного дерева (Рис. 7.2, б). Наиболее часто встречается нечто среднее между этими двумя крайними случаями (Рис. 7.2, в).
Рис. 7.2. Примеры бинарных деревьев
Введем некоторые определения.
1. Уровень вершины или листа i, обозначаемый Li, определяется длиной пути от корневой вершины TNR до вершины i.
Корневая вершина, по определению, имеет уровень 0.
2. Высота дерева определяется как максимальный уровень среди всех вершин дерева.
3. Бинарное дерево называется сбалансированным, если разница уровней любых двух листьев не превышает 1.
Использование сбалансированного дерева минимизирует среднюю длину доступа.
Неудобство бинарных деревьев поиска заключается в том, что они слишком «высокие»; требуется просмотреть достаточно большое количество вершин дерева, прежде чем будет найдена искомая.
Операции поиска и вставки (в несбалансированное дерево) очевидны.
С операцией удаления связаны определенные проблемы.
Удаление листа выполняется просто.
При удалении промежуточной вершины необходимо сохранить упорядоченность вершин дерева. Возможны разные алгоритмы удаления; например, на место удаляемой промежуточной вершины перемещается элемент с минимальным значением ключа из правого поддерева, подчиненного удаляемой вершине (Рис. 7.3).
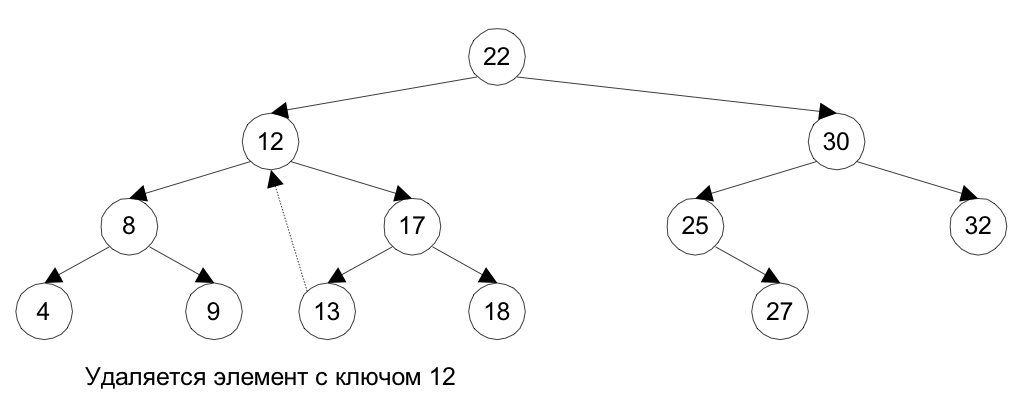
Рис. 7.3. Пример удаления элемента из бинарного дерева
Удаление промежуточной вершины может потребовать реорганизации нескольких уровней бинарного дерева.
На практике бинарные деревья поиска применяются крайне редко, так как из-за своей «высоты» требуют много обращений к внешней памяти при поиске.