9.5. Геометричні тіла

У 5-7-му класах розумово відсталі школярі повторюють матеріал про геометричні тіла, які вони вивчали у молодших класах. При цьо­му вчитель звертає увагу на їхні вершини, грані і сторони, знову ж та­ки повертається до пояснення їх властивостей. Він проводить порівняння геометричних фігур і геометричних тіл використовуючи практичну діяльність учнів. При цьому він пояснює, що геометрична фігура має два виміри - довжину і ширину, і коли її покласти на пло­щину стола - вона цілком належить даній площині. У той же час гео­метричне тіло має три виміри - довжину, ширину і висоту, і коли його покласти на площину стола, воно виступає над його поверхнею, тобто не належить повністю його площині.

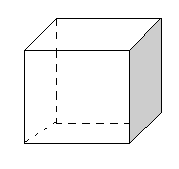
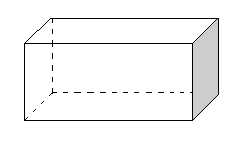
Починаючи з 8-го класу основна увага на уроках приділяється ор­ганізації роботи з геометричними тілами. Причому почати потрібно з формування у школярів поняття про многогранник. Вчитель порів­нює його з багатокутником. Він пояснює, що багатокутник означає геометричну фігуру, яка характеризується лише шириною і довжи­ною і розміщується на площині так, що належить їй, а многогранник - це геометричне тіло, яке складається з багатьох гра­ней і розміщується на площині так, що не належить їй, оскільки крім ширини і довжини має ще й висоту. Вчитель дає визначення: многогранник - це тіло, обмежене скінченою кількістю площин. Межею многогранника є його поверхнею. Бажано показати різницю між ни­ми на рисунка, використати макети многогранників і багатокутників (див. рис. 9.40.).

Рисунок 9.40.

Многогранники Багатокутники

Після розповіді робиться коротка характеристика многогранника: гранями називаються частини площини (багатокутники), які обмежу­ють його; ребра - це спільні сторони суміжних граней (багатокутни­ків); вершини - це точки, які утворюються його гранями, що сходяться в одній точці. У 8-му класі педагог вводить у словник дітей такі поняття, як куб і прямокутний паралелепіпед. Відповідно до програми вони вчаться обчислювати площу однієї грані, бічної і повної поверхні цих геомет­ричних фігур у 4 чверті. Почати формування цих вмінь доцільно з ха­рактеристики куба:

1. У куба 6 граней, всі вони квадрати і рівні між собою.

2. У куба 12 ребер, які рівні між собою.

3. У куба 8 вершин.

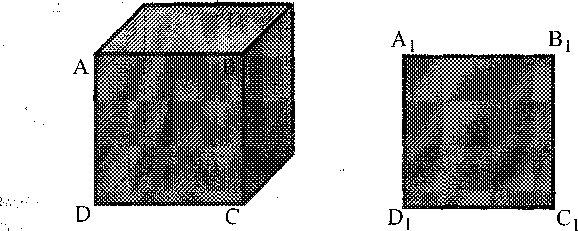
Для закріплення цього матеріалу потрібно роздати школярам ку­бики і перерахувати грані, ребра і вершини. Педагог проводить порів­няння квадрата і куба для того, щоб учні надалі не змішували ці фігури між собою. Таке порівняння дасть змогу пояснити, що бічна поверхня куба (або його грань) є квадратом, тобто геометричною фі­гурою, у якої всі кути прямі, а сторони рівні між собою. Виконавши вимірювання кутів і сторін на одній з граней куба, сторін і кутів квад­рата вони пересвідчуються, що грань АВСD у многограннику і квад­рат А₁В₁С₁D₁ між собою рівні (див. рис. 9.41.).

Рисунок 9.41.

М N

Ці вправи виступають пропедевтичними для формування обчис­лення спочатку бічної, а потім повної поверхні куба. Цей матеріал не є складним і розумово відсталі учні оволодівають ним порівняно швидко.

Вчитель спочатку пояснює алгоритм визначення площі бічної по­верхні куба. Для цього школярі беруть куб, виготовлений з пластмаси або дерева і обводять його грань на папері. Після цього вимірюють сторони квадрата, який при цьому утворився і обчислюють за форму­лою: S_КВ = 2а.

Познайомившись з обчисленням площі бічної поверхні куба педа­гог переходить до формування вміння обчислювати площу його по­вної поверхні. Для кращого розуміння матеріалу вчитель виготовляє куб з цупкого паперу. Після цього він його розрізає або розкладає, (тобто робить його розгортку) і пронумеровує всі грані, визначаючи їхню кількість (див. рис. 9.42.).

Рисунок 9.42.

2
3	4	5	6
1

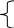
2 см

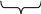
2 см

Виконавши таку практичну роботу проводить обчислення:

1. 2 см · 2 см = 4 см² – площа однієї бічної грані куба.

2. 4 см² · 4=16 см² – площа бічної поверхні куба.

3. 4 см² · 6 = 24 см² – площа повної поверхні куба.

Формуючи ці знання та вміння вчитель прагне домогтись усвідом­лення школярами, чому для визначення бічної поверхні куба потріб­но площу грані множини на 4, а для обчислення його повної площі – на 6.

Після цього починається засвоєння знань про паралелепіпед. Вчи­тель дає визначення: паралелепіпед - це геометрична фігура, гранями якого є інші геометричні фігури - паралелограми. Паралелепіпед, основами якого є прямокутники, називається прямокутним. На прикла­ді сірникової коробки вчитель пояснює, що поверхня прямокутного паралелепіпеда складається з 6-ти прямокутників. Довжина кожного з трьох ребер, які виходять з однієї точки, називається виміром паралелепіпеда.

У 9-му класі учні знайомляться з деякими властивостями парале­лепіпеда:

1. У паралелепіпеда 6 граней: 2 основи - верхня і нижня, 4 - бічні.

2. Основи паралелепіпеда мають форму прямокутників або квадратів.

3. Бічні грані паралелепіпеда мають форму прямокутників.

4. Протилежні грані паралелепіпеда паралельні і рівні між собою.

5. У паралелепіпеда 12 ребер і 8 вершин.

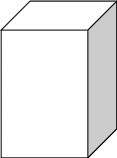
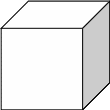
Вчитель проводить порівняння куба і паралелепіпеда, вказуючи на їхні основні відмінності. Таку роботу потрібно провести на моделях і рисунках цих тіл (див. рис. 9.43.).

Рисунок 9.43.

2 см 2 см

2 см 6 см

2 см

3 см

Головне при цьому - сформувати уявлення, що у куба всі грані і сторони рівні, а в паралелепіпеда - ні, оскільки він утворений з пря­мокутників. Для порівняння куба і паралелограма також можна ви­користати таблицю (див. табл. 9.6.).

Таблиця 9.6.

Геометричне тіло	Вершини	Грані	Ребра
Куб	8 вершин	6 граней. Протилежні між собою. Усі грані – квадрати.	12 ребер. Протилежні ребра і грані паралельні. Всі ребра рівні між собою.
Паралелепіпед	8 вершин	6 граней. Протилежні грані паралельні між собою. Усі грані – прямокутники або 2 грані – квадрати, 4 – прямокутники.	12 ребер. Протилежні ребра і грані паралельні і рівні між собою.

У цей період уточнюються положення одних граней по відношен­ню до інших. Термін "протилежні сторони" вже знайомий школярам і тепер вони вчаться виділяти протилежні грані. Для цього кожен учень повинен мати куб і прямокутний паралелепіпед з гранями, на яких стоять номера. Вчитель організовує роботу з виділення суміж­них (ті, які знаходяться поряд) і протилежних граней. Розумово від­сталі повинні усвідомити, що суміжні грані ні в якому разі не можуть бути протилежними, а протилежні - суміжними.

Познайомивши школярів з основним властивостями куба і прямо­кутного паралелепіпеда і склавши таблицю порівняння цих геометричних тіл вчитель пояснює, як визначається його бічна і повна поверхня, використовуючи правило: бічною поверхнею паралелепі­педа є сума площ всіх його бічних граней; повною поверхнею пара­лелепіпеда є сума площ всіх його граней. Обчислення бічної і повної його площі відбувається так само, як і квадрата. Але педагог повинен зазначити, що у даної фігури грані можуть бути одночасно квадрати і прямокутники або прямокутники з різною довжиною сторін. Тому потрібно це враховувати виконуючи обчислення повної площі прямо­кутного паралелепіпеда.

Знайомлячи їх з поняттям "об'єм" вчитель пояснює, що коли одну і ту саму банку заповнити різними рідинами, то їхня маса буде різ­ною (водою, медом, бензином), а об'єм залишиться той самий. Тобто це поняття в будь-якій посудині показує її місткість. Дві посудини мають один і той самий об'єм, якщо рідина, яка повністю заповнює одну з них, після переливання повністю заповнює іншу. Цю роботу потрібно унаочнювати безпосередньо дослідом: перелити 1 літр води у 2 півлітрові банки; налити 1 літр води і 1 меду у літрові банки, а по­тім зважити їх тощо.

Дається визначення: об'ємом геометричного тіла називається ве­личина частини простору, яку займає це тіло.

Після проведення таких експериментів вчитель пояснює, що об'єм, так само як і площа, може вимірюватись. Для вимірювання об'єму використовуються відповідні міри. Далі він повторює вже ві­домі учням міри довжини і площі і співставляє їх з об'ємом. Педагог пояснює, що так само, як довжина і площа вимірюється у сантимет­рах та, відповідно, у сантиметрах квадратних об'єм також має свій вимір. Він зупиняється на тому, що для вимірювання довжини вико­ристовують одну величину – довжину, і позначають її в сантиметрах; для вимірювання площі використовують дві величини - довжину і ширину, і для позначення цієї міри беруть сантиметри квадратні. Піс­ля цього вія пояснює, що для вимірювання об'єму використовують три величини - довжину, ширину і висоту, і познають її в сантиметрах кубічних (см³). Для підтвердження своїх слів він пропонує розглянути відповідний рисунок (див. рис. 9.44.):

Рисунок 9.44.

д овжина площа об'єм

Перший раз для обчислення об'єму доцільно взяти прямокутний паралелепіпед, довжина сторін якого дорівнює 4 см, 3 см, 2 см. Уч­ні вимірюють висоту, ширину, довжину такої фігури, а потім рахують кубики з довжиною сторін 1 см, які в неї входять. Порахувавши куби­ки отримують число 24. Паралельно вчитель вводить правило: щоб знайти об'єм прямокутного паралелепіпед потрібно його довжину помножити на висоту і на ширину. Так само, як для визначення пери­метра та площі для вимірювання об'єму також використовують фор­мулу. Об'єм позначається латинською літерою V. Оскільки для визначення об'єму перемножуємо три сторони - ширину, довжину і висоту (а·b·с ), то обчислення об'єму цього прямокутного паралелепі­педа виконується таким чином: V = а·b·с. Якщо для обчислення площі ми беремо добуток двох сторін і позначаємо його у см³, то оскільки для обчислення об'єму ми беремо добуток трьох сторін – його потрібно позначати у см³.

Сформувавши в розумово відсталих учнів вміння обчислювати об'єм прямокутного паралелепіпеда можна пояснити їм, що куб - це особливий випадок прямокутного паралелепіпеда, всі сторони якого рівні між собою. Отже, щоб обчислити об'єм куба, потрібно його до­вжину помножити на висоту і ширину. Оскільки довжина всіх сторін куба однакова і дорівнює, наприклад, 3см, то для того, щоб визначи­ти його об'єм, потрібно використати формулу: V = а·b·b(3 см · 3 см · 3 см = 27 см ). Тільки в цьому випадку вона набирає ви­гляду V = а-а-а. Лише після того, як учні засвоїли обчислення фігур у см , можна переходити до пояснення того, що при обчисленні об'єму використовують також дециметри (дм ) і метри (м ).

Для закріплення цього матеріалу можна скласти разом з учнями таблицю співвідношення лінійних, квадратних і кубічних мір (див. табл. 9.7.).

Таблиця 9.7.

міри довжини	міри площі	міри об’єму
1 м = 10 дм 1 м = 100 см 1 дм = 10 мм	1 м2 = 100 дм2 1 м2 = 10 000 см2 1 дм2 = 100 см2 1 см2 = 100 мм2	1 м 3 = 1000 дм3 1 м 3 = 1 000 000 см3 1 дм 3 = 1000 см3 1 см 3 = 1000 мм3

Для того, щоб вони краще засвоїли ці поняття доцільно викорис­товувати моделі кубічних дециметрів (а, по можливості, і метрів), на гранях яких є розмітка відповідно у сантиметрах та дециметрах.

Підсумовуючи можна сказати, що у останніх трьох темах ми праг­нули розглянути якомога більше питань про методику вивчення гео­метричного матеріалу розумово відсталими учнями у допоміжній школі. Для їх повного і докладнішого висвітлення потрібно значно більше часу.

Контрольні запитання

1. В чому полягає значення вивчення властивостей ліній і кутів для вивчення геометричного матеріалу в старших класах допоміжної школи?

2. Які властивості трикутників вивчають учні допоміжної школи?

3. Поясніть методику знайомства розумово відсталих учнів з об­численням площі.

4. З якими геометричними тілами знайомляться школярі в стар­ших класах? Які властивості цих тіл вони вивчають?

5. В якій послідовності доцільно знайомити учнів з обчисленнями об'єму?

6. Обґрунтуйте доцільність використання пам'яток на уроках ви­вчення геометричного матер1алу у старших класах?

Рекомендована литература

1. Демидова М.Е. Работа с геометрическим материалом в школе VIII вида / Демидова М.Е. // Дефектология. - 2002. - №1. - С.51-60.

2. Книга для учителя вспомогательной школы / [Под ред. Г.М.Дульнева]. - М.: Учпедгиз, 1959.

3. Кузьмина-Сыромятникова Н.Ф. Методика арифметики во вспомогательной школе / Кузьмина-Сыромятникова Н.Ф.. - М.: Учпедгиз, 1949.

4. Перова М.Н. Методика преподавания математике в специаль­ной (коррекционной) школе VIII вида / Перова М.Н.. - М.: Владос, 1999.

5. Перова М.Н. Изучение взаимного положения геомет­рических фигур на плоскости на уроках математики во вспомогатель­ной школе / М.Н.Перова, В.В.Эк // Дефектология. - 1982. - №1. - С.29-36.

6. Попович СМ. Состояние знаний учащихся вспомогательной школы о существенных признаках геометрических фигур / Попович СМ. // Дефекто­логия. - 1982. - №6. - С.33-36.

7. Попович СМ. Шляхи вивчення геометричних фігур в допоміжній школі / Попович СМ. [методичний лист / За ред. Г.М.Мерсіянової]. - К.: Радянська школа, 1967. -46с.

8. Тишин П.Г. Обучение учащихся вспомогательной школы на­глядной геометрии / Тишин П.Г. // Известия АПН РСФСР. - 1952. - Вып. 41. -С.79-164.

9. Эк В.В. Обучение наглядной геометрии во вспомогательной школе / В.В.Эк, М.Н.Перова. - М.: Просвещение, 1983.