9.3. Трикутник

Учні допоміжної школи в молодших класах знайомляться з трику­тником як із фігурою, яка має певну форму, вчаться виділяти його в навколишніх предметах.

Розумово відсталі учні старших класів починають знайомство з трикутником з усвідомлення поняття "площина". Педагог розповідає, що площину можна собі уявити, розглядаючи поверхню стола, дзер­кала, поверхню спокійної води в посудині, на ставку в безвітряну по­году. Можна запропонувати дітям самостійно навести ще декілька прикладів площин - стіна, вікно, підлога тощо.

„Аркуш паперу, який лежить на парті, також є площиною. Накрес­лимо на ньому замкнуту ламану лінію з трьох відрізків. Ми дістане­мо частину площини, обмежену цією ламаною. Я ставлю запитання: "Яку фігуру нагадує нам ця ламана лінія?" (Трикутник). Отже, трику­тник - це фігура, утворена замкнутою ламаною, яка складається з трьох ланок". Таке пояснення буде найбільш доступним для розумо­во відсталих.

Формування в учнів вміння креслити трикутники без опори на то­чки вчитель починає з прямокутного, оскільки його найлегше накрес­лити використовуючи косинець і діти на ньому вже визначають прямий кут. Побудувавши прямий кут учні на його сторонах довільно відкладають дві точки і з'єднують їх між собою. При цьому прямий кут на дошці бажано виділити кольоровою крейдою, а в зошиті - ко­льоровими олівцями. Так само він пояснює креслення тупокутного трикутника.

Останнім учні вчаться будувати гострокутний трикутник. Його важко креслити - не можна почати з гострого кута, адже може стати­ся так, що один із кутів буде тупим або прямим. Учитель знає, що завжди гострокутним є трикутник, всі сторони якого рівні. Тому, не використовуючи слово "рівносторонній", він пояснює це учням і розповідає про послідовність його побудови за допомогою циркуля та лінійки (див. рис. 9.26.).

Рисунок 9.26.

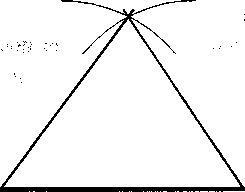
Якщо школярі оволоділи навичками побудови трикутників вчи­тель дає визначення: трикутник - це частина площини, обмежена трьома відрізками прямих (або сторонами), дві з яких мають по одній спільній вершині. При цьому він обов'язково показує все, що зобра­жено на рисунку: частину площини, яка знаходиться в середині лама­ної, замкнену ламану з трьох відрізків, вершини. Це необхідно зробити, адже у розумово відсталих часто трапляються випадки по­рушення взаємозв'язку між словом і образом. Під час знайомства з трикутником доцільно виконати його рисунок з позначенням словами елементів, які його утворюють (див. рис. 9.27.).

Рисунок 9.27.

В

б ічна сторона бічна сторона

п лощина

А основа С

вершини трикутника

Перше знайомство з типами трикутників за величною кутів розу­мово відсталі отримують у 4-му класі. Завдання вчителя в 7-му класі - закріпити ці знання і навчитись використовувати їх у практич­ній діяльності.

Усвідомлення розумово відсталими однієї з основних властивос­тей трикутника - його висоти - одне з головних завдань, яке стоїть перед вчителем. Він зазначає, що найлегше її провести в гострокут­ному трикутнику за допомогою косинця. Для цього педагог вчить прикладати його до трикутника так, щоб одна сторона лежала на його основі, а друга проходила через вершину, протилежну їй (див. рис. 9.28.).

Рисунок 9.28.

вершина

в исота

основа

Р исунок 9.29.

h

Після цього він дає визначення, що опущений з вершини трикут­ника на основу перпендикуляр називається його висотою. Для закріп­лення цього вчитель показує це на трикутниках, накреслених на дошці, вирізаних з паперу, складених із паличок тощо. Він також вказує, що висоту трикутника (як будь-якої іншої геометричної фігури) прийнято позначати латинською літерою h.

Проведення висоти зустрічає найбільше труднощів під час органі­зації роботи з тупокутним трикутником. Розумово відсталі довго не можуть усвідомити, що для її побудови у цій фігурі потрібно винести косинець за межі його площини, провівши для цього допоміжну лі­нію, яка при цьому не змінює конфігурацію самої геометричної фігу­ри (див. рис. 9.29.). Враховуючи це вчитель повинен відвести на цю роботу достатню кількість часу, звернути на нього більше уваги й ор­ганізувати практичні заняття.

Також у розумово відсталих важко формується поняття, що висота у прямокутному трикутнику співпадає з його бічною стороною. Для того, щоб школярі краще усвідомили цей матеріал, потрібно провес­ти докладне його пояснення з використанням виготовлених на уроках ручної праці, трудового навчання прямокутних трикутників. Бажано, щоб вони були такої величини, яка б дозволяла учням провести по­рівнювання їх зі своїм зростом. Ставлячи їх на основу вони повинні на практиці переконатись, що висота трикутника дорівнює відстані від його основи до вершини, тобто до найвищої його точки. Якщо взяти прямокутній трикутник з різною довжиною сторін, наприклад З см і 2 см, то у випадку, коли його основа - 3 см, висота буде, відпо­відно, 2 см, і навпаки, якщо основа - 2 см, то висота, відповідно, 3 см (див. рис. 9.30.).

Рисунок 9.30

А А

h h

В С В С

На рухомих моделях можна наочно показати, як розташована ви­сота в різних трикутниках. Ці вправи спрямовані на закріплення матеріалу.

Після знайомства з типами трикутників і формуванням вміння проводити у них висоту потрібно організувати порівняння прямокут­ного трикутника й прямокутника. Подібність у звучанні назв призво­дить до того, що школярі часто змішують їх, губляться, інколи взагалі відмовляються працювати, якщо ці знання недостатньо диференційо­вані. Тому необхідно показати їхню схожість і відмінність. Це знову ж таки доцільніше всього зробити під час виконання практичних за­вдань. Для того, щоб школярі навчились їх розпізнавати, потрібно ви­різати два різнокольорові прямокутні трикутники. Учні позначають їх: ∆АВБ, ∆АОС. Після цього вони утворюють із них прямокутник АВСD. Розкладаючи і складаючи дану фігуру у них створюється чітка диференціація прямокутного трикутника і прямокутника (див. рис. 9.31.).

Рисунок 9.31

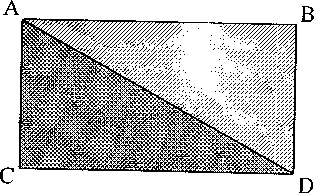
Під час вивчення й закріплення цього матеріалу доцільно проана­лізувати кількість прямих і гострих кутів у прямокутнику і прямокут­них трикутниках, які його утворюють. Школярі повинні визначити, що в цих трикутниках є один кут прямий і два гострі. Вчитель звертає увагу, що для утворення прямокутника трикутники повинні мати не лише одну спільну ознаку кутів (один прямий кут і два гострі), але й спільну ознаку сторін (довжина їх повинна бути однакова). Для кра­щого усвідомлення властивостей, необхідних для побудови прямокутника, педагог пропонує скласти його з двох прямокутних трикутників, які мають при цьому різні довжини сторін; із двох гост­рокутних, тупокутних трикутників. Школярі на практиці перекону­ються у неможливості цього зробити.

Формуючи вміння розрізняти трикутники за довжиною сторін та­кож доцільно з практичної роботи: вчитель ставить завдання досліди­ти довжини всіх сторін різних трикутників. Проводячи ці вимірювання учні переконуються, що одна група трикутників має сторони однакової довжини, друга - дві сторони однакової довжини, у третьої групи всі три сторони мають різну довжину. Після виконан­ня цих завдань педагог робить висновок: за довжиною сторін трикут­ники діляться на три типи: різносторонні, рівнобічні і рівносторонні. Він дає визначення: трикутник називається рівно стороннім, якщо всі три сторони, які його утворюють, рівні; рівнобічним називається трикутник, у якого дві сторони рівні; якщо всі сторони трикутника ма­ють різну довжину він називається різносторонній.

Для закріплення цих знань учні креслять у себе в зошитах таблиці і заповнюють їх відповідними рисунками. При цьому педагог контро­лює їхню роботу, адже деякі з них можуть не зорієнтуватись у вели­чині відповідних креслень (див. табл. 9.1., 9.2.).

Таблиця 9.1.

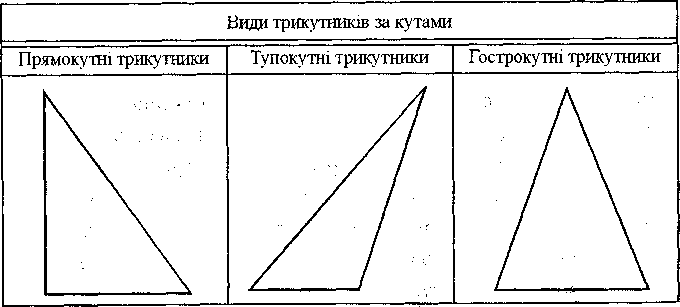
Таблиця 9.2.

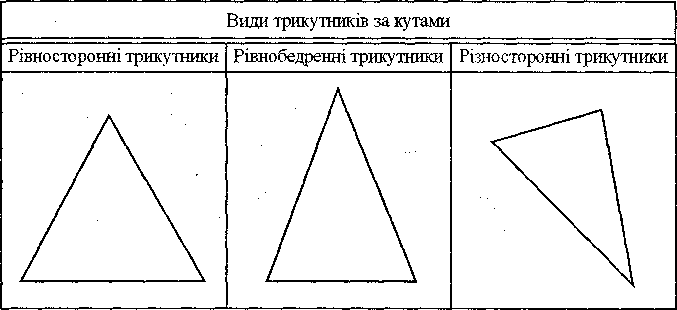
Після розгляду матеріалу про основні типи трикутників вчитель знайомить школярів з побудовою трикутника, якщо відомі довжини всіх його сторін. Для цього доцільно використати пам'ятку:

1. Виміряй першу сторону, якe ти береш за основу і накресли її.

2. Візьми циркуль і виміряй ним другу сторону.

3. Постав ніжку циркуля на початок відрізка, якого ти прийняв за основу і з того боку, де плануєш креслити фігури, проведи півколо.

4. Виміряй третю сторону циркулем.

5. Постав ніжку циркуля у кінцеву точку відрізка, якого ти прийн­яв за основу і проведи півколо таким чином, щоб воно перетнулось з першим півколом.

6. Постав у цьому місці точку.

7. Сполучи точки відрізка, прийнятого за основу, з точкою, яка утворилась після перетину двох півкіл. Ти отримав трикутник зада­них розмірів. Виконай перевірку.

Бажано, щоб вона була підкріплена відповідним рисунком (див. рис. 9.31.).

С Рисунок 9.31.

С

А В А В А В

У процесі роботи вчитель уважно слідкує за учнями і у випадку необхідності надає допомогу. Він вимагає від них дотримання прави­льної послідовності побудови та розміщення рисунка.

У цьому класі учні повинні взнати про ще одну властивість сторін даної геометричної фігури: у будь-якого трикутника довжина однієї сторони повинна бути меншою за суму двох інших і більшою за їх­ню різницю. Це правило розумово відсталі спочатку вивчають напа­м'ять, а потім закріплюють, виконуючи практичні вправи:

1. Чи можна побудувати трикутник за довжинами сторін - 6 см, 7 см, 8 см? 6 см, 2 см і 3 см? 9 см, 5 см і 4 см?

2. Назвіть довжини сторін, за якими можна побудувати трикутник?

3. Назвіть довжини сторін, за якими не можна побудувати трикутник?

4. Довжина двох відрізків 5 см і 6 см. Підберіть довжину третього так, щоб можна було з них побудувати трикутник?

5. Довжина двох відрізків 5 см і 6 см. Підберіть довжину третього так, щоб не можна було побудувати трикутник?

У цей же час школярі вивчають, що форма трикутника, складеного із паличок, закріплених шарнірно, не змінюється, тоді як фігури пря­мокутної і квадратної форми легко змінюються.

У 7-му класі учні приходять до висновку, що сума кутів трикутни­ка дорівнює 180°. Для цього можна використати і дедуктивний, і ін­дуктивний шлях пізнання.

У першому випадку педагог зразу повідомляє цю властивість ку­тів трикутника, а учні шляхом виконання практичних завдань переко­нуються у істинності цього твердження: виконуючи вимірювання кутів транспортиром на моделях і обчислюючи їхню суму вони ви­значають, що вона дорівнює 180°.

У другому випадку робота організовується в зворотному порядку: вчитель роздає трикутники, учні проводять вимірювання і додають отримані результати між собою.

Потрібно зазначити, що розумово відсталі учні під час вимірюван­ня кутів можуть допускати неточності. Тому вчителю потрібно конт­ролювати їхню роботи і у випадку необхідності надавати допомогу. При вимірюванні кутів дітьми допустима похибка - 1-2°. Враховую­чи це і в першому, і в другому випадках бажано спочатку брати три­кутники, кути яких дорівнюють круглим числам (30°, 40°, 60° і т.д.), а вже потім використовувати інші (25°, 31°, 47° і т.д.).

Закріплюючи знання цієї властивості вчитель ставить практичні завдання, виконання яких вимагає від учнів певного інтелектуального напруження: якщо величина першого і другого кутів по 90°, яка це буде геометрична фігура?; якщо один кут більше 90°, то яка буде су­ма другого і третього кутів?; якщо два кути по 45°, то яка величина буде третього кута?; якщо два кути по 60°, яка буде велична третього?

Наприкінці цього року школярі вчаться виконувати обчислення периметру трикутника. Докладніше пояснення, що таке периметр і методику його визначення у геометричних фігурах ми розкриємо при вивченні властивостей квадрата і прямокутника. Тут лише зазначимо, що проводячи пояснення вчитель вказує, що трикутник обмежують відрізки. Оскільки периметр - це сума сторін геометричної фігури, то периметр трикутника обчислюється за формулою: Р = а + Ь + с.

У 7-му класі, відповідно до програми, школярі вчаться будувати трикутник за заданою довжиною двох сторін і кута між ними. Пояс­нення цього матеріалу може даватись у двох варіантах: у першому випадку - будуємо кут заданої величини, а потім на його сторонах відкладаємо відрізки певної довжини, ставимо точки і з'єднуємо їх між собою (див рис. 9.32.)

Рисунок 9.32.

В

А С

У другому випадку спочатку на довільній прямій відкладаємо від­різок заданої довжини, потім будуємо кут вказаної величини і на його другій стороні ставимо точку відповідно до довжини другого відріз­ка. З'єднуємо її з закінченням першого відрізку. І перший, і другий варіанти доцільно пояснити розумово відсталим учням. Але при цьо­му потрібно врахувати, що вони повинні спочатку навчитись будува­ти трикутник за одним варіантом, а вже потім переходити до другого.

Рисунок 9.33.

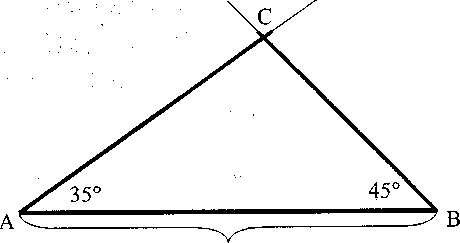
7 см

У цей же час учні вчаться будувати трикутник за однією стороною і двома суміжними з нею кутами. Пояснювати виконання цього завдання потрібно вчитель може з прикладу: необхідно побудувати трикутник, де довжина сторони АВ = 7 см, величина <А = 35°, <В = 45°. Для пояснення доцільно використати таку пам'ятку:

1. На довільній прямій відклади відрізок АВ довжиною 7 см.

2. З допомогою транспортира визнач <А = 35°, і з точки А побу­дуй кут даної величини.

3. З допомогою транспортира визнач <В = 45°, і з точки В побу­дуй кут даної величини.

4. На перетині цих ліній поставимо точку С і отримаємо АСВ (див. рис. 9.33.).

У 8-10-му класі відбувається закріплення знань про трикутники, про їхні властивості та способи побудови.