9.2. Коло і круг

З колом і кругом учні зустрічались в молодших класах, але повно­го уявлення про ці фігури у них ще немає. Тому у 5-му класі прово­диться повторення цього матеріалу. Для того, щоб школярі пригадали різницю між колом і кругом вчитель їх креслить і відповідним чином замальовує. У колі вони креслять радіус і дають йому визначення: радіус - це відрізок, який сполучає будь-яку точку кола з його центром Вони також повторюють, що коло – це крива замкнена лінія, будь яка точка якої знаходиться на однаковій відстані від центра; коло 1 це лінія, яка обмежує круг.

Основна мета, яку переслідує повторення, домогтися того щоб школяри усвідомили, що замкнена крива лінія буває різної форми, але колом ми називаємо її лише тоді, коли у ній витримуються певні вла­стивості, зокрема властива, пов'язана з радіусом (див. рис 9 21 ).

Закріплюючи знання про радіус учні вчаться позначати його від­повідною літерою латинського алфавіту: R1.

Р исунок 9.21.

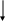
У відповідності з програмою у 6-му класі школярі вивчають новий елемент кола - діаметр. Педагог дає визначення: діаметром назива­ється пряма лінія, яка сполучає дві його точки і проходить через центр. Він пояснює, що діаметр проводиться через три точки: дві з яких лежать на колі і одна позначає його центр. При цьому повинен утворитися відрізок. Якщо пряма лінія не утворюються - це не є діа­метр.

Рисунок 9.22.

Вимірюючи два відрізки, ОА і ОВ учні пересвідчуються, що вони є радіусами, адже сполучають центр кола з точкою на колі, а лінія АВ - діаметр, оскільки вона сполучає дві точки, які лежать на колі, проходить через його центр і утворює пряму. Отже, діаметр містить у собі два радіуси. Закріплюючи знання його властивостей вчитель че­рез практичні вправи підводить дітей до усвідомлення, що в колі мо­жна провести безліч радіусів і діаметрів, що будь-який діаметр дорівнює сумі двох радіусів. Для цього відводяться практичні заняття з креслення кіл. Учні пересвідчуються, що діаметр складається з двох радіусів, і якщо стоїть завдання-накреслити два кола, одне з радіусом З см, а друге - з діаметром 6 см учень знає, що вони однакові. При ви­конанні таких завдань слід уникати симетрично розташованих діа­метрів, адже школярі звикають до цього і при виконанні завдань намагаються креслити їх лише у такому положенні.

Після розгляду діаметра учнів знайомлять з хордою. Але перед цим вчитель креслить коло і проводить через нього лінію (див. рис. 9.23.). Він формує у школярів розуміння того, що дана лінія назива­ється січною, оскільки перетинає коло у будь-якій його частині. Ця назва походить від слова "сікти", тобто вона розсікає коло на частини.

Рисунок 9.23.

с ічна

Після усвідомлення школярами поняття січної вчитель дає визна­чення: хорда - це частина січної, яка проходить в середині кола і спо­лучає дві його точки; найбільша хорда - це діаметр (див. рис. 9.24.).

Рисунок 9.24.

с ічна

хорда

У 7-му класі вчитель закріплює ці знання і пояснює деякі власти­вості хорд: чим вона далі від центру кола - тим менша її довжина; найдовша хорда не перевищує довжини діаметра кола.

Після вивчення хорди пояснюються, що таке дуга. Для того, щоб розумово відсталі краще зрозуміли це, її виділяють кольоровими олівцями. Властивості дуги вони не вивчають. Головне завдання вчителя - сформувати у них розуміння дуги і вміння показувати її на колі.

Для закріплення знань про радіус, діаметр і хорду вчитель прово­дить геометричні диктанти, на яких учні креслять кола за заданим ра­діусом, діаметром, порівнюють їх між собою, проводять у них хорди, визначають довжину діаметрів, радіусів тощо. В цей період школярі позначають радіус і діаметр латинськими буквами r(R) і d (D).

У 10-му класі відповідно до вимог нової програми вчитель знайо­мить розумово відсталих з сектором і сегментом. Цей матеріал мож­на пов'язати з дробами і діленням круга на частини. Доцільно спочатку показати частини на рисунку.

Рисунок 9.25.

А А

сектор сегмент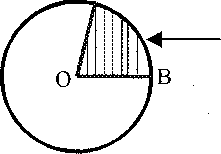

В

Потім дається визначення: сектором називається частина круга, яка обмежується дугою АВ і двома радіусами, проведеними до кінців цієї дуги; сегментом називається частина круга, обмежена хордою й дугою, яка її стягує. Для закріплення цих знань учні креслять круги різних діаметрів і вчаться виділяти у них сектор і сегмент.