9. Формування знань про властивості геометричних фігур та тіл в учнів старших класів допоміжної школи

9.1. Кути

3.5-го по 10-й клас на вивчення геометричного матеріалу підво­диться за програмою щотижня по одній годині. До цього часу школя­рі вже отримали систему елементарних знань про геометричні фігури: знають їхні назви, впізнають серед інших, мають навички їх­нього креслення, володіють знаннями про їхні властивості.

Більшість учнів після закінчення допоміжної школи закінчують навчання і йдуть працювати на виробництво. Тому вони повинні мати закінчену систему уявлень і понять про геометричні фігури. Врахо­вуючи це дітям потрібно дати систему геометричних з'явлень.

У старших класах повторення матеріалу про геометричні фігури складається з вправ на впізнання їх за образом, за вибірковою назвою, відтворення їх назв і образів, основних властивостей тощо. Без вправ на повторення не можна переходити до знайомства з геоме­тричними формами.

Починають школярі вивчення геометричного матеріалу з повто­рення властивостей точки, лінії та кута. У цей час вони пригадують креслення прямих, ламаних, кривих ліній, відрізка у різних напрям­ках, визначають їхні властивості, виконують вимірювання за допомо­гою лінійки, повторюють послідовність користування циркулем та косинцем. Відповідно до вимог програми знайомляться з позначен­ням геометричних фігур літерами. Вони позначають ними відрізки, кути, сторони фігур. Введення цієї символіки не лише допомагає роз­різняти фігури і їхні елементи, але є одним із засобів формування узагальнень і порівнянь, розвитку абстрактно-логічного мислення.

У 5-му класі учні удосконалюють свої вміння знаходити відрізок, пряму, криву, ламану лінії на рисунках. Вони визначають довжину ламаної шляхом додавання довжин відрізків, які її утворюють.

У відповідності до "Програми для допоміжної школи: Математика. 5-10 клас"^* у 1 -й та 2-й чверті 6-го класу вводиться поняття "гори­зонтальна", "вертикальна" та "похила" пряма. На теперішній час на Україні не надруковані нові підручники з математики для допоміжної школи. Оскільки даний матеріал розміщений у підручнику з матема­тики для 5-го класу^** педагогу потрібно враховувати це у навчально­му процесі. Такі невідповідності розміщення матеріалу у "Програмі..." та підручниках з математики будуть зустрічатись і на­далі.

Почати вивчення цих властивостей прямої лінії доцільно з форму­вання поняття про горизонталь. Для цього краще всього показати школярам лінію горизонту. Потім вчитель креслить лінію і називає її: горизонтальна. Організовуючи роботу над цим матеріалом він знайо­мить учнів з рівнем, з допомогою якого вони зможуть визначати го­ризонтальне положення ліній, плоских предметів, планок тощо. Педагог пояснює, що рівень - це прилад для перевірки горизонталь­ності ліній. Він розповідає, що рівнем користуються на будівництві для контролю горизонтальних частин будинків. Найчастіше рівень -це дерев'яний брусок з вкладеною в нього скляною трубкою, на якій нанесені мітки. Скляна трубка дещо вигнута посередині для того, щоб можна було чіткіше визначити горизонтальність тієї чи іншої поверхні. На уроці школярі повинні потримати його в руках і потре­нуватись у його використанні.

Після цього учнів знайомлять з вертикальною лінією. Для цього педагог використовує визначення: лінія, яка проходить під прямим кутом до горизонтальної, називається вертикальною. Він показує школярам вертикальні лінії: дерева, телефонні стовпи, стіни будинків тощо. Під час проведення практичних занять на закріплення даного поняття діти знайомляться з новим приладом - виском, за допомогою якого визначають вертикальні прямі. На практичному занятті школя­рі зможуть його виготовити самостійно. Далі він розповідає, що цей прилад знову ж таки використовують на будівництві для перевірки вертикальності стін, ніш для дверей, вікон тощо.

Познайомившись з горизонтальними та вертикальними лініями педагог може навести приклад похилої лінії, нарисувавши її на дошці поряд з ними. При цьому він рисує декілька похилих ліній, які розмі­щуються під різним кутом до горизонту. Педагог робить це тому, що формує у розумово відсталих учнів усвідомлення, що будь-які лінії, які не є вертикальними або горизонтальними називаються похилими. Для закріплення цих знань організовується лабораторно-практичне заняття, на якому школярі рисують лінії у різних напрямках і підпи­сують під ними відповідні назви (див. рис. 9.1.). Такі вправи доцільно виконати на уроках не лише вивчення геометричного матеріалу, але й математики і відвести на них 5-7 хвилин.

Р исунок 9.1.

Вертикальна лінія Горизонтальна лінія Похилі лінії

Вчитель після цього пояснює такі властивості ліній, як паралель­ність і перпендикулярність. Починається все з вивчення визначення: лінії, які лежать на одній площині і ніде не перетинаються, скільки б ми їх не продовжували, називаються паралельними. Потім він наво­дить приклад паралельних і непаралельних ліній, креслячи їх на дош­ці (див.рис.9.2.).

Рисунок 9.2.

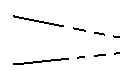
Паралельні ліній Не паралельні лінії

Він розповідає, що будувати паралельні лінії можна за допомогою лінійки і косинця і пояснює, що паралельність прямих позначається знаком "Ц", наприклад: АВ ||МК. Відстань між паралельними прями­ми визначається по перпендикуляру, який опускають з точки однієї прямої на іншу під прямим кутом. Причому учні переконуються, що відстань між паралельними прямими завжди однакова. Якщо вона збільшується або зменшується - прямі перетнуться і, отже, вони не є паралельними. Школярі також повинні познайомитись з тим, що па­ралельних прямих буває декілька, причому відстань між різними па­рами не завжди однакова.

Р исунок 9.3.

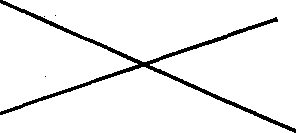
Перпендикулярні лінії Не перпендикулярні лінії

Після цього вони переходять до вивчення перпендикулярності. Так само, як і при паралельності, вивчення цього матеріалу почина­ється з визначення: якщо при перетині двох ліній утворюється прямий кут, такі лінії називаються перпендикулярними. Перпендикулярність позначається знаком "┴", наприклад: СО┴ВЕ. Далі він наводить приклад перпендикулярних і не перпендикулярних ліній (див. рис. 9.З.).

У 5-му класі вчитель декілька уроків відводить на знайомство з ді­аграмою. Для цього він пропонує учням зробити скорочений запис задачі і розв'язати її. Наприклад: "До шкільної їдальні привезли 8 мі­шків. У 5 з них була з гречка, у решті - рис. Скільки було мішків із рисом?" Педагог пропонує учням зобразити це наочно. Школярі, як правило, можуть знайти її розв'язок за допомогою арифметичних дій. Але завдання педагога в тому, щоб навчити їх складати діаграми. Тому він пропонує накреслити відрізок, умовно взявши позначення: 1 см = 1 мішок. Оскільки учні знають, скільки всього мішків привез­ли, вони креслять відрізок довжиною 8 см. Після цього потрібно від­мітити на ньому 5 мішків із гречкою і полічити ті сантиметри (мішки), які залишились (див. рис. 9.4.).

Рисунок 9.4.

гречка рис

Розв'язавши задачу таким чином вчитель пояснює, що частіше всього для позначення використовують не відрізки, а стовпчики, по­дібні до прямокутників. їх ширина може бути різна, головне - доби­тись правильних пропорцій висоти. Діаграма - це креслення, яке наочно зображує пропорції між різними величинами.

У цей період школярі закріплюють знання про основні властивос­ті кутів, їхні типи, вміння їх креслити. Вчитель організовує практичні заняття з виділення прямих, тупих і гострих кутів. Оскільки знання з геометрії мають бути максимально пристосовані до життя в соціаль­ному середовищі вчитель вводить таке поняття, як кутник. Він розповідає про його властивості і використання у слюсарній та столярній справі. Бажано показати різні кутники, які є у майстерні.

У відповідності з новою програмою в 7-му класі педагог на моде­лях кутів, сторони яких з'єднані шарнірно, знайомить учнів із розгор­нутим кутом. Для цього він використовує два прямі кути, сторони яких з'єднані шарнірно: два прямих утворюють один розгорнутий (див. рис. 9.5.). Закріплення проводиться на практичних заняттях, на яких він пояснює, для чого потрібно вміти будувати розгорнуті кути, пов'язуючи матеріал з уроками трудового навчання.

Рисунок 9.5.

прямий кут

розгорнутий кут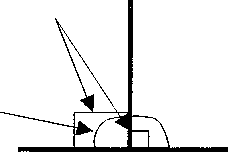

Після усвідомлення розгорнутого кута і його побудови дітей зна­йомлять з повним кутом, який складається з чотирьох прямих. Для пояснення використовуються дві прямі, які перетинаються під пря­мим кутом. На такому рисунку легше показати і розгорнутий, і повний кут.

Продовжуючи закріплення знань про відрізок і його властивості вчитель пояснює, як можна виконати поділ відрізка на дві рівні час­тини за допомогою циркуля. Перед цим він проводить пояснення, що в деяких випадках для креслення геометричних фігур потрібно знай­ти середину відрізка, причому довжина може бути наді невідома. То­му для виконання цього завдання використовують його поділ за допомогою циркуля і наводить зразок виконання цього завдання (див. рис. 9.6.).

Р исунок 9.6.

а b

Відрізок a дорівнює відрізку b.

У 6-му класі розумово відсталих учнів знайомлять з таким понят­тям, як масштаб (на сучасному етапі деякі педагоги використовують термін "мірило"). Для пояснення цього матеріалу створюється про­блемна ситуація: "З одного населеного пункту в інший вийшов хлоп­чик, який рухався зі швидкістю 4 км/год. З іншого населеного пункт}/ в напрямку першого, через 30 хв вийшла дівчинка, яка рухалась зі швидкістю 3 км/год. Яку відстань подолає кожен із них до зустрічі, якщо відстань між населеними пунктами 16 км?" Вчитель ставить перед учнями завдання: розв'язати задачу, зробивши її графічний за­пис. Більшість школярів не знає, як правильно виконати це завдання. Тоді педагог повідомляє, що коли в задачі йде мова про кілометри або про інші великі міри довжини, які ми не можемо накреслити у зо­шиті, можна вдатись до використання такої умовної міри, як масштаб.

Вчитель дає визначення: масштаб - це співвідношення довжини лінії, накресленої в зошиті (на кресленні, карті, плані) до зображува­ної нею дійсної довжини. Масштаб показує, у скільки разів відстань на місцевості зменшено для її відображення на карті або плані. Він використовується для зображення на карті чи плані значних відста­ней і з його допомогою можна показати великі відстані у зменшено­му вигляді. Чим більші відстані на карті, які потрібно зобразити – тим дрібніший потрібно брати масштаб. Масштаб може бути вказа­ний числом (так званий числовий масштаб), або прямолінійним відрізком (так званий лінійний масштаб). В останньому випадку такий відрізок бути ділитися на частини з цифрами, які вказують на дійсну його довжину.

Зробивши таке пояснення вчитель виконує графічний запис даної задачі з використанням лінійного масштабу.

Рисунок 9.7.

А 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16В

30 хв 1 год 1 год 1 год 1 год

хлопчик дівчинка

Такий запис дозволить розумово відсталим учням зрозуміти, що таке масштаб і для чого він використовується. Після цього пропонує учням розглянути різні карти і звернути увагу на те місце, де позначе­но масштаб. Він пояснює, що запис, наприклад, 1:10000 означає, що в 1 см карти відображено 1000 метрів на місцевості.

Цей матеріал закріплюється на уроках географії, природознавства, трудового навчання.

Після проведення такої роботи школярі повинні самостійно роз­шифровувати карти і співвідносити масштаб, який у них показується з дійсними мірами довжини. Протягом всього періоду навчання вчи­тель постійно повертається до роботи по визначенню масштаба.

На уроках геометрії у 6-му класі учні виконують арифметичні дії з відрізками. Почати потрібно з дій додавання й віднімання. Вчитель пояснює, що відрізки мають певну довжину з ними можна виконува­ти відповідні арифметичні дії. Наприклад, дано два відрізки а і Ь:

А В= 4 см 7 мм

А а В

В С= 7 см 8 мм

В b С

Для того, щоб знайти їхню загальну довжину потрібно об'єднати їх.

А В С

Отже, АВ + ВС = АС, оскільки АВ = 4 см 7 мм, а ВС = 7 см 8 мм, то АС = 4 см 7 мм + 7 см 8 мм = 12 см 5 мм.

Для закріплених цих знань вчитель організовує практичні вправи, при виконанні яких школярі переконуються у правильності обчис­лень через вимірювання утворених відрізків. Аналогічно проводить­ся пояснення знаходження різниці відрізків.

Після цього вчитель пояснює методику звільнення відрізків у 2, З, 4 рази. Для цього він повертається до визначення: множення - це до­давання однакових доданків. Отже, збільшити відрізок у 2 рази озна­чає до даної величини відрізка додати ще таку саму величину. Також в цей час в учнів формується вміння ділити відрізки на дві рівні час­тини. Оскільки вони вже вміють ділити відрізок на дві рівні частини за допомогою циркуля, ці знання стають їм у нагоді: після обчислен­ня довжини відрізка арифметичною дією ділення школярі виконують практичний поділ, вимірюють відрізки і переконуються у правильно­сті результату.

В 7-му класі учнів знайомлять з бісектрисою кута. Вчитель дає ви­значення: бісектриса кута - це промінь, який виходить із вершини ку­та і ділить його на дві рівні частини. Таке визначення він закріплює виконанням практичних вправ. Спочатку школярі вирізають накрес­лений кут і перегинають його пополам. Педагог вказує, що лінія, яка утворилась, ділить його на дві рівні (або симетричні) частини. Це і є бісектриса кута.

Після того, як вони зрозуміли, що таке бісектриса, доцільно орга­нізувати роботу з її побудови за допомогою циркуля і лінійки. Для Цього можна використати пам'ятку приблизно такого плану:

1. Накресли кут.

2. Постав ніжку циркуля у вершину кута і на його сторонах дові­льним розхилом зроби дві помітки.

3. З'єднай ці точки лінією.

4. Постав ніжку циркуля у точку, яку ти позначив на бічній сторо­ні і розхилом циркуля, більшим за половину цієї лінії в середині кута проведи півколо.

5. Постав ніжку циркуля у точку, яку позначив на другій його сто­роні і не змінюючи розхилу в середині кута проведи друге півколо.

Накресли лінію від вершини кута через точки, які утворились від перетину двох півкіл. Це і є бісектриса кута (див. рис. 9.8.).

Рисунок 9.8.

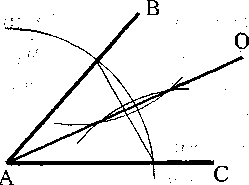
Можна запропонувати учням вирізати рисунок і перевірити шля­хом перегинання, чи справді ця лінія ділить цей кут пополам.

Після того, як школярі навчаться використовувати градуси для креслення кутів, доцільно накреслити бісектрису з використанням такої пам'ятки і запропонувати їм виміряти транспортиром кути, які при цьому 5'творились. Це дозволить їм пересвідчитись, що викорис­товуючи транспортир або запропоновану нижче пам'ятку можна по­ділити кут на дві рівні частини.

Програмою з математики передбачено знайомство школярів з віс­сю симетрії, її центром та симетричними фігурами. Спочатку вчитель показує школярам симетрично розташовані фігури. Для цього він ви­користовує такі рисунки фігур, де ліва і права сторони однакові. Про водячи їх перегинання вчитель показує, що його дві половинки симетрично розташовані відносно тієї лінії, яка утворилась при пере­гинанні. Він просить школярів докладно роздивитись дві половинки і зробити свої висновки: права і ліва сторони однакові. Після цього мо­жна запропонувати школярам серед різних рисунків вибрати ті, які після перегинання утворять симетричні половинки.

Вивчення вісі симетрії починається з визначення: будь-які дві точ­ки будуть симетричними відносно точки О, якщо точка О - середина відрізка, якого вони утворюють. В такому випадку точка О називаєть­ся віссю симетрії. Для підкріплення теоретичних знань вчитель крес­лить пряму і позначає на ній точки на однаковій відстані відносно центру.

● ● ●

А О А1

В ін пояснює: "Оскільки відрізок ОА дорівнює відрізку ОА1, точки А і А1 симетричні відносно точки О. Отже, дві точки (А і А1), які ле­жать на одній прямій з третьою (О) і віддалені від неї на однакову від­стань, називаються симетричними". Для закріплення цих знань він розповідає, як позначити на прямій точку, симетричну даній відносно центру симетрії О за допомогою циркуля.

● ● ●

А О А1

Після цього доцільно організувати достатню кількість тренуваль­них вправ на уроках з вивчення геометричного матеріалу, відводячи для цього 15-20 хвилин уроку залежно від пізнавальних здібностей розумово відсталих.

Проводячи пояснення послідовності побудови кола вчитель почи­нає з визначення точку, яка є симетрична відносно центра даного ко­ла. Оскільки з цим матеріалом школярі вже знайомі, то побудувати Цю точку вони зможуть самостійно. Вчителю залишається лише по­яснити, що ця точка - це центр кола і якщо ми його накреслим, то отримаємо коло О1, симетричне коло О відносно осі симетрії (див. рис. 9.9.).

Рисунок 9.9

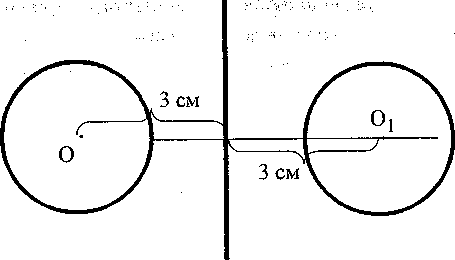
Для закріплення знань вчитель вирізує круг і перегнувши його по­полам підводить учнів до висновку, що його половинки однакові. При цьому він звертає увагу, що лінія, яка при цьому утворилась, є його діаметром. Отже, діаметр круга є віссю його симетрії.

Сформувавши вміння будувати коло відносно центра симетрії вчитель аналізує інші фігури. Учні переконуються, що у рівностороннього трикутника є три осі симетрії, у рівнобедреного - одна. В де­яких трикутниках взагалі немає осі симетрії, адже вони не діляться на дві рівні частини. Така сама робота виконується з прямокутником й квадратом.

Після розгляду симетричних фігур переходять до вивчення симет­рично розташованих предметів. Для цього вчитель організовує спо­стереження і аналіз рисунків, на яких є такі зображення, виділяє симетричні предмети у класі, в інших шкільних приміщеннях.

Головною темою 7-го класу є вимірювання кутів та їх креслення за допомогою транспортира. Вивчення градусної міри вимагає ґрунто­вного повторення знань про кути, їхню побудову та властивості. При вивченні цієї теми розумово відсталі учні часто допускають грубі по­милки. Головна проблема, яка стає на шляху усвідомлення ними цьо­го матеріалу полягає не лише в тому, що поняття "кут" вимагає високого розвитку логічного мислення, але й в тому, що вони почина­ють використовувати вимірювальну шкалу, яка розміщується не на прямій, а по дузі. На транспортирі 0 може лежати і з ліва, і з права, шкала двобічна, "мітка" може міститись у різних місцях на основі. Це вносить дисбаланс у роботу мислення розумово відсталих.

За допомогою транспортира учнів допоміжної школи вчать розв'я­зувати такі завдання: 1) дано кут - виміряти його величину; 2) дано величину кута - побудувати його.

Якщо з першим завданням вони справляються легко, то в процесі роботи над другим у них зустрічаються певні труднощі. Отже, почи­нати навчання доцільно з формування вміння вимірювати величину кута з допомогою транспортира, тобто просуватися від легкого до складного.

Вчитель починає з розповіді, що для вимірювання кутів існує спе­ціальний прилад, який називається транспортир. Він являє собою мо­дель розгорнутого кута, поділеного на градуси. Відлічувати градуси можна з обох кінців транспортиру і тому кожні 10° позначаються на ньому двома цифрами: 10° і 170°; 20° і 160°; 80° і 100°. У центрі транспортира є риска, яку потрібно суміщати з вершиною кута. Далі починається практична робота з формування вміння суміщати центр транспортира з вершиною кута. Для цього він пояснює, що вимірю­вання кута за допомогою транспортира починається не з кінця ліній­ки, а з нульової позначки на транспортирі, яка стоїть на середині його основи. Потім розповідає, що лінійка транспортира ставиться з однієї сторони кута так, щоб його вершина співпала з центром транспорти­ра. Друга сторона має пересікати дугу транспортира в певній точці. Ця точка і вказує на величину кута. Якщо точку поставили на відміт­ці шкали транспортира, наприклад, 65°, отже, величина кута 65°.

Для закріплення навичок вимірювання кутів потрібно організува­ти достатню кількість вправ. Спочатку доцільно вчити школярів ви­мірювати кути з величиною 20°, 30°, 50°, 90°. Потім перейти до вимірювання кутів в 87°, 29°, на останньому етапі - 112°, 157°, 180°. Головне при організації цієї роботи - домогтися того, щоб вони на­вчились правильно зіставляти транспортир із кутом, який потрібно виміряти. Під час діяльності вчитель вимагає називати тип кута, який вони виміряли: прямий, тупий чи гострий. Для цього він робить за­пис, що кути від 0° до 89° - гострі, 90° - прямий кут, від 91 ° до 179° -тупі.

Після цього пояснює креслення кута заданої величини за допомо­гою транспортира. У допоміжній школі використовується два варіан­ти пояснення цього матеріалу.

При використанні першого варіанту учнів вчать ставити три точ­ки: центр транспортира, нульову позначку на його лінійці й позначку на його дузі. Останню точку вони знаходять таким чином: рахують від нуля по 10 до відповідного градуса, наприклад, 60°. Після цього з'єднують точку, яка вказує на його вершину з двома іншими й отри­мують кут відповідної величини.

При використанні другого варіанта можна використати пам'ятку:

1. Накресли промінь з початком в точці О. Це - вершина кута.

2. Сумістити центр транспортира з точкою О.

3. По градусній дузі знайти відмітку 60°, починаючи від нульової позначки і поставити точку А.

4. Забравши транспортир з'єднати з допомогою лінійки утворену точку з точкою О (див. рис. 9.10.). Утворився кут АОВ величиною 60°.

Рисунок 9.10.

А

О В

Якщо школярі забудуть, по якій дузі транспортира вони проводять відлік градусів, може бути допущена помилка: замість гострого кута накреслять тупий. Тому для попередження цього після визначення точки по дузі транспортира від учнів потрібно вимагати назвати кут, який при цьому отримали: прямий, тупий, гострий чи розгорнутий. Закріплюючи цей матеріал школярі вимірюють кути у трикутни­ків, прямокутників, багатокутників, будують їх за заданими розміра­ми, вказують їхню величину тощо.

У цей період вони знайомляться з властивостями суміжних кутів. Вчитель дає визначення: суміжними називаються кути, у яких одна сторона спільна, а дві інші утворюють пряму. Школярам потрібно по­яснити головну властивість суміжних кутів: щоб побудувати кут, су­міжний з даним, треба одну з сторін даного кута продовжити за його вершину (див. рис. 9.11.).

Рисунок 9.11.

М

О А В

Учні повинні усвідомити і таку закономірність: якщо відома гра­дусна міра одного суміжного кута, можна взнати величину другого кута шляхом віднімання від 180° відомої величини першого кута, адже їхня спільна величина - 180°. Наприклад, <ВАМ=35° (див. рис. 10.11.). Для того, щоб визначити величину <ОАМ потрібно від розгорнутого <ОАВ відняти величину <МАВ. Отже, <ОАМ = <ОАВ - <МАВ = 180° - 35° = 145°.

Потрібно зазначити, що розумово відсталим важко усвідомити властивості суміжних кутів, тому вимагати знання цього матеріалу від усіх учнів недоцільно. З кращими школярами в 9-10-му класах можна розглянути суміжні кути, які утворюються при перетині двох прямих ліній. Під час пояснення можна дати визначення вертикаль­них кутів і довести рівність протилежних кутів, які утворюються при перетині двох прямих. Для цього спочатку виконується креслення (див. рис. 9.12.)

Рисунок 9.12

Потім проводимо порівняння суміжних кутів:

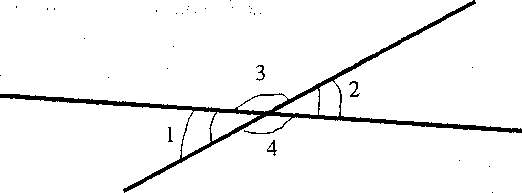
1)<1 + <3 = 180° <2+<3 = 180°

Оскільки <3 = <3,то <1 = <2

2)<3 + <2 = 180°

<4+<2=180°

Оскільки <2=<2, то <3=<4

Починаючи з 8-го класу школярі вчаться будувати фігури, симет­ричні відносно осі симетрії. Для цього вчитель показує вже готові зразки симетрично накреслених фігур. Він пояснює, що точки будь-якої фігури, яку будують відносно осі симетрії, повинні знаходитись на однаковій відстані від неї. Вони вивчають правило: дві фігури на­зиваються симетричними, якщо кожній точці однієї фігури відпові­дає така ж точка іншої, рівновіддалена від осі симетрії. При цьому потрібно зазначити, що будь-які фігури, симетричні відносно осі, рів­ні між собою.

Засвоєння властивостей симетричності дозволяє педагогу разом з учнями переходити до побудови симетричних фігур. Робота почина­ється з того, що школярі креслять відрізок і позначають на ньому лі­терами його кінці: АВ. Відрізок бажано креслити похило. Після цього вони проводять вертикальну пряму і позначають її відповідно КМ. З кінців відрізка АВ проводять дві горизонтальні прямі, які при перетині з прямою КМ утворюють прямі кути. Точки перетину потрі­бно позначити відповідно О і О1. Вони є точками симетрії. Після цього учні беруть циркуль і відкладають на цих горизонтальних прямих дві точки: А1 і В1. Сполучивши їх отримують відрізок А1В1, симет­ричний відносно прямої КМ відрізку АВ (див. рис.9.13.).

Рисунок 9.13.

К

А О А1

О1

В М В1

Рисунок 9.14.

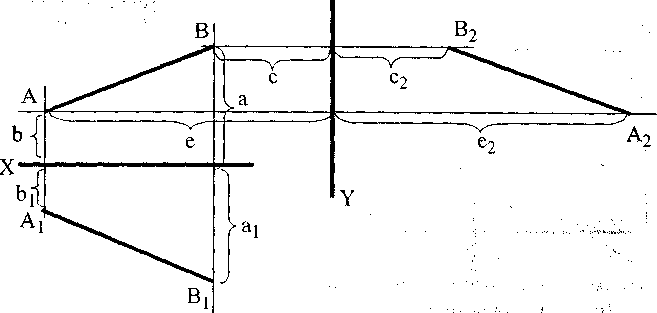
В наступних класах вчитель повертається до даного матеріалу, закріплюючи й удосконалюючи знання школярів. Поступово він пере­ходить до креслення двох симетричних відрізків відносно даного через дві осі симетрії, які проведені у різних напрямках. При цьому дається пояснення, що для будь-якого відрізка (а наділі і фігури) мож­на побудувати відрізок (фігуру) симетричний до нього відносно будь-якої осі симетрії. На рисунку видно, що відрізку АВ можна побудува­ти два симетричних: відрізок А1 В1 відносно осі X і відрізок А2 В2 від­носно осі Y. (див. рис. 9.14.).

У 8-му класі школярі креслять геометричні фігури, симетричні відносно осі. Педагог пояснює: щоб побудувати трикутник, симетри­чний даному, потрібно побудувати точки, симетричні його вершинам стосовно осі симетрії, а потім сполучити їх між собою. На перших етапах роботи доцільно підбирати фігури, при побудові симетричних яким точки не є на одній прямій. Це потрібно тому, що розумово від­сталі школярі спочатку не усвідомлюють, що на одній прямій, яку ми проводимо для утворення симетричної фігури, може розміщуватись одразу дві симетричні точки. Наводимо приклад правильного і непра­вильного підбору геометричних фігур для пояснення на уроках (див. рис. 9.15.).

Рисунок 9.15.

В В1

А А1

С С1

(неправильний підбір фігур) (правильний підбір фігур)

Вивчаючи тему "Кути" не можна обмежуватись лише роботою в класі. Слід навчити учнів будувати їх на місцевості. Для його вчитель може організувати роботу з екером.

Екер (від фр. equerre - зробити, виконати і quadrare - чотирикут­ний) - це топографічний інструмент, що служить для відкладання на місцевості кутів певної величини (здебільшого 90°, 60° або 45°).

С.М.Попович зазначає, що у допоміжній школі за допомогою еке­ра можна вирішити два завдання^*:

1. Побудувати прямий кут, якщо напряму жодної із сторін не задано (див. рис. 9.16.)

2. Побудувати прямий кут, якщо задано напрям однієї з його сто­рін (див. рис. 9.17.)

Рисунок 9.17.

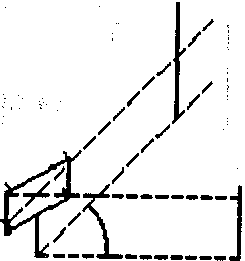
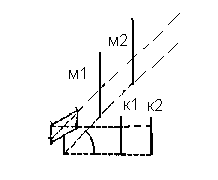
Для побудови прямого кута з довільним напрямом сторін потрібні дві віхи, а для вирішення другого завдання - чотири.

У 10-му класі вчитель закріплює уявлення про різні варіанти діа­грам: лінійні, стовпчикові, кругові. У цей період школярі вчаться креслити кругові діаграми. Працюючи над формуванням вміння їх будувати, вчителю спочатку потрібно нагадати, що таке діаграма і коли вона використовується. Після цього він пояснює, що їхня назва пов'язана зі словом "круг". Круговими діаграмами ми можемо позна­чати співвідношення між різними частинами. Наприклад, дається задача: "У фермерському господарстві було 300 га ріллі. 25% ріллі засіяли горохом, 50% - пшеницею, 15% - житом, решту - рапсом. Скільки ріллі засіяли рапсом?" Для розв'язання цієї задачі можна скласти кругову діаграму (див. рис. 9.18). Використання такої діа­грами допомагає школярам наочно пересвідчитись, що житом засія­ли найменше ріллі.

горох жито пшениця рапс

Рисунок 9.18.

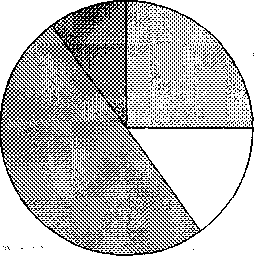
Рисунок 9.19.

Завод Фабрика

Аналогічно даються пояснення властивостей та побудови стовпчикових та лінійних діаграм (див. рис. 9.19 і 9.20.).

Рисунок 9.20.

1 бригада 2 бригада