43. Взаимно однозначные соответствия

Из всевозможны х соответствий, которые можно установить

между элементами двух множеств X и У, нас будут в первую

очередь интересовать такие, при которых каж дому элементу мно

жества X соответствует единственный элемент множеств а Y, и к а ж

дый элемент м ножества У соответствует только одному элементу

из множест ва X. Такие соответствия называ ют взаимно одно

значными.

Рассмотрим примеры таких соответствий.

1. Пусть Л = { а, Ь, с, d), В = {1, 2, 3, 4). Соответствие между

элементами этих множест в установлено при помощи граф а (рис. 84).

Так как каждому элементу множества А (из каж дой точки, изо

бр аж аю щей элементы множест ва А, выходит стрел ка) соответствует

единственное число из м ножества В (а -»-1, b -*■ 2, с-*-3, d 4)

и каж дое число м ножества В соответствует только одному элемен

ту множества А, то данное соответствие м ежду множест вами А и В

взаимно однозначное.

2. Пусть X — множество точек координатной прямой, a Y = R .

Так как с введением координат на прямой каждой точке сопостав

ляется единственное число (координата этой точки) и к аж дое

действительное число сопоставляется единственной точке этой

прямой (имеющей это число своей координатой), то установленное

соответствие взаи мно однозначное.

3. Пусть X — множество точек координатной плоскости, а У —

множество пар действительных чисел. Если каждой точке плоскости

сопоста вляется единственная пара действительных чисел (коорди

наты этой точки) и к аж дая пара действительных чисел сопостав

ляется единственной точке этой плоскости (имеющей эту пару чисел

своими коорди натами), то соответствие между множествами точек

координатной плоскости и множеством пар действительных чисел

взаимно однозначное.

Понятие взаи мно однозначного соот

ветствия в начально м курсе математики

используется неявно; на нем основан А

процесс счета и сравнение чисел. Так,

чтобы объяснить запис ь 3 = 3, берут три

красных квадрат а и три зеленых и к аж

дому красному к вадр ату ст авят в соот

ветствие единственный зеленый (на прак

тике квадраты прик ладывают друг к

другу, наклады вают, соединяют отр ез

ками и т. д.), т. е. устанавлива ют вза

имно однозначное соответствие между

119

этими множествами квадратов. Чтобы показать, что 3 < 4 , уста нав

ливают взаимно однозначное соответствие м ежду множеством, в

котором три элемента, и трехэлементным подмножеством множества,

сод ержащ его четыре элемента.

Упражнения

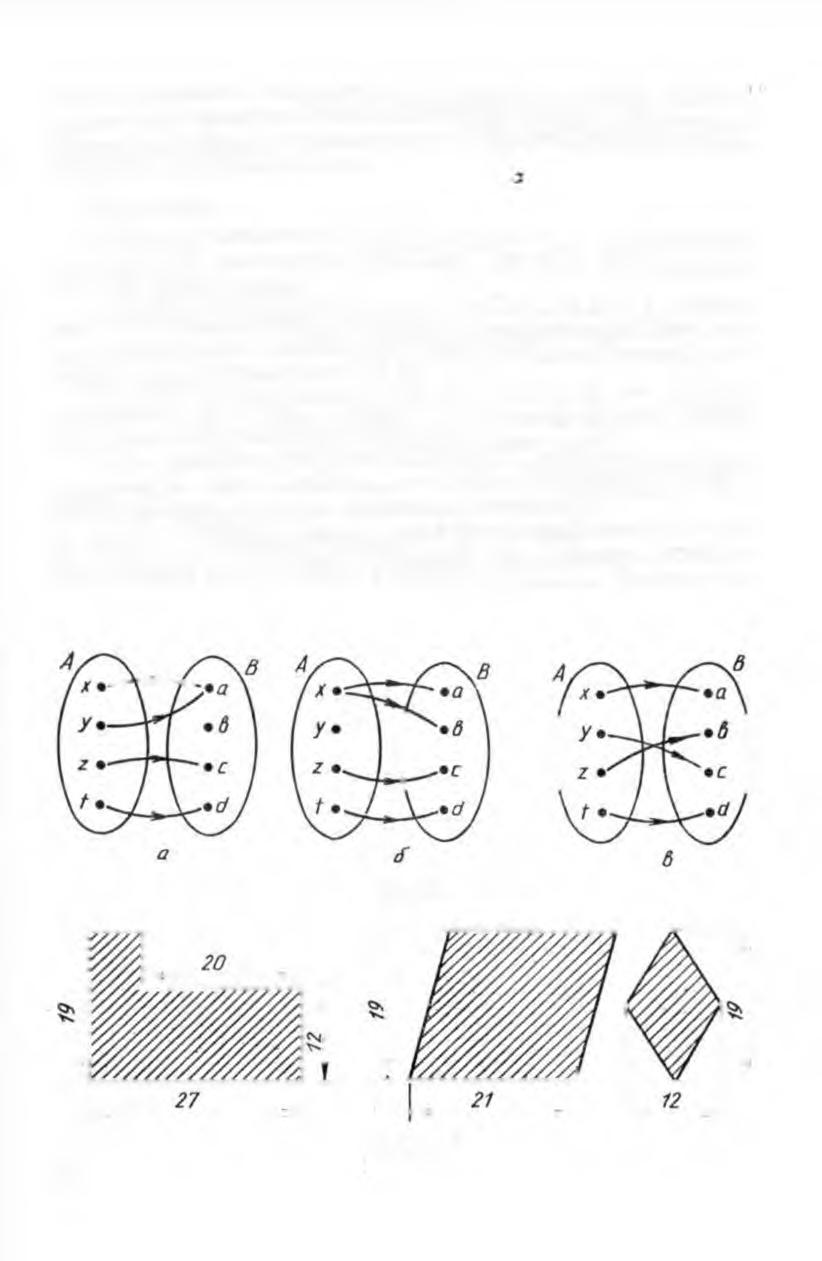
1. М еж ду множествами А = [х, у, z , /) и В = {а, Ь, с, d\ установле

ны различные соответствия (рис. 85). Какие из них явл яются

взаи мно однозначными?

2. Даны множества X = [k, I, т, п, р) и У= {1, 2, 3, 4, 5). Устано

вите три различных взаимно однозначных соответствия между дан

ными множествами. Сколько всего таких соответствий можно уста

новить между мн ожествами X и Y?

3. Д аны два множества Л = { 1, 2, 5} и В = {3, 7). Найдите

м ножества А Х В и В Х А . Можно ли каким-либо обр азом устано

вить взаимно однозначное соответствие между ними?

4. N — множество натуральных чисел, Y — множество квадратов

натуральны х чисел. Покаж ите, что между множествами N н Y

можно установить взаимно однозначное соответствие.

5. М — множество геометрических фигур, изобр ажен ных на ри

сунке 86, R — множество действительных чисел. Поставим в соответ

ствие каждой фигуре число — значен ие ее площади. Будет ли это

Рис. 85

Рис. 86

120

соо тв етст вие в заим но од нознач ным соот ветст вием м ежду м ножест

вами М и / ? ?

6.

Приведите пример ы за дан ий из учебников математики дл я

начальных классов, при выполнении которых неявно использ уется

понятие взаимно однозначного соответствия между множествами.