41. Понятие соответствия

Кроме отношений на множестве, часто приходится расс матривать

отношения между элементами двух множеств. Такие отношения н а

зыва ют соответствиями. Например, в процессе измерения длин от

резков устана вливается соответствие между отрезками и дейст ви

тельными числами; с помощью координатной плоскости устанавли

ва ется соответствие между точками плоскости и па рами дейс тви

тельных чисел.

По своей сути соответствие между элементами двух множеств

X и Y, так же как и отношение на множестве, представляет

собой множество пар и является подмножеством декартова про

изведения множеств X и У.

Соответствия м ежду конечными м ножествами наглядно пред

ставляются при помощи графов. Построим, например, г раф соотв ет

ствия «больше» м ежду элементами множеств Х = {3, 5, 7, 9) и

t il

Рис. 70

У= {4, 6}. Д л я этого обозначим элементы

данных множеств точками и проведем

стрелки от точек, и зоб ражаю щих элемен

ты множества X, к.точкам, изображающим

элементы множества У, при этом должно

выполняться соответствие «больше». Так,

стрелка должна идти от точки 5 к точке

4, поскольку 5 больше 4; должны быть

стрелки, идущие от точки 7 к точкам 4 и 6,

и т. д. В резул ьтате получаем граф

соответствия «больше» между элемента

ми множеств X и Y (рис. 70).

Соответствия между элементами числовых множеств А' и Y пред

ставл яют при помощи г рафика на координатной плоскости. Для

этого изображают все пары чисел, находящихся в соответствии R,

точками на координатной плоскости. Пол учивш аяся при этом

фигура и будет графиком соответствия R. Обратно: любое под

множество точек координатной плоскости считают графиком неко

торого соответствия.

Построим, например, график соответствия «больше» между эле

ментами множеств Л"= {3, 5. 7, 9) и К= {4, 6}. Запише м пары

чисел, на ходящихся в за дан ном отношении: (5, 4), (7, 4),

(7, 6), (9, 4), (9, 6). Изо бра зив элементы м ножества X на оси Ох,

элементы мн ожества Y на оси Оу, а каждую из получившихся

пар точкой на координатной плоскости, получим график соответ

ствия «больше» между элементами множеств X и У (рис. 71).

Такое представление соответствия позволяет на глядно изобра

жать их в тех ситуациях, когда в заданном соответствии находится

бесконечное множество пар чисел.

Рассмотрим, например, соответствие «больше» м ежду элемента

ми множеств X = R и У= {4, 6} и построим его график.

В данном слу чае элементы множества X сплошь заполняют

ось абсцисс, а множество Y состоит из двух элемен тов: 4 и 6.

Так как для элементов множест в X и Y задан о отношение «больше»,

установим, какие числа из множества X больше числа 4.

112

Рис. 71

Рис. 72

Все числа, большие 4, ра сп ол а

гаются на оси Ох вправо от точ

ки, изображающей число 4. Значит,

все точки, дл я которых абсцисса

выбирается из пр омежутка (4, оо),

а ордината равна 4, образуют луч

А В (рис. 72). Этот луч не имеет на

чала, поскольку точка (4,4) графику

данного соответствия не пр инадле

жит. Аналогично все точки, для ко

торых абсцисса выби рается из про

меж утка (6, о о ), а ордината равна 6,

образуют луч CD.

Таким образом, графиком соот

Рис. 73

ветствия «больше» между м ножествами X = R и Y — [4, G) явл яю тся

лучи А В и CD, исключая точки А и С.

Заметим, что графики одного и того же соответствия «больше»

для разных множеств различны. Чтобы еще раз убедиться в этом,

построим график соответствия «больше» (х > у ), задан ного на мно

жестве R действительных чисел, т. е. в случае, когда X = Y — R.

Все числа, у которых абсцисса равн а орди нате.ра спола гаются

на биссектрисе 1-го и 3-го координатных углов (на рис. 73 она

по каза на штриховой линией). Все точки, у которых абсцисса больше

ординаты, располага ются под биссектрисой. Чтобы убедиться в

этом, достаточно взять точку из этой области, например точку А (3, 0).

Таким образом , графиком соответствия «больше», за данного на

множестве R действительных чисел, яв ляется полуплоскость, расп о

ложенная под биссектрисой 1-го и 3-го координатных углов, сама

биссектриса этой полуплоскости не принадлежит .

Упражнения

I.

Таблица (рис. 74) представляет собой граф ик дежурс тва

по комнате девушек, живущих в общежитии. Соответствие между

какими множествами устанавливае т эта таб лиц а? Что представляет

Рис. 74

113

собой к аж дая упорядоченна я пара, прин адл ежащая данному со

ответствию? Можно ли з адат ь другое соответствие м ежду данными

множествами? Как это сделать?

2. Учащийся запл атил за книгу 70 к., за тет радь 3 к., за каран

да ш 5 к., за кисточку 6 к., за резинку 4 к. Соответствие

между какими дву мя м ножествами при этом установлено?

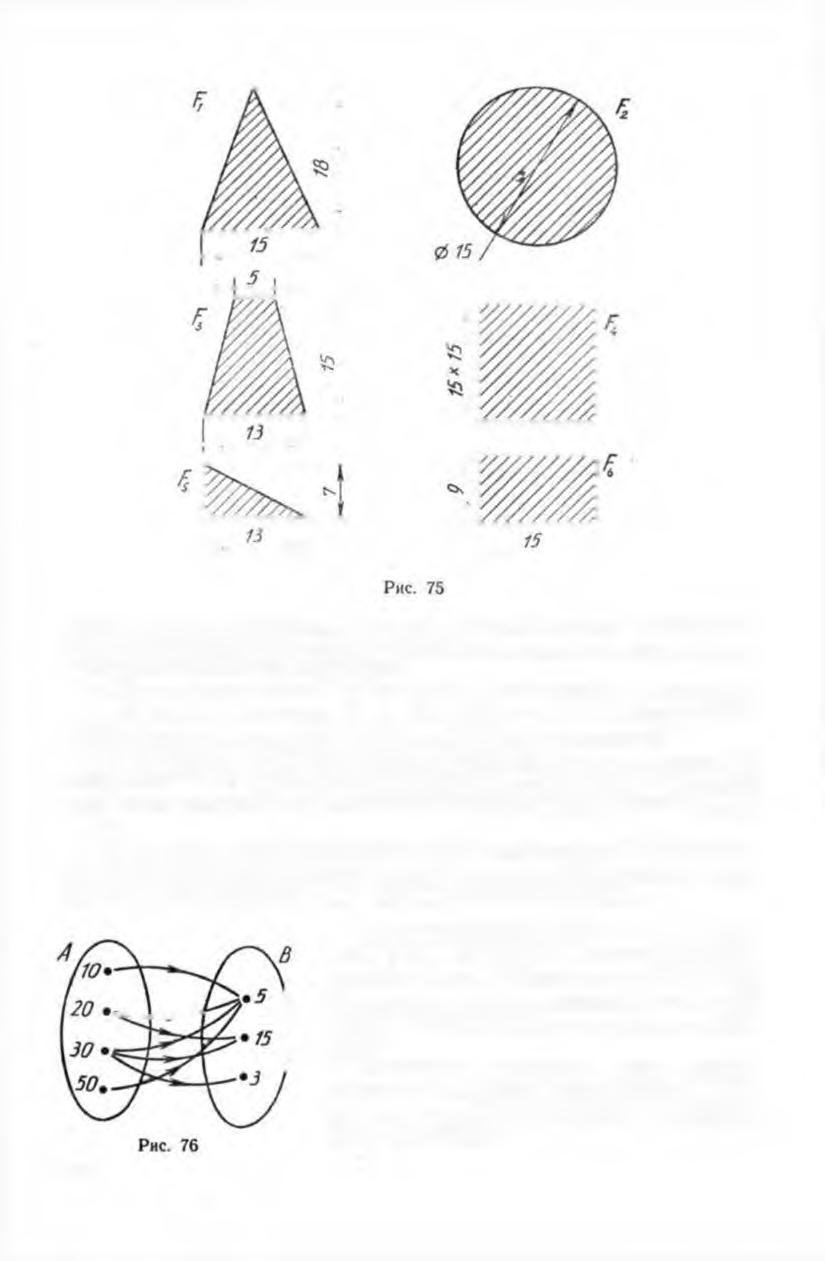
3. Вычислите площади фигур, изображенных на рисунке 75.

Соответствие между какими множествами установлено? Постройте

граф этого соответствия, обозначив каждую фигуру точкой Ft , Fi,

.... F6.

4. Н а рисунке 76 изобр аж ен граф соответствия Р. Запишите

все пары чисел, на ходящ ихся в этом отношении. Установите между

данными множествами А и В два других соотве тствия.

5. Д аны множества: М = {— 1, 1, — 2, 2,

— 3, 3, 0, — 4, 4) и N — множество нату

ральных чисел. Соответствие R между

элементами этих множ еств — «квадрат

числа т равен числу л», причем т ЈМ ,

nЈN.

Запиш ите множество пар, находя

щихся в заданном соответствии. Вер

но ли, что: 1) ( — 3,9 )ЈЯ ; 2) (0,0)6/? ;

3) ( - 4 , 16)6/??

114

6. Соответствие «меньше» зад ан о м ежду элементами множеств

Л = { 1, 2, 4, 6) и В = {5, 7}. Постройте граф ик этого соответствия.

Каким будет график соответствия «меньше на 1» между элементами

тех ж е множеств?

7. Элементы множеств Л"= {0, 1, 2, 3, 4, 5} и Y = Z находятс я

в соответствии «число х меньше числа у на 3», х ЈХ,

Какой из

нижеприведенных граф ик ов (рис. 77) явл яетс я графиком данного

соответствия?

8. На рисунке 78 приведен гр афик соот ветствия между м ножест

вами X и Y. Сколько пар чисел находится в заданном .соответ

ствии? Принад лежат ли множеству X числа 2; 0; 2,7; — 1,5, а мно

жеств у У числа 4; 0; — 1; 0,5? Находят ся ли в за дан ном соо твет

ствии пары чисел (0, 0), ( — 1, 4), ( —2, — 4)?

9. Графиком соответствия Р, зад анного между множествами

X и Y, является прямоугольник A BCD (рис. 79) . Назовите координа

ты трех точек, принад лежащих этому графику. Укажите характерис

тическое свойство чисел, принадлежащ их множествам Jf и К.

10. Д ан ы множества Х = [2, 5) и У= {3, 6}. Перечислите элементы

де картова произведения данных множеств и образуйте все подмно

жества полученного множества. Какое из подмножеств задае т

соответствие: 1) «больше»; 2) «меньше»; 3) «больше или равно»?

-1

Рнс. 78

4 X

/ 2 J $

Рис. 77

т т т г г

Рис. 79

II5

I I.

Приведите примеры за дан ий из начального курса м ате ма

тики, при выполнении которых рассматриваются соответствия

между:

1) множеством отрезков и множеством натуральных чисел;

2) множеством прямоугольников и множеством натуральны х чи

сел;

3) множеством уравнений и множеством натуральных чисел.