4. Требования к определ ению понятий
Ч тобы оц енить правильн ость явных опред елени й, над о зна ть
правил а определени я по нятий. Та к как преобла дающее б ол ьшин
ст во определений в школьном курсе мат ематики — это определе
ния через ро д и видовое отличие, то речь бу дет идти о правилах
этих опред елений.
Прежде всего определяемое и определяю щее понятия должны
быть соразмерны. Это зн ачит, что совокупности предмет ов, охва
тываемые ими, долж ны совпадать. Со разме рны, например, поня
тия «прям оугол ьник» и «четырехугольни к, в котором все углы
прямые». Если ж е об ъем определяющ его понятия включ ает в се бя
об ъем пон ятия опред еляемого , то говор ят об ошибке слишком
широкого определени я. Так, опред еление « П рямые а и b на зывают
ся пар аллельными, если они не имеют об щих точек или совп ада
ют» с лишком широк о, поскол ьку ему удо вл етво ряют и с крещива
ющиес я прямы е. Если же объем определяю щего по няти я у же
об ъема опр еде ляемого пон ятия, то имеет мес то ошибка слишко м
узкого оп ределения. Н а при мер , оп ределение « П ря мы е а и b
н азы ваются п а р а ллельн ыми , если они не им еют о бщих точек »
с лишком у зк о, по с кольку ему не у д о влетвор яют с овп адающие
прям ые.
Второе правило определ ения запрещает порочный круг: не льзя
о пр еделять понятие через с амо себя или о пред елять его чер ез
другое понятие, которое, в свою очер едь, о пред еляется через него.
Возьмем т акие пон ятия нач альной ма тематики, как «умно же ние»
и «произвед ение», и дадим им следующие опреде лени я:
Умножением чисел называется действие , при пом ощи которого
находят произвед ение этих чисел.
Произведением чисел называ ется рез уль тат их умножени я.
Видим, что ум но жение определяется чер ез пон ятие произ
ведения, а про изв еде ние — чере з понятие ум но жения. О пределе
ния образо вали, ка к говор ят в м ате мат ике , порочный круг. В pe
ll
Рис. 2
Рис. 3
зультате цепочка посл едова тельн ых опред елений, выс троенных
в р амках курс а, пр ерывает ся.
Порочным круг содержится и в тако м опре делении: «Решением
уравне ния на зы вается число, которое явл яе т ся его решением».
Здесь пон ятие «решение ур авнения» опред еляет ся, по сути дела,
че рез решение уравн ения.
Третьим ва жным требованием к логич ески правильному опре
дел ению поняти я явл яе тся сл едующее: в опре деле нии д ол жны
быть у казан ы все с во йства, по зволяю щ ие о д но значн о в ыделять
объек ты, п р ин а д л е ж а щ и е о бъему о пределяе мого пон ятия.
Ра ссмотр им, например, т ако е определ ение поня тия «см ежные
углы»: « См ежными называются углы, которые в сумм е составля
ют 180°». Нетрудно увид еть, что под данн ое опреде ление можно
подв ести не то лько углы, изо браженные на рисунке 2 и действи
тельно явл яю щиеся смеж ными, но и углы, изо бра жен ные на ри
с унке 3. П очему так произо шло? Дело в том, что в приведенном
опред елени и с межны х угло в у казано лишь о дно их свой ство, а
им енно свойство с оставлять в сумме 180°, но его нед оста точно
д ля вы деления смежных углов из всех других.
Еще одно требование к правильному определ ению понятия —
отсутствие в нем избыточности. Это о зна чает, что в опред елении
не д о лжно быть указано лишних свой ств, выт екающ их из д р у
гих свойс тв, т акже вкл юче нных в опр еделени е понятия .
Ра ссмотрим определени е: « Прямо уголь ником на зы вается че
тырехугольник, у которого пр отивоположны е стороны равны и все
углы пря мые ». Мож но пок азат ь, что включенное в оп ределение
свойст во «иметь пр отивополо жные равн ые ст ороны» вы тека ет из
сво йс тва «и меть пр ямые углы». Сле доват ельно, данно е о пр еделе
ние прямоу гольника избыточное и правильнее о пр еделять пр ям о
угольни к таким о бра зом: «Пр ямо угольником называется четырех
угол ьник, у которого все углы прям ые» .
Следу ет с казать, что в любом определ ении по нятия ест ь эл е
мент пр оизв ол а, что проя вл яется, во-п ервых, в выборе терм ина
(прямоугольн ик, в котором все сто роны равны, мог бы называться
и по-др угому), а во-вторых, в выборе свой ств, включаемых в оп
ределение . И принципе пон ятие квадрата можно опре делить так:
«Квадратом называет ся ромб, у кот орого все углы прямые» — или
так: « Квадратом на зы вается па раллелограмм , у которо го все
12
с
тороны рав ны, а углы прямые». Раз
личные опр едел ения одного
и того ж е понятия во змо жны потому, что из большого числа
свойств, в ход ящ их в с о д е ржани е этого пон ятия, в о пределение
вклю чаю т с я тольк о некото рые.
Если од ному и т ому же понят ию даются, например, два р а з
ных определени я, то они дол жны быть р авно сил ьными. Это о зна
чает, что из свойств, включенных в одно о пред еление, д олжны
вы текать с во йства, поло женные в основу д ругого определ ения,
и наоборот.
Чем же р уково дст ву ют ся, когда из возможных определений
не кото рого пон ятия вы бираю т одно? И сходят из того, ка кое опре
дел ение пр още, ес тес твеннее или це лес ообразнее д ля дальн ейшего
построения теории.
Если ж е ка кие -либо свойства о казы ваю тся включе нными в
определение, то другие свойс тва тех же о бъекто в могут быть л оги
чески выведены из тех, что вош ли в определение. Э то важ ное по
лож ение исп ользуют при решении за д ач на р аспо зна вание. Если
о бъект А прина длежит объему о пр еделяем ого понятия , то он
о б лад ает всеми с войс твами, которые у каза ны в о пред елении
понятия. Сп раведливо и обратное утвержд ение, т. е. если известно,
что объект А о бладает всеми свойствами, кото рые у каза ны в
определении по нятия, называемого некоторым термин ом, то и
объек т А мо жно н азвать этим термином.
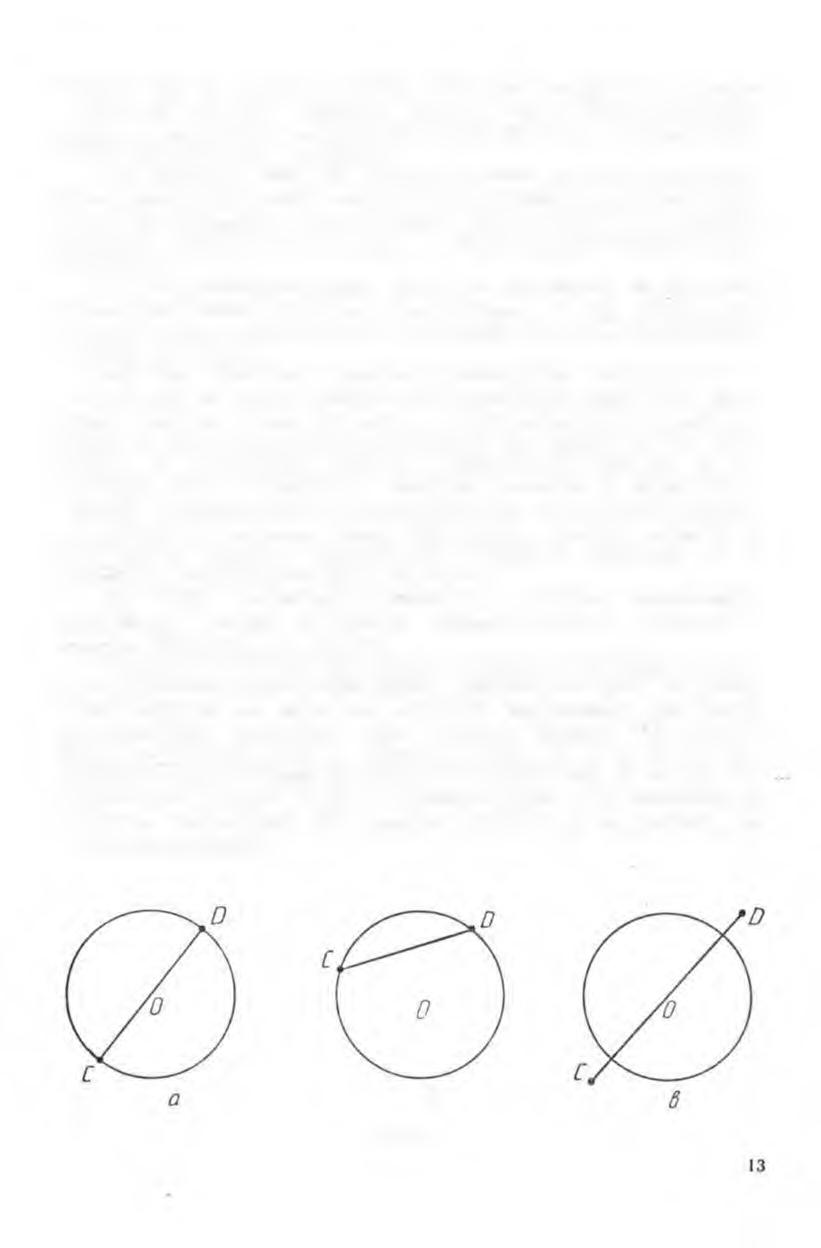
П р и м е р . И спол ь зу я о пре деление д иаметра окр ужности,
уста нови м, в каком из случаев, пред ста вл енных на рисунке 4,
отре зок CD являет ся диамет ром.
Опред елим диамет р окружности сле дующим о бра зо м: д иамет
ром окр ужност и называется хорда, про ходящая через ее центр .
Чтобы отре зок CD ока за л ся диаметром окр ужност и, достаточн о
одновр еменн ое вып олнени е двух усло вий: о трезок CD дол жен
быть хордой окр ужност и и проходить ч ерез ее центр. Этим д вум
условиям удовл етво ряет отрезок CD в слу чае «а». В случ ае «б»
отрезок CD — хорда, но он не проходи т через центр окружности;
в сл учае «в» о трезок CD проходит через центр окру жно сти, но
не являе тся хордой.
6
Рнс. 4
Ещ
е одним требо ва нием к логич ески
пр авильно му определе
нию понятия является следующее: необ ходимо, чтобы опр еделяе
мый о бъект с ущест вовал . Расс мотр им , например, тако е опред еле
ние: «Тупоуг ольным треугольником на зы вается треугольн ик, у
которого все углы тупые». Нет рудно у бедиться в том, что т реуго ль
ник, у которого все углы тупые, не су ществуе т. Следовате льн о,
данно му о пре деле нию реал ьно ничего не соот ве тствуе т, и поэтому
оно не мож ет счи таться логич ески прави льны м.
З а метим, что в м ате мат ике для отве та на вопрос, существуе т
ли объект, удо вл етво ряющий данном у определ ению, как пр ави
ло, доказываю т с пециальную теоре му, по дтвержд ающую во змож
ность с ущ ествова ния объекта, о кото ром го воритс я в опред елении.
В геометрии с ущ ествование о бъекта, удовлетворяющ его опред е
лению, иногда о бос но вывают построив его.
Упражнен ия
1. Сформулируйте о пр еде лени е пр ямо уголь ного треу гольника
и выявите его стр уктуру.
2. Уч ащийся оп реде лил пря мой угол ка к угол, стороны кото
рого вза им но пе рпе нд ику ляр ны, а взаи мно пер пе нд ику ляр ные
пр ям ые ка к прямые, о бра зу ющ ие при пересечении прямы е углы.
Каку ю о шиб ку допустил уч ащ ийс я?
Каким о бразом могут быть ознаком лены у чащиеся начальных
клас сов с понятием прямого угла?
3. У чащ ийс я по анал огии с опред елением остроугольного
тр еуго льника с форм улиро вал тако е опред еление о строугол ьного
чет ыр ехуго льни ка: « Остр оугольны м четыре хугольником н азы
ва ется выпуклый четырехугольник, все углы которо го острые».
Можно ли счит ать это опре делен ие пр авил ьным?
4. Один уч ащийся опре делил понятие прямоу гольника так :
«Пр ям оугол ьником на зы вается четырех угол ьник, у кот орого все
углы прямы е и сторон ы попарно ра вны».
Второй учащийся с каза л: « Прямоу гольником называе тся четы
рех уго льник, у которого все углы прямые».
И на конец , третий дал тако е опред еление: « Прямо уголь ни ком
на зы ва ется четырехугольник , у которого про тивополож ные с то ро
ны равн ы».
Какой из уч ащ ихся д а л пра виль ное опред елени е понятия пря
моуголь ника?
М ожно ли о преде лит ь это понятие ещ е каким-либо о бра зом?
5. В ка ких из привед енных ниже опред елени й мат ематичес ких
пон ятий имеются ошибки? И справьте их, если это во змо жно.
1)
Биссект рис ой тре уго льника на зы вается прям а я, д е лящая
угол т реу гольника пополам . 2) Диаметром круга на зыва ется
х орда , пр оходящая ч ерез центр круга . 3) Касательной к о к руж
ности на зыва ется пр ямая, ко тор ая касается о кружност и. 4) Р ом
бом называется пара л лелограмм, д ве смежные стороны которого
и
f2
Phc. 5
равны. 5) Сло жением называется действие , при котором числа
ск лад ываются, б) Ра внос торо нни м треугольником на зы вается
треугол ьник, у кот орого р авны все его стороны и все его углы.
7) П араллелограммом на зы вается много угольник, у которого
против оположные ст ороны поп арно па рал лельны.
6. П роанализи руйт е логи ческую структуру определе ния п ря
м оугольни ка (через четырехугольник) и уст ановите , ка кие из ф и
гур (рис. 5) явл яю тся прямоугольниками.
7. Д а йт е определени е биссектрисы углы и установ ите , на
ка ко м из рисунков луч 13D явл яе тся бис сектрисой у гл а (рис. 6 ).
8. Сф орму лируйте определени е понятия « квадрат» , у казав в
каче стве родово го поня тия «прямоугольник». П оль зуяс ь д анны м
оп ределением, укаж ите условия, при которых: 1) ф игу ра будет
явл яться ква дратом; 2) ф игу ра не буде т яв лять с я к вадратом .
9. Достаточно ли ниж еприв еде нное усл овие д ля того, чтобы
ч етырех угольни к был прямоугольником: I) он имеет две пары
па рал лельны х сторон; 2) три его угла яв ляются прямыми;
3) его диагона ли кон груэнтн ы; 4) д ве его сто роны па рал лельны?
10. Приведит е пример ы за дач на расп ознавание фигур и д р у
гих объекто в из учебников математики д ля началь ных кл асс ов.