§ 6. Отн ош ен ия и соотве тствия

36. Понятие отношения

В математик е изучают не только сам^объек ты (числа, фигуры,

величины), но и связи, отношения между ними. Так, усвоение

понятия натурального числа — одного из ведущих понятий началь

ной математики и математики вообще — происходит благо даря

изучению различных взаим освязей между числами. Например,

выяс няется, что:

число 5 больше числа 2;

число 10 больше числа 8 на 2;

число 7 следует з а числом 6, т. е. числа связаны различными

отношениями: «больше», «больше на», «следует за» и др.

В геометрии изучают паралле льность и перпендикулярность

прямых, равенство и подобие фигур, т. е. различные отношения

м ежду геометрическими объектами.

С равнивая множества, мы говорим, например, что они пере

секаются, или равны, или одно включено в другое, т. е. уст анавли

ваем отношения между множествами.

В математике чаще всего рассм атриваю т отношения между

двумя объектами. Их называют бинарными. В нашем курсе мы будем

изучать только такие отношения, поэтому в дальнейшем слово

«бинарные» будем опускать.

Пере д нами стоит задач а: имея представления о конкретных

отношениях между числами, геометрическими фи гурами, множества

ми и другими объектами, установить, что общего у этих отношений,

каким образом можно к ласси фицирова ть такое огромное число

самых разнооб разных отношений. Знание этого материала нужно

учителю начальных классо в для того, чтобы, изучая конкретные

отношения в на чальной школе, понимать их общность, взаим освяз и,

роль в усвоении тех или иных понятий.

Выясним сначала, что общего у различных известных нам

отношений.

Рассмотрим множество чисел ^ = { 3 , 4, 5, 6, 8}. М еж ду числам и

этого м ожества существует отношение «больше»: 4 > 3 . 5 > 3 , 6 > 3 ,

8 > 3 , 5 > 4 , 6 > 4 , 8 > 4 , 6 > 5 , 8 > 5 , 8 > 6 .

Можно рассмотреть дл я данных чисел и отношение «больше

на 1»: «4 больше 3 на 1», «5 больше 4 на 1», «6 больше 5 на 1».

Числа данного множества связаны такж е отношением «меньше

в 2 раза»: «3 меньше 6 в 2 раза» , «4 меньше 8 в 2 раза».

М ож но указать и другие отношения между числами 3, 4, 5, б

и 8, мы ограничимся тре мя, названными выше.

Об рати м внимание на следующее: рас см атри вая то или иное

отношение, мы кажд ый ра з оперировали упорядоченными па рами,

образованн ыми из чисел данного множества. Д л я отношения «боль

ше» это было множество {(4, 3), (5, 3), (6, 3), (8, 3), (5, 4), (6, 4),

(8, 4), (6, 5), (8, 5), (8, б)), дл я отношения «больше на 1» — ((4, 3),

98

(5, 4), (6, 5)} а дл я отношения «меньше в 2 раза» — множество,

со держ аще е две пары: {(3, 6), (4, 8)}. Таким образом, можно сказат ь,

что каждое из рассматриваемых отношений определяется м ножест

вом пар чисел, обра зованных из элементов множества Х = {3,

Известно, что упорядоченные пары — это элементы декарто ва

произведения множеств или его подмножеств. Нетрудно видеть,

что те множества пар, которые определяют отношения «больше»,

«больше на 1» и «меньше в 2 раза», явл яются подмножествами

декар това произведения Х Х Х = {(3, 3), (3, 4), (3, 5), (3, 6}, (3, 8),

(6, 4). (6, 5), (6, 6), (6, 8), (8, 3), (8, 4), (8, 5), (8, 6), (8. 8)).

Итак, к аж дое из рассматриваем ых отношений определяется

множеством пар, которое, в свою очередь явл яет ся подмножеством

дек артова произведения X X X.

Вместо того чтобы говорить, что отношение определяется мно

жеством пар, в математи ке само это множество пар называют

отношением между элементами множеств а X.

О п р е д е л е н и е . Отношением межд у элементами множества X

или отношением на множестве X называется всякое подмножество

декартова произведения X X X .

Отношения обозначаю т прописными буквами латинского а л фа

вита: Р, Q, R, S и др. Следовательно, если R — отношение между

элементами множества X, то R a X X X .

Отношения на конечном множестве X можно представлять н а

глядно, при помощи особых чертежей, состоящих из точек, соединен

ных стрелками. Такие чертежи на зывают графами1.

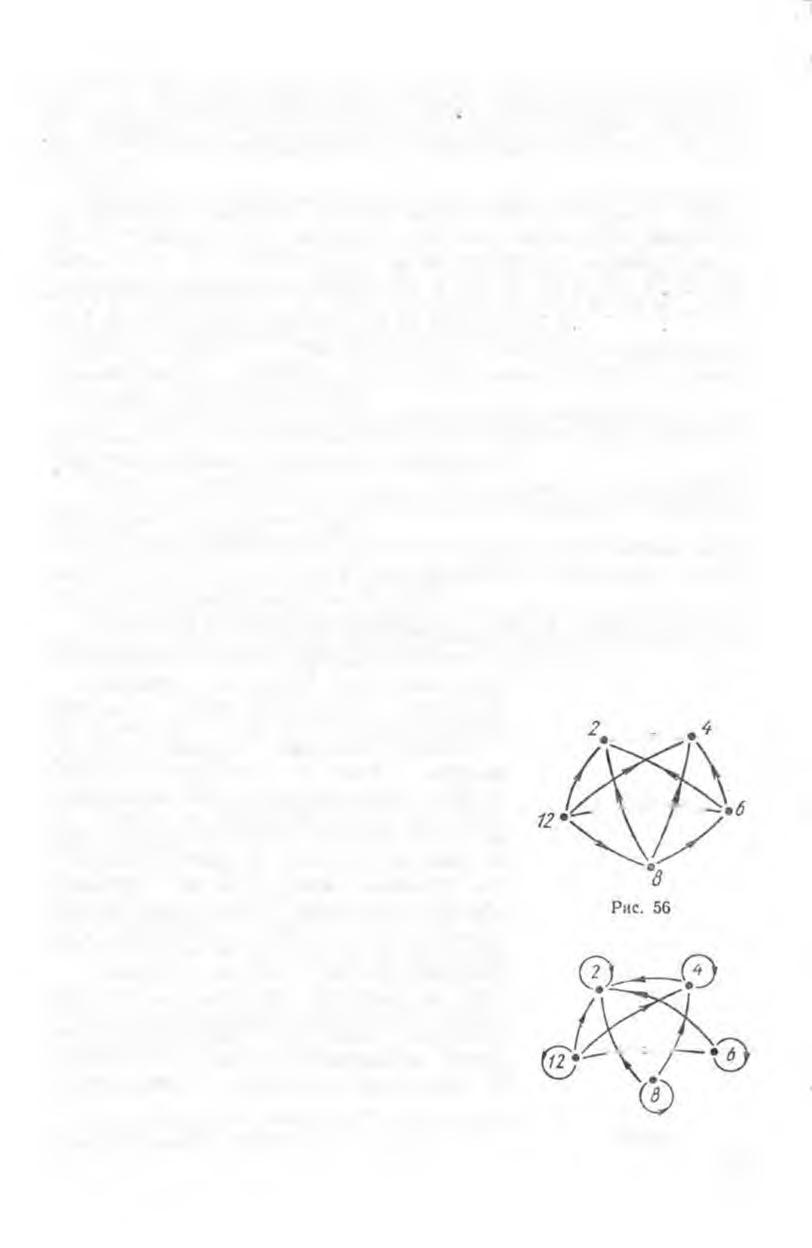
Построим, например, гр аф отношения

«больше» м ежду элементами множества

Х = (2, 4, 6, 8, 12). Д л я этого элементы

данног о м ножества изобразим точками и

соединим стрелками те точки, которые

изо бра жают числа, нахо дящиеся в отноше

нии «больше». Поскольку 4 > 2 , то прово

дим стрелку от 4 к 2; так как 6 > 4 , то

проводим стрелку от 6 к 4 и т. д., пока не

переберем все пары чисел, связан ных з а

данным отношением. В результате получаем

граф отношения «больше» для элемен

тов множества Х = [2, 4, 6, 8, 12} (рис. 56).

Рассмотрим теперь на том ж е множестве

X отношение «кратно» и построим его граф.

Аналогично предыдущему случаю изобразим

элементы множе ства X точками и соединим

стрелками те, которые изо бражают числа,

находящиеся в отношении «кратно»: 12

1 Слово «граф», так ж е как и слово «график», проис

ходит от греческого слова «графо» — пишу.

4*

Рис. 57

99

кратно 2, 12 кратно 4 и т. д. Так как любое число из множества X

кратно самому себе, то граф даного отношения будет иметь стрелки,

начало и конец которых совпадут (рис. 57). Такие стрелки на графе

называют петлями.

Упражнения

1. Приведите примеры отношений, существующих между:

1)

натуральными числами; 2) прямыми на плоскости; 3) тре

угольниками; 4) множествами.

2. Из элементов м ножества Х = {0, 3, 6, 9, 12, 15, 18) образуйте

всевозможные пары чисел так, чтобы компоненты пары (х, у) были

связ аны отношением:

1)

«х больше у в 3 раза» ; 2) «х больше у на 3». Постройте графы

данных отношений.

3. Какое из следующих множеств явл яется отношением между

элементами мн ожества Л = { 0, 3, 6, 9, 12):

1) Р — {(6, 3), (9, 3), (12, 3), (12, 6), (3. 3), (6, 6), (9, 9), (12, 12)};

2) Т = ((3, 3), (3. 6), (3, 9), (3, 12), (6, 6), (9, 9), (12, 12));

3) М = ((3, 6), (6, 12), (9, 18))?

4. Установите, какой из гр афов, приведенных на рисунке 58,

является графом отношения « х — делитель числа у», за данног о

на множестве В = (5, 10, 20, 30, 40).

5. На мн ожестве ^ = {0, 2, 4, 6, 8) заданы отношения Р, Q, S.

Постройте их графы, если:

Р — отношение «меньше»;

Q — отношение «меньше в 2 раза »;

S — отношение «меньше на 2».

6. Множество М членов семьи Волковых состоит из отца

Михайла Петровича, матери Веры Ивановны и детей: Толи, Кати,

Пети и Оли. М ежду членами семьи существуют различные отноше

ния родства. Постройте графы отношений: 1) «быть дочерью»;

2) «быть братом»; 3) «быть матерью».

Рис. 58

100

7.

На рисунке 59 дан граф отно

шений «быть братом» на множестве

детей, живущих в одном доме (де

ти обозначены точками А, Б, В, Г,

Д , Е, Ж , 3) . Кто из них яв ля

ется девочкой, а кто мальчиком? О

ком из ребят по этому графу нельзя

ничего сказат ь?