27. Пересечен ие множеств

Из элементов двух и более множеств можно образовать новые

множества. Считают, что эти новые множества явл яю тся результа

том операций над множествами, которые, в свою очередь, следует

рассматривать как обобщение операций, выполняемых над раз

личными совокупностями. В частности, таких, как нахождение об

щих элементов двух и более множеств, объединение двух и более

совокупностей в одну, удаление из совокупности ее части в другие.

Пусть даны два множества: А = {2, 4, 6, 8} и В = {5, б, 7, 8, 9).

Образуем множество С, в которое включим общие элементы мно

жеств А и В: С = |6, 8). Так, полученное множество С называют

пересечением множеств А и В.

О п р е д е л е н и е . Пересечением множеств А и В называется

множество, содержащее только такие элементы, которые принад

леж ат множеству А и множеству В.

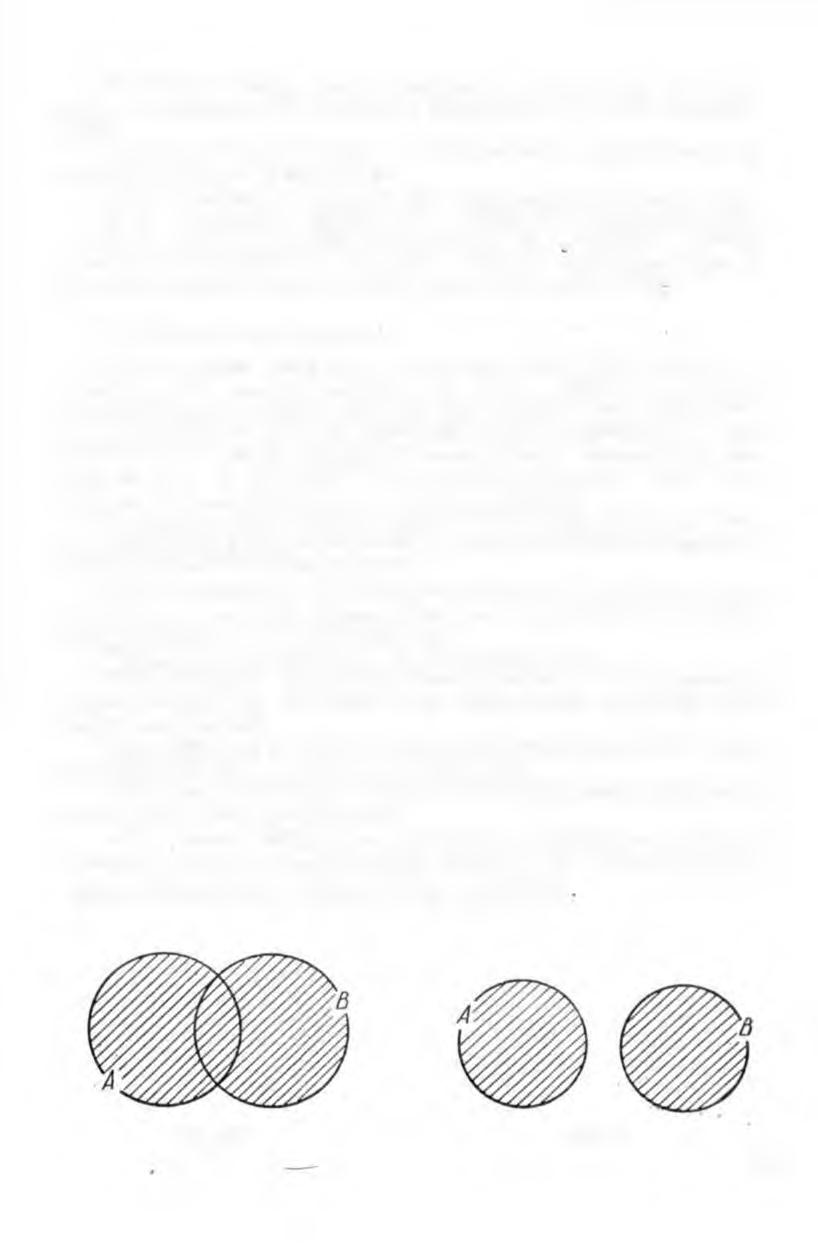
Пересечение множеств А и В обозначаю т Л("|В. Если изобра

зи ть множества Л и В при помощи кругов Эйлер а, то пересе

чение данных множеств изобразится заштрихованной областью

(рис. 28). В том случае, когда множества Л и В не имеют

общих элементов, говорят, что их пересечение пусто и пишут:

/ 1 П В = 0 .

Операция, прн помощи которой находят пересечение множеств,

называется та кже пересечением.

Как находят пересечение множеств в конкретных случа ях?

Прежде чем р ассматривать примеры, заметим, что согласно опре

делению пересечения х Ј Л Г | В о х ЈА и хЈ В

Если элементы множеств Л и В перечислены, то, чтобы найти

Л ПВ, достаточно перечислить элементы, которые принадлежат Л и

В, т. е. их общие элементы.

А как быть, если множества заданы при помощи характери

стических свойств их элементов?

Из определения следует, что характеристическое свойство множе

ства А (~|В составляется из характеристических свойств пересекаемых

множеств с помощью союза «и».

Найдем, например, пересечение множества А — четных натураль

ных чисел и множества В — двузначных натуральных чисел. Х арак

теристическое свойство элементов мно

жества А — «быть четным нату раль

ным числом*, характеристическое свой

ство элементов множества В —

«быть двузначным натуральным чис

лом». Тогда, согласно определению,

элементы пересечения данных мно

жеств должны обладать свойством

«бы ть четным и двузначным натураль

ным числом». Таким образом, множест-

71

Рис. 29

В, будут элементы

лпв =в.

Упражнения

во Л|"|В состоит из четных двузначных чи

сел (союз «и» в данном случае можно опус

ти ть ). Полученное множество не пусто.

Например, 24ЈЛ ПВ , поскольку число 24

четное и двузначное»

Выясним теперь, что представляет собой

пересечение множества А — четных нату

ральных чисел и множества В — натураль

ных чисел, кратных 4. Данные множества А

и В бесконечные, и множество В — подмно

жество множества А. Поэто му элементами,

принадлежащими множеству А и множеству

множества В (рис. 29). Следовательно,

1. Сформулируйте условия, при которых истинны следующие

вы сказывания: 1) 5 ( M f|B; 2) 7Ј А (]В.

2. Известно, что хЈА. Следует ли отсюда, что л :ЈЛ ПВ?

3. Известно, что х Ј А (]В. Следует ли отсюда, что х ЈЛ ?

4 . А — множество точек окружности, В — множество точек пря

мой /. Из скольких элементов может состоять пересечение данных

множеств? Может ли оно быть пустым? Изобразите возможные слу

чаи на чертеже.

5. Запишите множество S чисел, являю щихся однозначными и

четными. Пересечением каких множеств оно является?

6. Изобразите при помощи кругов Эйлера пересечение мно

жеств А и В, если: 1) Л с г В ; 2) Вс= Л ; 3) А ( ] В — 0-

7. Найдите пересечение множеств Л и В, если:

1) Л ={а, Ь, с, d, е. Я;

2) Л ={26. 39, 5, 58, 17, 81|;

3) Л ={26, 39. 5, 58, 17, 81);

B = {f>, е, f, к, /];

В = {17, 26, 58);

В = {2, 6, 3. 9. 1, 7).

8. Из каких элементов состоит пересечение множества букв

в слове «математика» и множества букв в слове «геометрия»?

9 . М — множество однозначных натуральных чисел, Р — мно

жество нечетных натуральных чисел. Какие числа войдут в пе

ресечение данных множеств М и Р ? Содержатся ли в нем числа

1,5 и 17? Ответ запишите, используя символы Ј и

10. Найдите пересечение множеств решений неравенств, в ко

торых переменная — действительное число: 1) х > — 2 и х > 0;

2) х > — 3,7 и х < 4 ; 3) х~^Ъ и х < — 7,5; 4) — 2 < * < 4 и х ^ — 1;

5) — 7 < х < 5 и — 6 < * < 2 .

11. Начертите два треугольника так, чтобы их пересечением:

1) был треугольник; 2) был отрезок; 3) была точка; 4) был

многоугольник.

12. Как ая фигура может получиться в пересечении треуголь

ника и четырехугольника? Рассмотрите несколько случаев.

72

13. Сколько точек может ока заться в пересечении: 1) пря

мой и окружности; 2) отрезка и окр ужности; 3) двух окружно

стей?

14. Начертите две фигуры, принадлежащие пересечению мно

жеств С и А, при условии, что:

1) С — множество квадратов, D — множество прямоугольников;

2) С — множество ромбов, D — множество прямоугольников.

15. А — множество решений уравнения 3 *- } - * /= 15, В — множе

ство решений уравнения 2 * - f y = l l. Найдите множество точек С

решений системы этих уравнений. Верно ли, что С = Л["|Д?