2.3 Оцінювання невідомих параметрів у багатофакторній регресії

Запишемо вибіркову регресійну багатофакторну модель

y_i=b₀+b₁x_1i+...+b_px_pi+e_i, (4.42)

у матричному вигляді

y=Xb+e (4.43)

де b – вектор-стовпець параметрів, оцінених за МНК; е - вектор-стовпець помилок розміру.

Вектор невідомих параметрів ми знаходимо за МНК, мінімізуючи суму квадратів залишків

e’e=(y-Xb)’(y-Xb)= y’y-2b’X’y+b’X’Xb (4.44)

де вектор помилок виражено з (4.43) і враховано, що (Xb)’=X’b’; b’X’y=y’Xb

Прирівнявши нулю часткові похідні, ми отримаємо нормальну систему (р+1) рівнянь з (р+1) невідомими

(4.46)

Розпишемо (4.46) у матричному вигляді

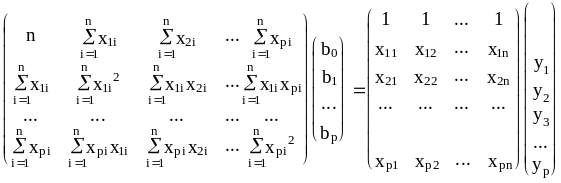(4.47)

або скорочено

X’Xb=X’y. (4.48)

Якщо зворотна матриця (Х’Х)^-1 до (Х’Х) існує, то помноживши обидві частини (4.48) на цю матрицю, отримаємо

(Х’Х)^-1(Х’Х)= (Х’Х) ^-1Х’у (4.49)

де (Х’Х)^-1(Х’Х)=І –одинична матриця розміру (р+1)(р+1), щ о дає

bІ= (Х’Х) ^-1Х’у; b=(Х’Х) ^-1Х’у (4.50)

Рівняння (4.50) є фундаментальним результатом для визначення невідомих параметрів у матричному вигляді. Вектор невідомих парамертів може бути отриманий з (4.50) або (4.44) шляхом диференціювання за кожним параметром (b₀, ..., b_p) та прирівнювання часткових похідних до нуля.

2.4 Дисперсійно-коваріаційна матриця параметрів регресії

За означенням дисперсійно-коваріаційна матриця для b є

var-cov(b)=E{[b-E(b)][b-E(b)]’

що можна записати

var-cov(b)= (4.51)

Можна показати (доведення не наводимо), що

var-cov(b)=²(X’X)^-1 (4.52)

де ² – дисперсія випадкової величини.

Можна показати, що оцінена дисперсія у випадку багатофакторної регресії дорівнює

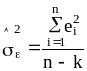(4.53)

або у матричному вигляді

,

де n-k – ступені вільності для SSE.

Обчислимо е’е. У випадку простої регресії, тобто однієї незалежної змінної

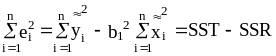(4.54)

Для двох незалежних змінних вираз (4.54) приймає вигляд

(4.55)

Узагальнюючи (4.54) та (4.55) на випадок р незалежних змінних, можна записати

(4.56)

де y^_i=y_i-y; x^_ij=x_ij-x_j

У матричному вигляді та можна записати

(4.57)

(4.58)

де ny²– відоме під назвою “корекція на середні значення”.

З (4.57) та (4.58) отримаємо

e’e=y’y-b’X’y (4.59)

За встановленим значенням е’е легко обчислити оцінку дисперсії випадкової величини, а використовуючи (4.53), легко знайти оцінені значення дисперсійно-кореляційної матриці (4.51).

2.5 Перевірка гіпотез щодо параметрів багатофакторної регресії у матричному вигляді

Одним з важливих припущень у багатофакторному регресійному аналізі є припущення про нормальний закон розподілу випадкової величини з нульвим математичним сподіванням і постійною дисперсією ², яке у матричному вигляді записується

N(0, ²I),

де  та 0 є векторами-стовпчиками розмірності (nx1), а І – одиничною матрицею розмірності (n x n).

Можна показати, що у випадку багатофакторної регресії кожний параметр також відповідає нормальному розподілу

b N(, ² (X’X)^-1) (4.60)

з математичним сподіванням, яке дорівнює значенню параметра узагальненої регресії , та дисперсією, що дорівнює дисперсії випадкової величини ², помноженої на відповідний діагональний елемент зворотної матриці. Оскільки справжнє значення дисперсії випадкової величини невідоме, ми замінюємо його на оцінку дисперсії. Така заміна приводить до того, що кожен елемент вектора (4.60) відповідатиме вже t-розподілу Cт’юдента з (n-k) ступенями вільності, що дає нам змогу обчислити t–статистику для кожного параметра

t=(b_i-_i*)/^²_bi з df=n-k. (4.61)

де _i* гіпотетичне значення, яке має прийняти параметр _i; b_i - оцінка параметра _i, отримана МНК.

Оскільки в економетриці поширеною формою нуль-гіпотези є Н₀: *_і=0, то t–статистика приймає вигляд

t*=b_i/^²_bi.(4.63)

Якщо t* потрапляє у критичну зону, то нуль-гіпотеза відкидається, а якщо не потрапляє – то з ймовірністю (1-)100% оцінка є статистично незначимою.

У багатьох програмах поряд із значенням b_i видають значення оцінки стандартного відхидення та відношення між b_i і цією оцінкою, що відповідає (4.63).

Інтервали довіри для параметрів багатофакторної регресії після визначення за t-таблицею Ст’юдента критичного значення розраховуються за формулою

_i=b_it_/2^_bi