Поняття про ступені вільності

Повернемося до виразу (2.29) та (2.29 a). Кожна сума квадратів пов`язана з числом, яке називають “ступенем вільності”. Це число показує, скільки незалежних елементів інформації, що утворилися з елементів у₁, у₂, ... у_n , потрібно для розрахунку даної суми квадратів.

Устатистиці кількістю ступенів вільності певної величини часто називють різницю між кількістю різних дослідів і кількістю констант, встановлених в результаті цих дослідів, незалежно один від одного. Окреме застосування цього поняття відноситься до суми квадратів.

Для утворення SST потрібно (n-1) незалежних чисел, тому що з чисел {(y₁-y), (y₂-y), ... (y_n-y)} незалежні тільки (n-1) завдяки властивості

SSR отримують у розглянутому випадку регресії, використовуючи тільки єдину незалежну одиницю інформації, яка утворюється з у₁, у₂, ... у_n, а саме b₁. Для ілюстрації цього запишемо відхилення, що пояснює регресію, у вигляді

З (2.41) маємо

Отже можна утворити, використовуючи одну одиницю незалежної інформації – b₁. В разі багатофакторної регресії ситуація буде інша. Звідси SSR має один ступінь вільності. У даному випадку ступінь вільності збігається з кількістю незалежних змінних, що входять до регресійної моделі.

SSE базується на кількості ступенів вільності, яка дорівнює різниці між кількістю спостережень і кількістю параметрів, що оцінюються. У разі простої лінійної регресії оцінюються два параметри b₀ та b₁. Якщо було проведено n спостережень, то SSE має (n-2) ступенів вільності.

Ступені вільності прийнято позначати через DF, або Df, або df.

У разі простої лінійної регресії ступені вільності, як і суми квадратів, можна розкласти таким чином

n-1=1+(n-2) (2.45)

Простий anova-аналіз. Аніліз дисперсій.

Введемо поняття про середні квадрати.

Середнім квадратом називається сума квадратів, поділена на відповідний їй ступінь вільності.

Середнім квадратом помилок називається сума квадратів помилок, поділена на відповідний ступінь вільності, якмй позначається через MSE.

У разі простої лінійної регресії середній квадрат помилок має вигляд

MSE= (2.48)

Середній квадрат, що поясніє регресію, позначається через та відповідно дорівнює

MRS=

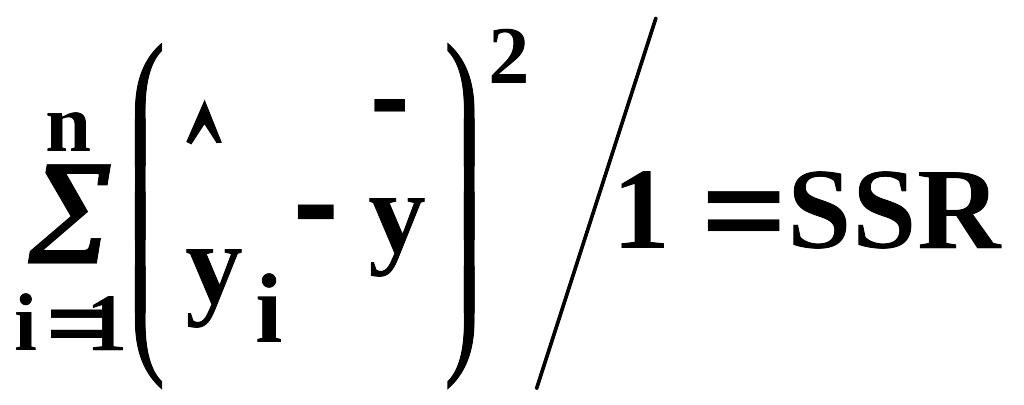
(2.47)

Для загальної суми квадратів середній квадрат не розраховується.

Базовою таблицею дисперсійного аналізу (ANOVA-таблицею) є таблиця, у яку зведені суми квадратів, пов`язані з певним джерелом варіації, ступенями вільності і середніми квадратами

Таблиця

ANOVA-таблиця

Джерело варіації	Кількість сту-пенів вільності	Сума квадратів	Середні квадрати
Зумовлено регре-сією (модель)	1	SSR=	MRS=
Непояснювальне за допомогою регре-сії (помилка)	n-2	SSE=	MSE=
Загальне	n-1

6. Перевірка адекватності моделі.

t- тест Ст`юдента

У загальному випадку довільну випадкову величину x_i, розподілену за нормальним законом розподілу з математичним сподіванням a та дисперсією можна звести до нормально розподіленої величини z_i з математичним сподіванням 0 і дисперсією 1 шляхом перетворення

z_i=(x_i-a)/_x (2.98)

Якщо у (2.98) замість невідомої дійсної дисперсії викоористаємо її оцінку, то при невеликій кількості даних (n<30) ми перейдемо до іншого t-перетворення і у загальному випадку матимемо

t_i=(x_i-a)/^_x (2.99)

де x_i- нормально розподілена величина з математичним сподіванням а і дисперсією _х² , t_i - випадкова величина, розподілена за t-законом розподілу Ст`юдента з n-1 ступенем вільності, де ступені вільності розраховуються за виразом оціненої дисперсії

Перетворення (2.99) для випадкової величини х, якщо мати на увазі, що вона розподіляється за нормальним законом розподілу з математичним сподіванням а і дисперсією _х²

(2.100)

де t- випадкова величина, яка розподілена за законом розподілу Ст`юдента з (n-1) ступенями вільності.

t- розподіл - це симетричний розподіл із середнім 0 і дисперсією (n-1)/(n-3), яка наближається до 1, коли n велике. Тобто в разі n t-розподіл наближається до нормального закону розподілу.

Для використання t-тесту Ст`юдента необхідно:

- обрати бажаний рівень значимості (від 1 до 10%);

- визначити кількість ступенів вільності;

- визначити критичне значення t за таблицями у залежності від рівня значимості та кількості ступенів вільності, яке поділяє усю множину на дві підмножини: множину, яку ми відкидаємо, і множину, яку ми приймаємо при заданому рівні значимості;

- розрахувати t-статистику t*;

-порівняти t* з t критичним.

Якщо t* потрапляє в критичну зону, можливі два випадки - нуль-гіпотеза правильна, але сталася малоймовірна подія, або нуль-гіпотеза неправильна. Ми вважатимемо найпростіше - нуль-гіпотеза неправильна, тобто відкидаємо її.

t-тест Ст`юдента для перевірки на значимість параметрів b₀ і b1,

визначених за методом найменших квадратів

Для перевірки на значимість параметрів b₀ і b1, визначених за методом найменших квадратів:

1. За формулами (2.81) та (2.86) обчислюємо оцінки дисперсій параметрів b₀ та b₁, використовуючи розраховану за формулою (2.93, а) оцінку дисперсії випадкової величини.

2. Будуємо t-статистику для кожного параметра за формулою

з (n-k) ступенями вільності (2.101)

де b_i- оцінка параметра , отримана за МНК; _i^*- гіпотетичне значення, якого має набути параметр _i (тобто нульова гіпотеза H₀: _i =_i^*); - оцінка дисперсії параметра b_i (з регресії); n - розмір вибірки (кількість спостережень); k - загальна кількість оцінених параметрів (k=2 у нашій моделі, бо ми використовуємо 2 ступені вільності, щоб оцінити 2 параметри b₀ і b₁).

У економетриці поширеною формою нуль-гіпотези є така

H₀: _i^* =0

проти альтернативної гіпотези

H₁: _i^* 0.

В такому разі t-статистика для параметрів має вигляд

t*=b_i/ (2.102)

Ця статистика є відношенням b₁ до оцінки свого стандартного відхилення, або, інакше кажучи, до свого середньоквадратичного відхилення.

3. Задаємо рівень значимості  і за таблицями знаходимо критичне значення t_кр для  100% та (n-k) ступенями вільності.

4. Якщо t* не потрапляє в критичну зону (-t_кр <t< +t_кр), то ми можемо стверджувати, що з ймовірністю (1-) оцінка параметра є статистично незначимою, тобто ми приймаємо нуль-гіпотезу. В іншому випадку нуль-гіпотеза відкидається і приймається гіпотеза Н₁, що в разі простої лінійної регресії також означає значимий вплив х на зміну у.

Т-тест може бути спрощений, бо значення t змінюються дуже повільно і приблизно дорівнюють 2, коли кількість ступенів вільності (n-k) більша, ніж 8. Тому, якщо (n-k)>8, ми відкидаємо нуль-гіпотезу при t*>2.

Для того, щоб оцінити зв`язок b₁ і b₀ з ₀ і ₁ потрібно аналогічно побудувати інтервали довіри. Спочатку розраховується -статистика за (2.101), а потім для заданого рівня значимості  за таблицями знаходимо t_/2 з (n-2) ступенями вільності. Тоді

_i=b_it_/2 з ймовірністю (1-).

Тест Фішера для перевірки нуль-гіпотези ₁=0

Тестування цієї гіпотези показує, чи дійсно незалежна змінна х впливає на у, тобто перевірка гіпотези ₁=0 відповідає перевірці адекватності моделі за F-критерієм Фішера.

(2.106)

Порядок тестування за критерієм Фішера аналогічний порядку тестування за критерієм Ст`юдента. Нульову гіпотезу відкидаємо з 100% ризиком помилитися, якщо розраховане за формулою (2.106) значення F>F_(1-)(1, n-2), яке визначається за таблицями відповідно до (1, n-2) ступенів вільності для простої лінійної регресії.

Якщо порівняти критерії Фішера та Ст`юдента, то

F-відношення= (t-відношення)² (2.112)

З математичної статистики відомо також, що

F-критичне значення= (t-критичне значення)² (2.113)

З (2.112) і (2.113) випливає, що ці два тести еквівалентні.

F-статистику можна записати ще іншим чином. Оскільки

SSR=R²SST; SSE=(1-R²)SST

то

F= (2.114)

7. Проведення досліджень та аналіз результатів

Прогнозування за моделями простої лінійної регресії

Якщо побудована нами модель адекватна, то ми можемо отримати два типи прогнозів:

1. Точковий прогноз для відповідного значення х_n+1 з побудованої вибіркової моделі

(2.115)

При цьому, виходячи з узагальненої моделі, дійсне значення у для прогнозного періоду дорівнюватиме

(2.116)

де _n+1- значення випадкової величини, не спостережуваної в n+1 періоді.

Отже, прогнозне значення є оцінкою дійсного значення змінної y_n+1 і за нашою вибірковою моделлю легко можна знаходити будь-яке прогнозне значення, яке буде точковим.

2. Інтервальний прогноз - інтервал, у який з певною ймовірністю потрапляє дійсне значення залежної змінної. Для інтервального прогнозу потрібно побудувати інтервали довіри для залежної змінної.

Помилка прогнозу обчислюється за виразом

e_n+1=y_n+1- _n+1=_n+1-(b₀-₀)-(b₁-₁)x_n+1 (2.117)

Математичне сподівання помилки прогнозу E(e_n+1)=0, бо за припущенням E(_n+1)=0, ₀ та ₁ є константами і E(b₀)=₀; E(b₁)=₁.

Піднесемо до квадрата обидві частини (2.117), встановимо математичне сподівання та визначимо значення дисперсії помилки

var(e_n+1)=E(e²_n+1)=var(_n+1)+var(b₀)+x²_n+1var(b₁)+2x_n+1cov(b₀,b₁) (2.118)

Враховуючи, що варіація помилки має бути мінімальною, знаходимо інтервал довіри у_n+1

(2.122)

Таким чином, (2.122) дає нам інтервал довіри для дійсного значення залежної змінної, але, враховуючи випадковий характер _n+1 , не має великого сенсу прогнозувати точне значення y_n+1. Тому на практиці частіше застосовується побудова інтервалів довіри для математичног о сподівання y_n+1, тобто

E(y_n+1)=₀+₁x_n+1 (2.123)

У такому разі, помилка прогнозу і дисперсія помилки відповідно дорівнюватимуть

e_n+1=E(y_n+1)- _n+1= -(b₀-₀)-(b₁-₁)x_n+1

var(e_n+1)= (2.124)

Інтервал довіри для E(y_n+1) при 100%-ному рівні значимості має вигляд

b₀+b₁x_n+1t_/2 (2.125)

Властивості МНК

Критерії для аналізу методів оцінювання в економетриці:

1. Відсутність відхилення, під яким розуміється різниця між очікуваним і дійсним значенням параметра E(b)-=0. Оцінювання без відхилення є важливою властивістю, але не за своїм змістом, а в комбінації з малою дисперсією.

2. Найменша дисперсія. Символічно b є найкращою, якщо var(b)<var(b*), де b* є іншою, не обов`язково без відхилення оцінкою .

3. Ефективність. Оцінка є ефективною, якщо вона має властивості 1 і 2, тобто є найкращою серед оцінок без відхилень.

4. Найкраща лінійна оцінка без відхилення (BLUE -best linear unbiased estimator). Оцінка є BLUE, коли вона без відхилень має найменшу дисперсію та є лінійною функцією від спостережуваних значень.

5. Найменша середня квадратична помилка MSE. MSE-критерій є комбінацією властивостей оцінок без відхилень та мінімальною дисперсією. Оцінка є мінімальною MSE-оцінкою, якщо вона має найменше значення MSE=E(b-)² . Можна довести, що дорівнює MSE дисперсії оцінки плюс квадрат відхилення.

6. Достатність. Оцінка є достатньою, якщо вона використовує всю вибіркову інформацію. Достатність сама по собі не є важливою ознакою, але вона є необхідною умовою ефективної оцінки.

Якщо виконуються основні припущення щодо випадкової величини , то оцінки, розраховані за МНК є лінійними, без відхилень, мають найменшу дисперсію з усіх можливих методів оцінювання. Тобто, метод МНК є найкращим для оцінювання невідомих параметрів простої лінійної регресії.

БАГАТОФАКТОРНА РЕГРЕСІЯ