Графік і таблиця нормального закону розподілу

Функція щільності нормального закону розподілу симетрична відносно осі z = 0, тому вся площина під кривою зліва від нуля також дорівнює 0,5. Це дозволяє шляхом досить легких перетворень отримувати ймовірності, які не передбачені в наведеній вище таблиці.

Наприклад, P(z 1.84) = 0.5+ P( 0 z 1.84) = 0.5 +0.4671 = 0.9671.

ДОДАТОК 2

Графік і таблиця f-розподілу Фішера

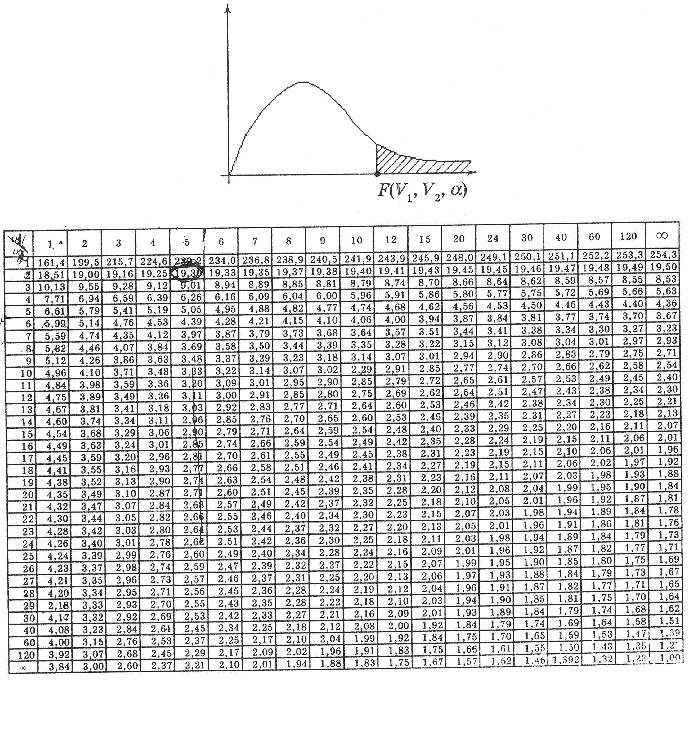
ДОДАТОК 3

Графік і таблиця t-розподілу Ст’юдента

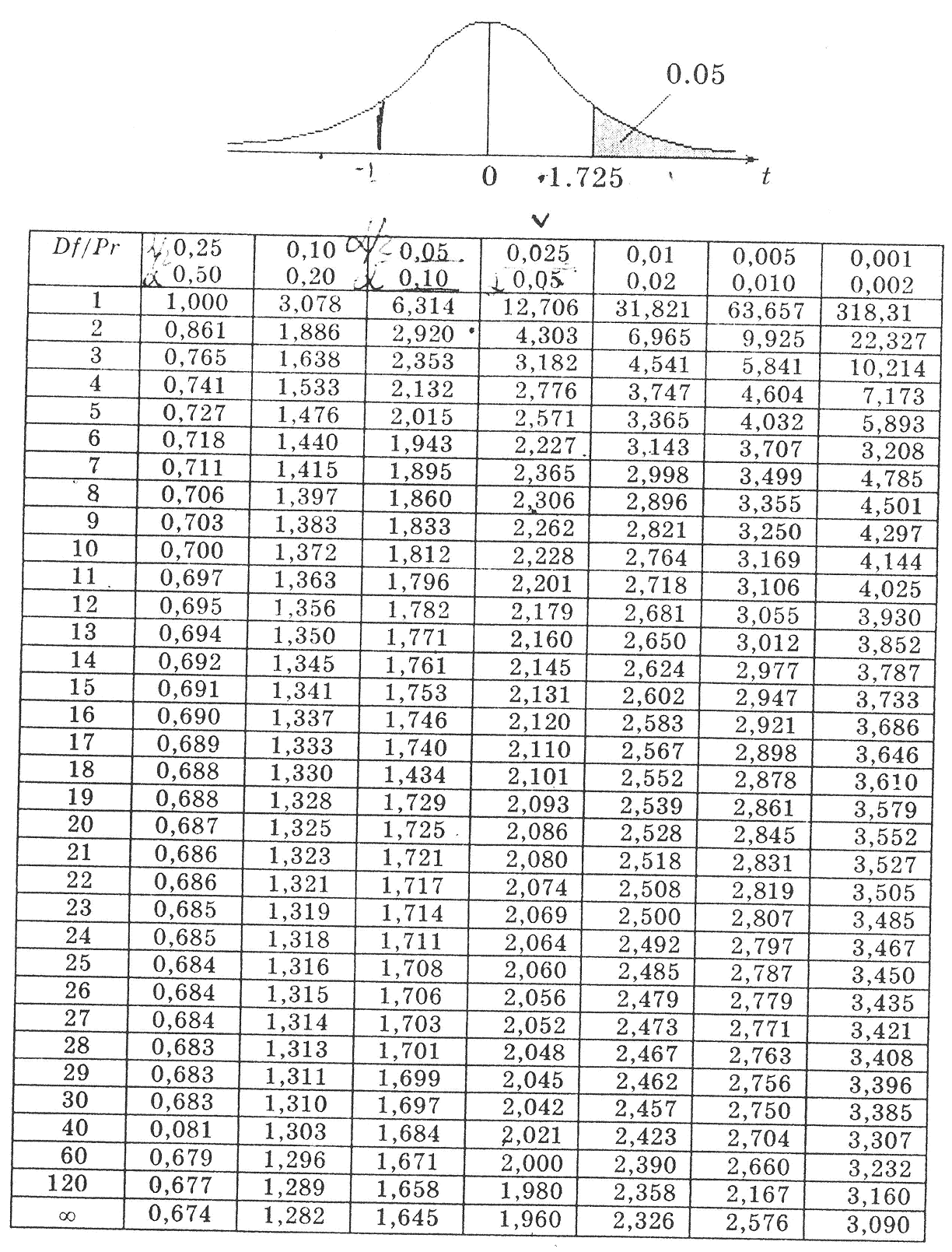
Приклад. Для df = 20

Pr (t > 2,089) = 0,025;

Pr (t >1,725) = 0,05;

Pr (| t | > 1,725) = 0,10.

ДОДАТОК 4

DW-статистика Дарбіна – Уотсона.

Критичні точки та при рівні значимості d = 0.05

ДОДАТОК 5

DW-статистика Дарбіна – Уотсона.

Критичні точки та при рівні значимості d = 0.01

5.3. Автокореляція

5.3.1. Природа автокореляції. Основні поняття та означення

Одним із припущень класичного регресійного аналізу є припущення про незалежність випадкових величин. Якщо це припущення порушується, то мимаємо справу з автокореляцією. Звичайно, важливо зрозуміти, що викликає автокореляцію, які її практичні та теоретичні наслідки, чи змінюються методи знаходження невідомих параметрів моделі в умовахавтокореляції і, нарешті, чи є ефективні методи її тестування.

Спробуємо послідовно відповісти на всі ці запитання. Як уже зазначалося вище, в регресійній моделі автокореляція наявна у разі, коли випадкові величини залежні між собою, тобто: Е( ) 0 ,і j.

Потрібно розрізняти поняття автокореляції і серійної кореляції. Автокореляцією називається залежність між значеннями однієї вибірки з запізненням в один лаг. Наприклад, якщо між значеннями однієї вибірки , ,..., та , ,…, є залежність, то маємо справу з автокореля-цією, якщо така залежність є між значеннями двох різних вибірок , ,..., та , ,..., , то це свідчить про наявність серійної кореляції. Автокореляція може бути як позитивною, так і негативною. Графічно ці випадки відображено в розділі 2, мал.2.6. Автокореляція може виникнути у зв'язку з інерційністю та циклічністю багатьох економічних процесів. Провокувати автокореляцію може і неправильно специфікована функціональна залежність у регресійних моделях та лагові запізнення в економічних процесах.

5.3.2. Тестування автокореляції

Найбільш відомим і поширеним тестом перевірки моделі на наявність кореляції між залишками є тест Дарбіна — Уотсона. На відміну від бага-тьох інших тестів, перевірка за тестом Дарбіна — Уотсона складається здекількох етапів і включає зони невизначеності.

Розглянемо порядок тестування за критерієм Дарбіна — Уотсона.

1. На першому етапі розраховується значення d-статистики за формулою:

У теорії доведено, що значення d-статистики Дарбіна — Уотсона знаходяться в межах від 0 до 4.

2. Задаємо рівень значимості та підраховуємо кількість факторів (к) у досліджуваній моделі. Припустимо к = р. За таблицею Дарбіна — Уотсона при заданому рівні значимості , кількості факторів к = р та кількості спостережень п, знаходимо два значення , та . Якщо розраховане значення d-статистики знаходиться в проміжку від 0 до , (0 < d < ), то це свідчить про наявність позитивної автокореляції. Якщо значення d потрапляє в зону невизначеності, тобто набуває значення d , або 4 - d 4 - , то ми не можемо зробити висновки ні про наявність, ні провідсутність автокореляції. Якщо 4 - < d 4, то маємо негативну автокореляцію. Нарешті, якщо < d < 4 - , то автокореляції немає. Всі ці випадки проілюстровано на мал. 5.7.

Малюнок 5.7. Зони автокореляційного зв'язку за критерієм Дарбіна — Уотсона

Розглянемо приклад. Припустимо, для певної простої регресійної моделі, яка має один фактор (к = 1), кількість спостережень дорівнює п = 20 та розраховане значення d-статистики дорівнює 0.34. Приймемо, що рівень значимості, тобто ризик відкинути правильну гіпотезу, дорівнює 5%. Затаблицею Дарбіна — Уотсона при к = 1 та п = 20 знаходимо = 1.20; = 1.41. Відповідно відкидаємо гіпотезу про відсутність автокореляції та приймаємо гіпотезу про наявність позитивної автокореляції.