7.8.6. Розподіл

Нехай ми маємо ряд нормально розподілених та незалежних змінних . Пронормуємо їх та отримаємо стандартні нормалізовані значення:

Сума квадратів нормалізованих величин розподіляється за розподілом із ступенями вільності, які дорівнюють ν:

де ν – кількість змінних, які ми сумуємо.

Функція густини розподілу зміщена праворуч відносно осі ординат, починається на початку координат та прямує до нескінченності. Із зростанням n функція густини стає дедалі асиметричнішою. Є спеціальна таблиця розподілу , яка є кумульованою: вона дає ймовірність того, що більше, ніж якесь значення при певних ступенях вільності та заданому рівні значимості.

Ми символічно можемо записати для оцінки , для якої 2,5% спостережень матимуть значення більше, ніж , тобто будуть знаходитися праворуч від на осі абсцис функції густини.

Так, для ступенів вільності 10 та рівня значимості 5% за таблицею знаходимо критичне значення 183, що можна записати:

P 18.3 < < = 0.05 (для 10).

Тобто ймовірність того, що > 183, дорівнюватиме 0.05 для 10 ступенів вільності.

7.8.7. T-розподіл Ст’юдента

Якщо змінна Z має стандартний нормальний розподіл з нульовим математичним сподіванням та дисперсією ; ~N(0,1), та інша незалежна змінна розподілена за розподілом з ν ступенями вільності, то число t=Z має t-розподіл з ступенями вільності.

Характеристики t-розподілу такі:

1. t-розподіл є розподілом, який має форму дзвона, симетричного відносно нульового значення (див. мал. 7.5);

2. значення t належать проміжку < t <+ ;

3. функція густини t-розподілу більш розтягнута, ніж функція нормального закону розподілу. Це означає, що площа на кінцях більша у t-розподілі, ніж у стандартному нормальному розподілі;

4. із збільшенням числа спостережень ( ) t-розподіл наближається до стандартного нормального розподілу. Відмітимо, якщо n>30, то t-розподіл Ст’юдента в нормальному законі розподілу;

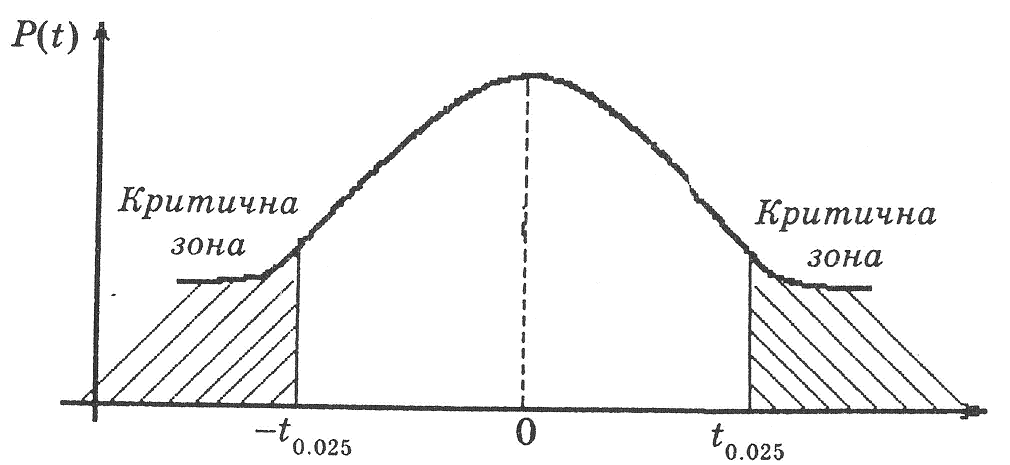
Малюнок 7.5. Функція густини t-розподілу Ст’юдента

5. t-розподіл залежить від ступеня вільності, тобто нам потрібно знайти ступені вільності, щоб отримати критичне значення з t-таблиці. Вона відрізняється від таблиці стандартного нормального розподілу тим, що включає ступені вільності. Таблиця перераховує значення t, з правої сторони якого ми знаходимо 10, 5, 2.5 та 0.5 відсотка площі під кривою. Символічно ми будемо записувати для оцінки t, праворуч – площа під кривою, яка становить 2.5%; для оцінки t, праворуч площа під кривою становить 1% від загальної суми і так далі. Наприклад, припустимо, ступені вільності дорівнюють 15 (df = 15). Ми можемо знайти з t-таблиці критичні значення t, які відповідають різним рівням значимості. Для рівня значимості 5% та df = 15 маємо: = 2.131.

Це можна розписати таким чином:

P 2.131 < t < 2.131 = 0.95 з 15 ступенями вільності.

Перетворення нормально розподіленої величини і її вибіркового середнього в t-величини віконується за допомогою формул:

та

Де - оцінка середнього квадратичного відхилення для малої вибірки (n<30).

,

де - оцінка дисперсії генеральної сукупності.

7.8.8. F-розподіл Фішера

Якщо дві змінні мають незалежні xi-квадрат розподіли i , відповідно з і ступенями вільності, тоді статистика

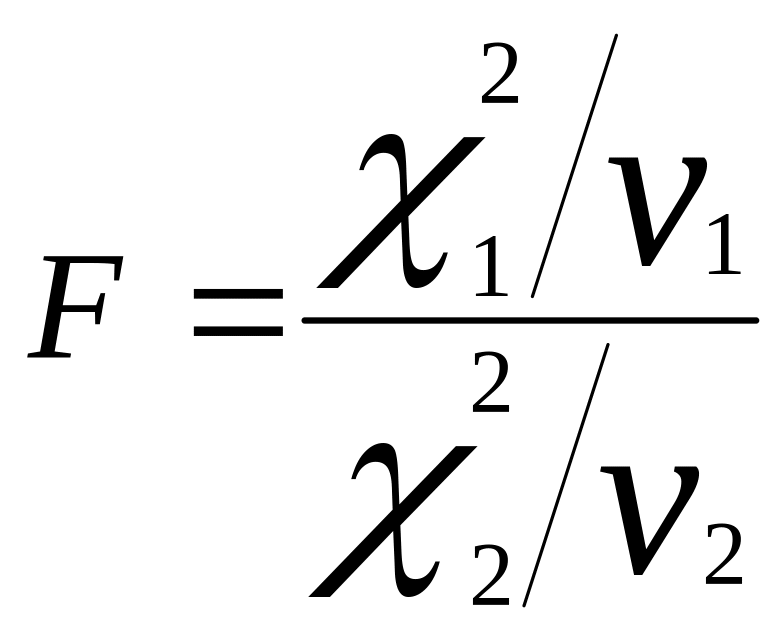
Має F-розподіл Фішера з і ступенями вільності.

F-статистику можна розглядати також як відношення двох незалежних оцінок дисперсій, і тому на практиці F-розподіл найчастіше вікористовується для тестування рівності цих оцінок дисперсій. З цієї причини F-статистику інколи назівають відношенням дисперсій:

= Відношення дисперсій

з і ступенями вільності.

Функція F-розподілу асиметрична (див.мал. 7.6).

Малюнок 7.6 Функція густини F-розподілу Фішера

Слід зазначити, що значення F-відношення завжди додатне і знаходиться в межах від нуля до плюс нескінченності (0 F + ). Значення F –відношення з різними ступенями вільності (і різними рівнями значимості) зведені в таблицю F-розподілу Фішера. Ступені вільності і залежать від оцінок дисперсій чисельника та знаменника F –відношення. F –таблиця дає критичні значення праворуч спрямованого хвоста. Якщо дві оцінки дисперсії близькі одна до одної, тоді відношення їх наближається до одиниці. Чим більша різниця між двома дисперсіями, тим більше значення F –відношення. Таким чином, загалом, великі значення F допускають, що різниця між двома оцінками є значною.

Розглянемо приклад перевірки на адекватність багатофакторної регресійної моделі з використанням F –критерію Фішера.

Нагадаємо, що при цьому ми формуємо нуль-гіпотезу рівності всіх параметрів багатофакторної регресії нулеві на противагу альтернативній гіпотезі, що хоча б один параметр не дорівнює нулю, тобто має місце регресійний зв`язок. При цьому нуль-гіпотеза має вігляд:

На противагу альтернативній гіпотезі, що

хоча б одне значення відмінне від нуля.

Якщо нуль-гіпотеза неправильна, то тоді правильна гіпотеза , тобто не всі параметри незначно відрізняються від нуля, що дає підставу вважати, що побудована регресійна модель відповідає дійсності, тобто адекватна. Для перевірки -гіпотези розраховується F-відношення Фішера з p та (n – p – 1) ступенями вільності:

де p – кількість факторів, які увійшли в модель; n – загальна кількість спостережень.

За F –таблицями Фішера, як і у випадку простої регресії, знаходимо критичне значення з p та (n – p – 1) ступенями вільності, задавши попередньо рівень значимості % (або рівень довіра (1- ) %).

Якщо F> , тоді нуль-гіпотеза відкидається, що свідчить про адекватість побудованої моделі. У протилежному віпадку вона приймається і модель вважається неадекватною.

ДОДАТКИ

ДОДАТОК 1