7.8.5. Нормальний закон розподілу

Числові характеристики неперервних випадкових величин

Нехай неперервна випадкова величина Х задана диференційною функцією Нехай усі можливі значення Х належать проміжку [a; b]. Розіб’ємо відрізок на n часткових відрізків довжиною і виберемо у кожному з них довільну точку

Математичні сподівання:

наближено дорівнює ймовірності влучення х в інтервалі .

Математичним сподіванням неперервної випадкової величини Х, можливі значення якої розташовані на відрізку [a, b], називають визначений інтеграл:

Якщо можливі значення належать усій осі, то

Дисперсія неперервної випадкової величини відповідно визначається за формулами:

Нормальним називають розподіл ймовірностей, який описується диференційною функцією виду:

де а – математичне сподівання, - середнє квадратичне відхилення випадкової величини.

Нормованим називають розподіл з а=0 і σ=1.

- нормована випадкова величина з M(t)=0, σ(t)=1.

.

Властивості функції густини нормального закону розподілу.

1. При х = а функція має максимум .

2. Графік функції є симетричним відносно прямої х = а.

3. Точки графіка

- точки перегину.

Малюнок 7.4. Функція густини нормального закону розподілу нормованої випадкової величини

7.8.5.1. Вплив параметрів нормального розподілу на форму нормальної кривої

Як бачимо з малюнка, функція густини нормального закону розподілу симетрична відносно свого математичного сподівання.

Із зростанням математичного сподівання а (на мал. 7.4. математичне сподівання дорівнює нулю) функція густини зсувається праворуч відносно осі х. Із спаданням а вона зсувається ліворуч.

Якщо зростає, крива стає більш похилою, тобто опускається до осі х; при зменшенні значення нормальна крива стає гостроверхою.

Будь-яку випадкову величину х, розподілену нормально з математичним сподіванням а та дисперсією , можна пронормувати, тобто звести до випадкової величини з математичним сподіванням нуль та дисперсією одиниця, шляхом такого перетворення:

, де х – випадкова величина;

а – математичне сподівання цієї випадкової величини;

- її середнє квадратичне відхилення .

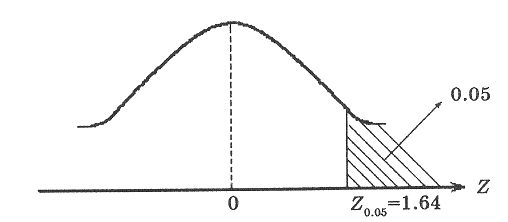
Для нормального закону розподілу 50% значень випадкової величини лежать у межах , 68% - у межах і 95% - у межах та 99,7% - у межах .

Щоб проілюструвати нормальний закон розподілу, розглянемо декілька прикладів.

Приклад 1. Показати, що при досить великій кількості класів (В) та при частоті кожного окремого значення змінна має нульове математичне сподівання (t=0) і дисперсію .

Розв’язок. За означенням математичного сподівання для дискретних випадкових величин маємо:

,

враховуючи, що

Дисперсія величини Т обчислюється за формулою:

.

Приклад 2. Нехай нам відомо, що надходження чеків до банку відповідає нормальному закону розподілу з математичним сподіванням х=5232 (грн..) та середнім квадратичним відхиленням σ =1972 (грн.). Нам потрібно знайти ймовірність надходження чека, вартість якого перебільшує 6000 (грн..). Формалізовано це можна записати таким чином:

Х – випадкова величина (вартість чеків);

Х – N (5232, 1972).

Треба знайти: Р ( Х > 6000) = ?

Розв’язок. Пронормуємо випадкову величину та знайдемо значення , яке відповідає .

Далі використаємо таблицю нормального розподілу. Враховуючи симетричність функції густини нормального закону розподілу, отримаємо ймовірність того, що буде дорівнювати Отже, імовірність того, що до банку надійде чек вартістю більше ніж 6000, дорівнює 0.3483. Тепер нас цікавить, імовірність того, що до банку надійде чек на суму меншу ніж 6000 (гривень). Оскільки ми вже маємо , то знайти дуже просто, знаючи, що . Отже, .

Але якби нам був невідомий попередній результат, ми б шукали цю імовірність аналогічно попередньому розрахунку. Справді, для нашого прикладу . З властивості того, що функція густини нормального закону розподілу симетрична відносно свого математичного сподіванні, випливає:

та .

Приклад 3. За умов прикладу 2 необхідно знайти ймовірність того, що до банку потрапить чек вартістю нижче ніж 4000 (гривень).

Розв’язок. Нормуючи випадкову величину х, отримаємо значення t:

звідки .

Приклад 4. За умов прикладу 2 визначимо імовірність того, що значення випадкової величини потрапить до інтервалу Наприклад, нас цікавить імовірність того, що вартість чека, який надходить, знаходиться у межах 4000 та 7000 (грн.). Нормування значення 4000 (грн.) та 7000 (грн. ) дасть нам:

Враховуючи ці межі, можна розписати:

За таблицею нормального закону розподілу, зробивши додаткові розрахунки, знаходимо та

Звідси маємо розв’язок: .

Звичайно, на практиці нас цікавить і протилежна проблема: як, знаючи ймовірність того, чи відбулася подія, встановити її значення. Це можна зробити, використавши таблицю нормального закону розподілу та провівши зворотні перетворення, що можна зобразити за допомогою схеми 1: