2.12.6. T-тест для оцінки значимості коефіцієнта кореляції
Ми знаємо, що коефіцієнт кореляції r вимірює щільність зв’язку між двома змінними. У випадку простої лінійної регресії він вимірює щільність зв’язку між незалежною змінною x і залежною змінною y. Задамося ціллю встановити:
як пов’язані коефіцієнт кореляції r між вибірковими значеннями x і y з коефіцієнтом кореляції ρ всієї генеральної сукупності;
як перевірити значимість коефіцієнта кореляції і як для цього використати t-статистику (2.115).
Спробуємо спочатку відповісти на друге запитання, що автоматично дає відповідь і на перше запитання. Використаємо t-статистику у вигляді (2.115) для визначення, чи статистично значимо коефіцієнт кореляції всієї сукупності відрізняється від нуля.
Спочатку розглянемо найпростіший випадок, а саме тест для оцінки значимості коефіцієнта кореляції (з припущенням, що ρ = 0).
Сформулюємо нуль-гіпотезу:
(2.116)
де r – вибірковий коефіцієнт кореляції між x і y;
n – кількість спостережень.
Величина t* розподілена за розподілом Ст’юдента з (n-k) ступенями вільності (нагадаємо, що для простої лінійної регресії k = 2).
Розраховане
значення t*
порівнюємо з критичним значенням
при
α 100%-ному
рівні значимості й (n-2)
ступенях вільності. Якщо
,
відкидаємо нуль-гіпотезу
і
приймаємо гіпотезу
.
Приклад. Маємо вибірку значень x і y, яка складається з 20 спостережень; коефіцієнт кореляції r = 0,82. Ми хочемо перевірити при 5%-ному рівні значимості, чи значимо коефіцієнт кореляції відрізняється від нуля.
Тобто перевіряємо нуль-гіпотезу:
проти альтернативної:
.
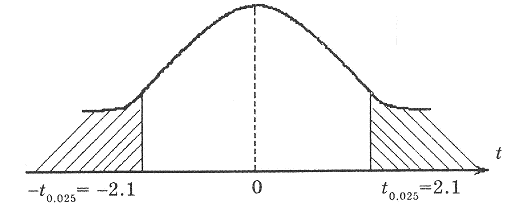
Малюнок 2.14. Перевірка на значимість коефіцієнта кореляції за t-тестом Ст’юдента
За
t-таблицями
Ст’юдента знаходимо теоретичне значення
t з 18
ступенями вільності і 5%-ним рівнем
значимості, яке дорівнює
(мал. 2.14). Оскільки t*>t,
ми відкидаємо нуль-гіпотезу і робимо
висновок, що
.
Трансформований у z-тест t-тест для оцінки значимості коефіцієнта кореляції (з припущенням, що )
Якщо
,
то t-розподіл
з коефіцієнтом ρ
є несиметричним. Тобто
t-статистику
не можна використовувати для перевірки
таких гіпотез, як
або
.
Цю проблему було вирішено в 1921 році Фішером, який трансформував ρ у величину h:
,
розподілену нормально з математичним сподіванням
і дисперсією
що формалізовано можна записати
.
Як будь-яку нормально розподілену величину, її можна стандартизувати, тобто звести до нормально розподіленої величини з математичним сподіванням 0 і дисперсією 1 шляхом перетворення:
Приклад. З вибірки, що складається з 28 спостережень, знайдено, що r = 0.70.
Чи варто відкинути гіпотезу, що ρ = 0.6 ( в генеральній сукупності) з ризиком помилитися 5%?
Тобто перевіряємо нуль-гіпотезу:
проти
Для цього обчислимо величину:
Далі розрахуємо значення z-статистики:
З
огляду на те, що заданий рівень помилки
α=0.05, за таблицями нормального розподілу
знаходимо критичне значення
Табличне
значення
(мал. 2.15).
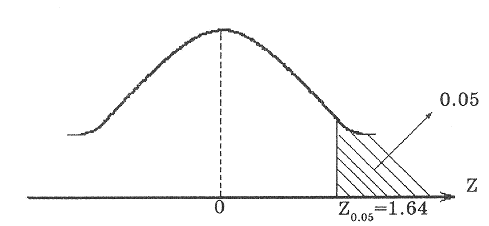
Малюнок 2.15. Функція густини нормального закону розподілу