1.2. Практичні наслідки мультиколінеарності

а) велика дисперсія і коваріація оцінок параметрів, обчислених за МНК;

Наприклад, з виразів для розрахунку дисперсій та коефіцієнта коваріації між параметрами 1 і 2 для двохфакторної моделі витікає, що при збільшенні коефіцієнта кореляції між параметрами х₁ і х₂, вони нелінійно зростають. швидкість зростання збільшується при наближенні коефіцієнта кореляції до свого граничного значення 1.

var(b₁) cov(b₁,b₂)

p D

0.67D

0 1 r_x1,x2 0 0.5 0.9 1 r_x1,x2

б) збільшення інтервалів довіри.

Оскільки збільшуються середні квадратичні відхилення, то збільшуються інтервали довіри параметрів.

в) незначимість t-статистики.

Оскільки ця статистика зворотньо пропорційна середньому квадратичному відхиленню, яке нескінченно зростає, то її значення прямує до нуля.

Якщо єдиною метою регресійного аналізу є прогноз, то мультиколінеарність не становить проблеми, коли значення залежних змінних мають однакову майже лінійну залежність с початковою матрицею Х, оскільки чим вище значення коефіцієнта детермінації, тим точніший прогноз. Тобто, якщо у побудованій регресії встановлено, що приблизно х₁=2х₂, то у прикладах прогнозу це співвідношення повинно зберігатися, що буває дуже нечасто.

Якщо метою аналізу є дійсні значення параметрів, то мультиколінеарність стає проблемою, оскільки зростають стандартні помилки в оцінці параметрів.

1.3 Тестування наявності мультиколінеарності

Єдиного методу тестування наявності мультиколінеарності не існує. Розглянемо кілька методів.

а) Високе значення R² та незначимість t-статистики.

Одночасна наявність цих двох факторів є “класичною” ознакою мультиколінеарності.

За тестом Ст`юдента можна виявити, що один або більше оцінених параметрів статистично незначимо відрізняються від нуля. При високому рівні R² ми приймаємо з великим ступенем ймовірності F-критерій Фішера, бо він відкидає нульову гіпотезу, коли ₁=₂=...=_p=0. Тому одночасна наявність цих двох факторів може свідчити про наявність мультиколінеарності.

б) Високе значення парних коефіцієнтів кореляції.

Ця умова є достатньою, але не необхідною умовою наявності мультиколінеарності.

Якщо значення хоча б одного коефіцієнта кореляції більша за 0.8, то мультиколінеарність є серйозною проблемою.

в) F-тест.

Цей тест було запропоновано Глаубером і Фарром і полягає в тому, що для визначення щільності регресійного зв`язку будується регресійна залежність кожного фактора х_і з усіма іншими факторами і обчислюється коефіцієнт детермінації для цього допоміжного регресійного рівняння. Тому цей тест має ще назву “побудова допоміжної регресії”. Наприклад, коефіцієнт детермінації R²_{x2x1x3,...,xp} відповідає регресії x₂=b₀+b₁x₁+b₃x₃+...+b_px_p+e.

Для кожного коефіцієнта детермінації розраховуємо F_і-відношення

де n - кількість спостережень; р - кількість факторів.

F-тест перевіряє гіпотезу Н₀: R²_{xіx1x2,...,xp} =0 проти альтернативної Н₁: R²_{xіx1x2,...,xp} 0.

Розраховані значення порівнюємо з критичним F, знайденим з (р-1) і (n-р) ступенями вільності і заданим рівнем значимості. Якщо F_і>F_кр, тоді ми відкидаємо 0-гіпотезу і вважаємо, що фактор х_і є мультиколінеарним, а в іншому випадку впевнюємося, що він не є мультиколінеарним.

г) Характеристичні значення та умовний індекс.

Цей тест за допомогою апарату матриць у деяких програмах обчислює умовне число k

k=(максимальне характеристичне значення)/(мінімальне характеристичне значення)

і умовний індекс (СІ)

СІ=

Якщо 100k1000 або 10CI30, то мультиколінеарність помірна, при k>1000 або CI>0 - висока.

----------------------------------------------------------------------------------

Тестування наявності гетероскедастичності

Інколи наявність гетероскедастичності вгадується інтуітивно або висувається як припущення. Наприклад, при вивченні бюджету сім`ї можна помітити, що дисперсія залишків зростає, або при вивченні діяльності різних за розмірами фірм можна очікувати гетероскедастичність. Як і випадку мультиколінеарності, єдиних правил виявлення гетероскедастичності немає. Розглянемо найпростіші тести.

а) графічний аналіз. Це простий і наочний метод. Спочатку роблять аналіз моделі на основі припущення про гомоскедастичність, а потім будують графіки залежності квадратів залишків від залежної змінної і з`ясовують, чи оцінене середнє значення у систематично пов`язане з квадратом залишків. Звичайно квадрати залишків, отримані з вибіркової моделі є лише оцінками невідомих квадратів залишків генеральної сукупності, але, особливо при великих вибірках, вони можуть успішно використовуватись.

e² e²

y(x) y(x)

лінійна

e² e²

y(x) y(x)

квадратична

Цей метод дозволяє проаналізувати залежність не тільки між у та квадратами залишків, а й між будь-якою незалежною змінною і квадратами залишків. Графічний аналіз дозволяє не тільки виявити наявність гетероскедастичності, а й зробити висновок про форму зв`язку, що потрібно при трансформації наявних даних для побудови моделі з гомоскедастичністю помилок.

б) тест рангової кореляції Спірмана.

Це найпостіший тест, який можна використовувати як до малих, так і до великих вибірок.

Коефіцієнт рангової кореляції Спірмана

(5.41)

де d_i - різниця між рангами, що приписуються двом характеристикам і-го об`єкта; n - кількість об`єктів, що ранжуються.

Наприклад y_i=₀+₁x_i+_i

Етап 1. Побудувати регресію для даних х та у і розрахувати відхилення.

Етап 2. Проранжувати абсолютні значення e_i та x_i у зростаючому чи спадному порядку і підрахувати коефіцієнт рангової кореляції Спірмана за (5.41).

Етап 3. Перевірити значимість отриманого коефіцієнта за t-тестом Ст`юдента, тобто побудувати t-статистику

t=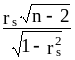 (5.42)

де n - кількість спостережень та df=(n-2) - кількість ступенів вільності. За таблицями знайти для заданого рівня значимості t_кр. Якщо t>t_кр, то це підтверджує гіпотезу про гетероскедастичність, а якщо t<t_кр, тоді в регресійній моділь є правильним припущення про гомоскедастичність.

б) тест Голдфелда та Квондта.

Цей тест застосовується для великих вибірок. Спостережень має бути хоча б удвоє більше, ніж оцінюваних параметрів. Тест припускає нормальний розподіл та незалежність величини _i.

Нульовою гіпотезою для цього теста є H₀: _i - гомоскедастична, а альтернативною H₁: _i - гетероскедастична.

Етап 1. Ранжуємо спостереження незалежної змінної в порядку зростання або спаду значень. У випадку багатофакторної регресії проводимо ранжування за однією вибраною незалежною змінною (якщо апріорі важко визначити змінну для ранжування, то послідовно застосовуємо тест до кожної змінної).

Етап 2. Задаємо кількість с центральних спостережень, які ми будемо виключати з подальшого аналізу. Для n>30 оптимальне с становить приблизно чверть усіх спостережень(для n=30 с=8, для n=60 с=16). Залишок спостережень (n-с) ділиться на дві однакові підвибірки (n-c)/2, одна з яких включає великі значення х, а друга - малі.

Етап 3. Будуємо окрему регресію для кожної вибірки і розраховуємо суми квадратів залишків e₁²- для підвибірки з малими значеннями х, e₂²- для підвибірки з великими значеннями х. Кожна сума квадратів має [(n-c)/2]-k ступенів вільності, де k - загальна кількість оцінюваних параметрів у моделі.

Якщо кожну з цих сум поділити на кількість ступенів вільності, то отримаємо оцінки дисперсії випадкової величини  в двох підвибірках. Відношення двох дисперсій

має F-розподіл (із ₁=_=[(n-c)/2]-k=[(n-c-2k)/2] ступенями вільності, де k - кількість оцінюваних параметрів з кожної регресії.

Якщо дві дисперсії рівні (випадок гомоскедастичності), то розраховане відношення дорівнюватиме 1. Якщо наявна гетероскедастичність, тоді, оскільки за умовами тесту e₂²>e₁², F* буде більшим. Розраховане значення F* порівнюється з F_кр із ₁=_=[(n-c- 2k)/2], знайденим за таблицями, що відповідає значенням, які б мало F, якби справджувалася гіпотеза про гомоскедастичність. Якщо F*> Fкр, то ми відкидаємо гіпотезу про гомоскедастичність, тобто констатуємо наявність гетероскедастичності, а якщо F*<F, то приймаєму нульову гіпотезу. Чим більше F*, тим більша гетероскедастичність .

в) тест Глейзера (розглянемо на прикладі простої лінійної регресії).

Етап 1. Знаходимо параметри простої лінійної регресії за МНК та обчислюємо помилки для кожного спостереження. (Для багатофакторної регресії знаходимо помилки для моделі з усіма факторами.)

Етап 2. Будуємо регресію, яка пов`язує абсолютні значення помилок з незалежною змінною х. Оскільки ex=0, то, якщо брати справжні значення помилок, не можливо буде побудувати регресію e=f(x). Фактична форма цієї регресії невідома, тому для неї можна підбирати різні форми кривих, наприклад

e_i=₀+₁x_i²+u_i,

e_i=₀+₁x_i^-1+u_i,

e_i=₀+₁x_i^1/2+u_i,

e_i= +u_i,

e_i= +u_i.

Обираємо ту регресію, яка найкраще підходить з огляду на коефіцієнт кореляції та середні квадратичні відхилення параметрів b₀ та b₁. (Зверніть увагу, що коли b₀=0 та b₁0, така ситуація називається “чиста гетероскедастичність”, якщо b₀0 та b₁0, то цей випадок називається “змішана гетероскедастичність”. За цим тестом ми перевіряємо на значимість параметри b₀ та b₁, і якщо вони значимо відрізняються від нуля, то наявна гетероскедастичність.

Для багатофакторної регресії на цьому етапі будуємо залежність між абсолютними величинами знайдених помилок та залежною змінною у.

Перевага тесту Гейзера полягає в тому, що він дає також інформацію про форму залежності між ²_i та x_i, що потрібно для виправлення гетероскедастичності. Для визначення гетероскедастичності звичайно віддають перевагу тестам рангової кореляції Спірмана і Голдфелда та Квондта, а потім, якщо якимось з цих тестів виявлена гетероскедастичність, працюють з функцією Глейзера (e_i=f(x)) з метою вирішення, які зміни початкових даних необхідні, щоб подолати гетероскедастичність.

Вилучення гетероскедастичнсті

Після того, як встановлена наявність гетероскедастичності для її вилучення потрібно змінити модель таким чином, щоб помилки мали постійну дисперсію. Далі параметри трансформованої моделі розраховуються за МНК. Трансформація моделі полягає у зміні її первісної форми і залежить від форми залежності між дисперсією та значеннями незалежних змінних.

Коли гетероскедастичність має вигляд

E(e_i)²=²_i =k²f(x_i),

де k - скінченна константа; f(x_i) - функція від x_i, то трансформація початкової моделі здійснюєть шляхом її ділення на .

Така трансформація еквівалентна застосуванню методу зважених найменших квадратів (МЗНК), який є особливим випадком МУЗК.

За МНК ми мінімізуємо просту функцію квадратів відхилень, у якій кожне відхилення має однакову вагу (сума ваг=1) і є оцінкою відхилень генеральної сукупності. Якщо дисперсія відхилень не є сталою, то більша дисперсія дає менш точну вказівку на те, де проходить правильна регресійна лінія. Тому у підборі лінії регресії доцільно надавати меншу увагу спостереженням з більшою дисперсією відхилень порівняно з іншими спостереженнями. Цього можна досягнути наданням різної ваги кожній помилці генеральної сукупності чи її оцінці. Інколи доцільно поділити кожне відхилення на дисперсію випадкової величини, що відповідає наданню малих ваг великим помилкам, і мінімізувати зважену суму квадратів відхилень.

Такий метод і називається МЗНК. Прирівнявши часткові похідні зваженої суми до нуля і розв`язавши систему рівнянь, ми знаходимо формули для знаходження невідомих параметрів b₀ і b₁, що можливо при відомій дисперсії ²_i. Але на практиці ця дисперсія може бути невідомою, в такому випадку наведена вище трансформація початкової моделі аналогічна застосуванню МЗНК для початкової моделі. Мінімізація зваженої суми квадратів відхилень виводить аналогічні формули для оцінок параметрів початкової моделі, як і застосування простого МНК до трансформованої моделі.

Наприклад,

²_i =k²x_i², (1)

тому трансформована модель у_i/x_i=b₀/x_i+b₁+_i/x_i має гомоскедастичне відхилення з дисперсією k². МНК щодо трансформованої моделі полягяє в знаходженні таких значень невідомих параметрів b₀ та b₁, при яких мінімальна сума квадратів відхилень

Ефективність оцінок трансформованої моделі

Оцінки трансформованої моделі мають меншу дисперсію (є ефективнішими), ніж оцінки, отримані із застосуванням МНК до початкової моделі.

Для початкової гетероскедастичної моделі y_i=₀+ ₁x_i+_i з гетероскедастичністю за формулою (1) дисперсія параметра b₁

var(b₁)= .

Для трансформованої версії початкової моделі

y_i/x_i =₀/x_i + ₁+_i,

де _i =_i/x_i із сталою дисперсією k²

.

Слід звернути увагу, по-перше, на те, що гетероскедастичність може траплятися через невраховані змінні, тобто через погану специфікацію моделі. Тоді введенням цих змінних у модель можливо позбутися гетероскедастичность. Сліпе застосування трансформації, наведеної вище, зробить гомоскедастичною випадкову змінну, але оцінки параметрів можуть залишитися неправильними через неврахування важливих факторів. Наприклад, у функції заощаджень гетероскедастичність може виникати через зміни в економічній політиці (податкові реформи, знецінення національної валюти). У цьому випадку рішенням буде врахування у функції певних факторів, які б відбивали зміни в політиці уряду.

По-друге, у своїх діях ми припускали, що випадкова змінна розподілена нормально, що необхідно для перевірки на значимість оцінок параметрів за статистичними тестами та побудови інтервалів довіри. Якщо це припущення порушується, то оцінки залишаються найкращими, але за класичними тестами ми не зможемо визначити їх статистичну надійність, бо вони базуються на нормальному законі розподілу. Однак, з практики відомо, що інші закони розподілу досить добре апроксимуються нормальним законом, якщо розмір вибірки становить хоча б 10-20 спостережень, хоча за центральною граничною теоремою він повинен прямувати до нескінченності.

Автокореляція

Автокореляція або серійна кореляція має місце, коли порушується припущення класичного регресійного аналізу про незалежність випадкових величин, тобто E(_і_j)0, іj.

Автокореляцією називається залежність між значеннями однієї вибірки з запізненням на один лаг. Автокореляція може бути позитивною і негативною. Автокореляція може виникнути внаслідок інерційності та циклічності багатьох економічних процесів, неправильної специфікації функціональної залежності у моделі та лагових запізнень у економічних процесах.

Серійною кореляцією називається залежність між значеннями двох різних вибірок.

Тестування автокореляції

Найбільш поширеним тестом є тест Дарбіна-Уотсона, який складається з декількох етапів.

Етап 1. Розраховується значення d-статистики

Доведено, що значення d-статистики знаходиться в межах від 0 до 4.

Етап 2. Для заданого рівня значимості , кількість факторів k та кількості спостережень n за таблицею Дарбіна-Уотсона знаходимо два значення d_L, d_U. Якщо

0<d<d_L - наявна позитивна автокореляція;

d_Ldd_U або 4-d_Ud4-d_L - зона невизначеності (ми не можемо зробити висновків);

4-d_L<d<4 - негативна автокореляція;

d_U<d<4-d_U- автокореляція відсутня.

Позитивна Зона Відсутня Зона Негативна

0 d_L d_U 2 4-d_U 4-d_L 4

Оцінка параметрів моделі при наявності автокореляції

МНК в умовах автокореляції призводить до таких наслідків:

а) оцінки пармаметрів, залишаючись лінійними і незміщеними, не матимуть найменшу дисперсію, тобто не будуть BLUE-оцінками

б) оцінка дисперсії випадкової величини часто переоцінює дійсну дисперсію, тобто ми матимемо переоцінений коефіцієнт детермінації;

в) дисперсія параметрів моделі породжує помилки при використанні t- та F-тестів.

При наявності автокореляції слід користуватися для оцінки невідомих параметрів МУНК.

Видача завдань на курсове проектування, консультування щодо виконання задач курсового проекту та захист курсового проекту відбувається за рахунок аудиторних занять з індивідуальної роботи. При необхідності можуть бути організовані додаткові консультації.

Виконання курсового проекту відбувається за рахунок індивідуальної роботи та самостійної роботи студентів.