2. Задача о четырех красках.

Формулировка этой задачи чрезвычайно проста и не соответствует всей глубине и сложности проблемы: можно ли на любой политико-административной карте раскрасить страны так, чтобы никакие две страны, имеющие общую границу, не были раскрашены одинаковой краской, и чтобы были использованы всего четыре краски? Уточним, что если две страны граничат по точке, то они не считаются имеющими общую границу.

В терминах теории графов задача может быть поставлена следующим образом. Дан произвольный полностью неориентированный плоский граф . Можно ли каждую вершину графа раскрасить с помощью одной из четырех красок так, чтобы никакие две смежные вершины (вершины, соединенные хотя бы одним ребром) не были раскрашены в один цвет. Конечно, нетрудно привести примеры графов, которые раскрашиваются в одну, две, три или четыре краски. В §6 будет доказана теорема о том, что любой плоский граф может быть раскрашен с помощью пяти красок. Тем не менее, проблема четырех красок до сих пор не решена. Удалось лишь доказать, что такую раскраску можно осуществить для всех плоских графов с числом вершин, не превосходящим 38.

Задача эта приобрела известность с 1878 г., когда английский математик Кэли привел ее формулировку на заседании английского королевского научного общества; добавив, что не мог ее решить, хотя и размышлял над ней длительное время. С тех пор многие выдающиеся математики пробовали свои силы в решении этой задачи. Удивительно, что для графов, нарисованных на торе, листе Мёбиуса или бутылке Клейна, соответствующая задача решена, т. е. установлено необходимое и достаточное число красок для раскрашивания.

§3. Алгоритмические задачи.

1. Задачи о кратчайших путях.

1. Путь с наименьшим числом дуг. Пусть задан произвольный граф . Требуется построить такой путь, соединяющий две заданные вершины и , который содержит наименьшее число дуг (путь кратчайшей длины, если считать, что длины всех дуг одинаковы).

Если граф содержит небольшое число вершин и дуг, а задачу решает человек, то искомый путь может быть непосредственно «увиден», т. е. найден без применения каких-либо явно осознаваемых правил. При значительном количестве вершин и дуг в графе возникает необходимость в четком описании способа решения задачи.

Алгоритм решения.

1°. Присвоить вершине метку 0.

2°. Если и , то присвоить каждой такой вершине метку 1.

3°. Пусть — множество вершин, имеющих метку . Вершинам множества при присвоить метку .

4°. Процесс присвоения вершинам меток прекратить, как только вершина получит некоторую метку .

5°. Рассмотреть вершины , такие, что

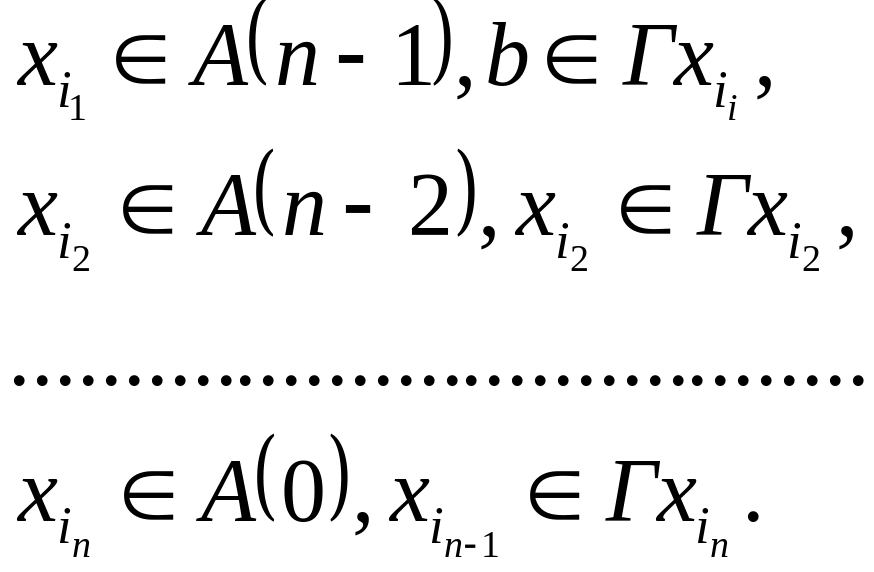
Замечание: Если на некотором шаге невозможно присвоение метки от значения вершинам в силу того, что множество пусто, и вершина не получила метки, то это означает, что в графе не существует никакого пути, соединяющего вершину с вершиной .

Доказательство того, что применение правил алгоритма всегда приводит к решению задачи 1, основывается на том очевидном факте, что вершины множества — это все те вершины, в которые можно попасть из вершины по путям, содержащим ровно дуг, и нельзя попасть по пути длины меньшей, чем .

2. Путь кратчайшей длины. Рассмотрим теперь случай, когда каждой дуге графа сопоставлено положительное число . Это число можно назвать длиной дуги. Длиной пути назовем сумму длин дуг, входящих в путь :