4. Исходные данные к контрольной работе

4.1. Условия задач

Задача 1. Расчет бруса круглого поперечного сечения на изгиб с кручением

На стальной вал постоянного сечения диаметром d, вращающийся со скоростью n об/мин, через ведущий шкив «I» с помощью ременной передачи передается мощность P кВт, которая затем распределяется между ведомыми шестернями «2» и «3» в заданном отношении.

При расчете массами шкива и шестерен пренебречь.

Натяжение ведущей ветви ремня F₁ принято равным удвоенному натяжению ведомой ветви t₁(F₁=2t₁).

Длина a=10 см. Допускаемое напряжение  = 160 МПа.

Требуется:

1. Определить нагрузки, действующие на вал, т.е. скручивающие моменты и силы в местах посадки шкивов и шестерен.

2. Силы, действующие на вал, разложить на составляющие в вертикальной и горизонтальной плоскостях.

3. Построить эпюру крутящих моментов.

4. Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях.

5. Построить эпюру суммарных изгибающих моментов.

6. Найти опасное сечение и вычислить в этом сечении значение эквивалентного момента.

7. Определить диаметр вала, округлив его до стандартных размеров (мм): 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 170, 180, 200.

Задача 2. Расчёт плоской статически неопределимой рамы методом сил

Плоская статически неопределимая рама загружена распределённой нагрузкой интенсивностью q, сосредоточенной силой F и сосредоточенным моментом M.

Требуется:

1. Определить степень статической неопределимости.

2. Выбрать основную статически определимую систему путем отбрасывания в заданной системе лишних связей.

3. Действие отброшенных связей возместить приложением к основной системе неизвестных усилий.

4. Составить канонические уравнения, которые показывают, что полные перемещения в основной системе, возникающие по направлениям неизвестных усилий под влиянием этих усилий и заданной нагрузки, равны нулю.

5. Нагрузить основную систему поочередно единичными усилиями 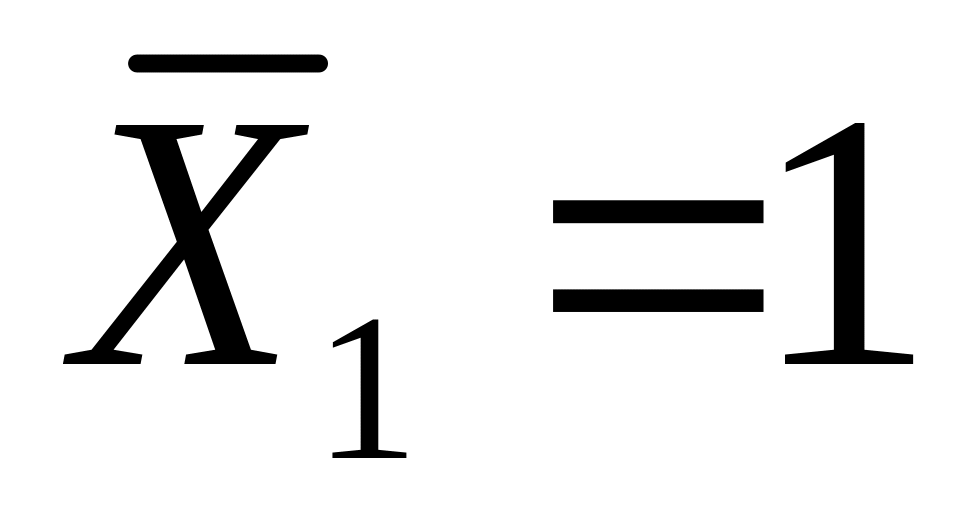, 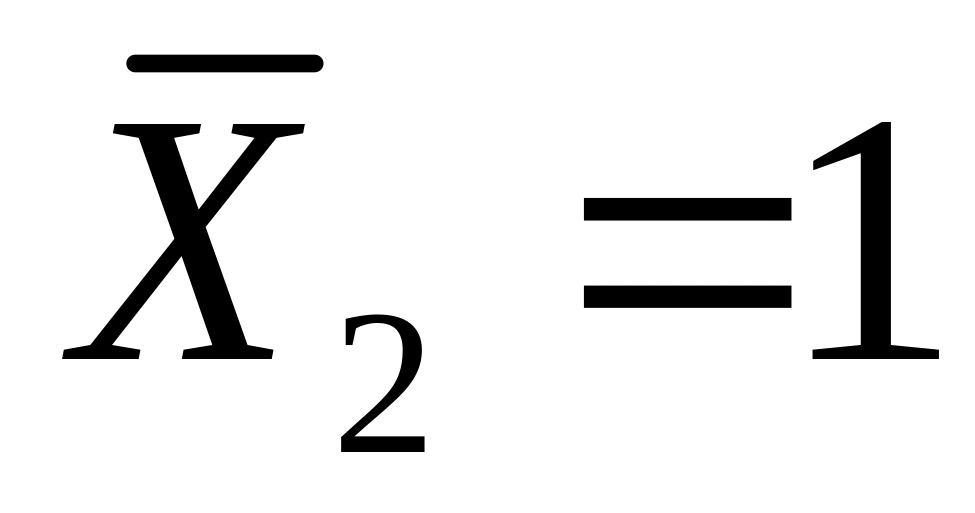и от каждого из них отдельно построить единичные эпюры изгибающих моментов , и грузовую эпюру изгибающих моментов 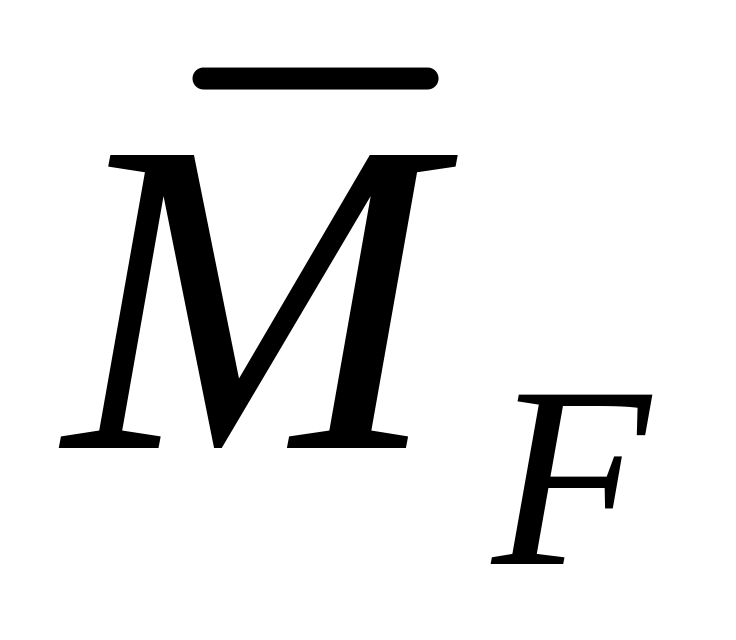от внешних нагрузок.

6. Вычислить все коэффициенты системы канонических уравнений путем перемножения единичных эпюр.

7. Определить грузовые члены системы канонических уравнений путем перемножения единичных эпюр с грузовой эпюрой.

8. Нагрузить основную систему одновременно единичными усилиями , и построить от них суммарную единичную эпюру изгибающих моментов .

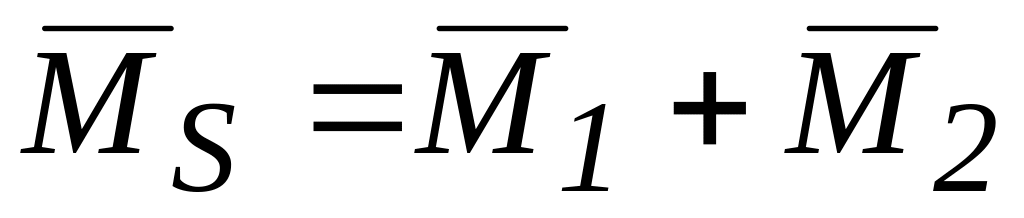9. Вычислить коэффициент 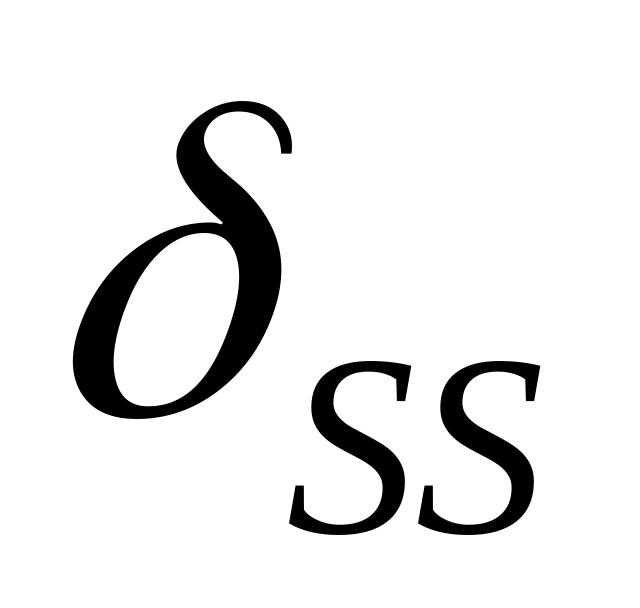путем перемножения суммарной эпюры 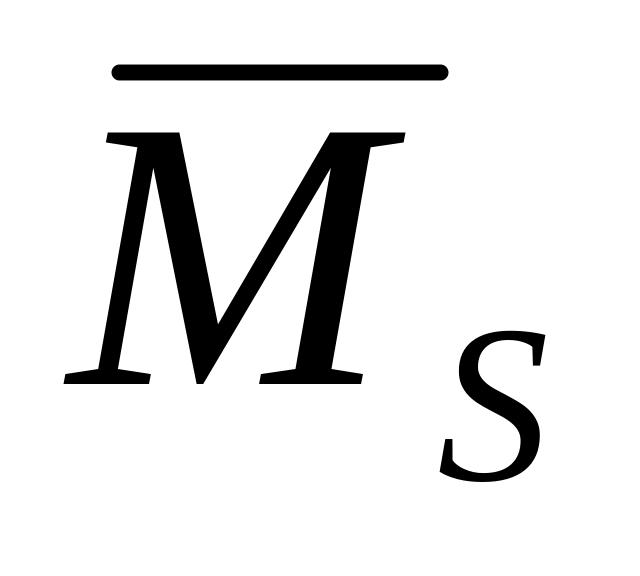саму на себя.

10. Определить грузовой член 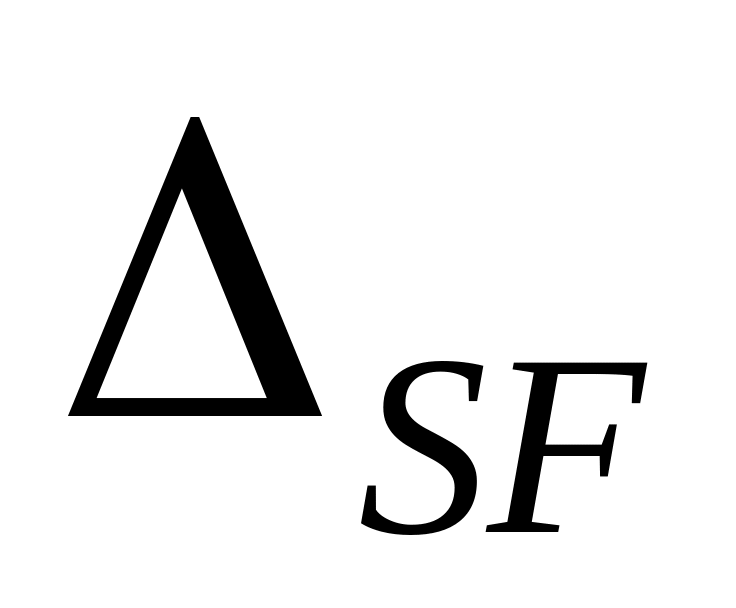путем перемножения суммарной эпюры 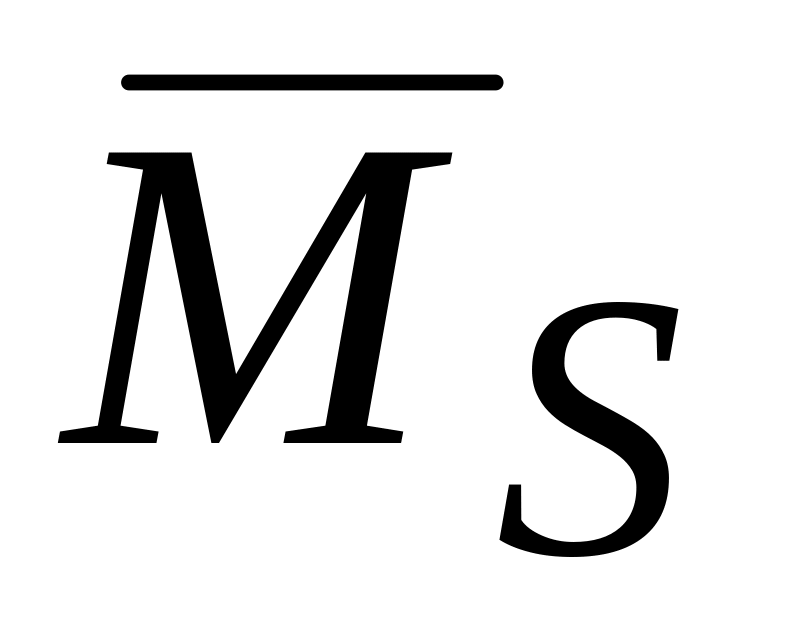с грузовой эпюрой.

11. Выполнить универсальную проверку нахождения коэффициентов 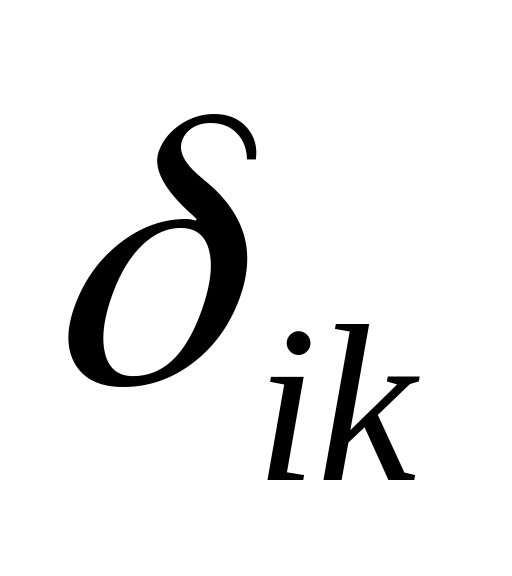и грузовых членов .

12. Решить систему канонических уравнений, в результате чего найти значения неизвестных , .

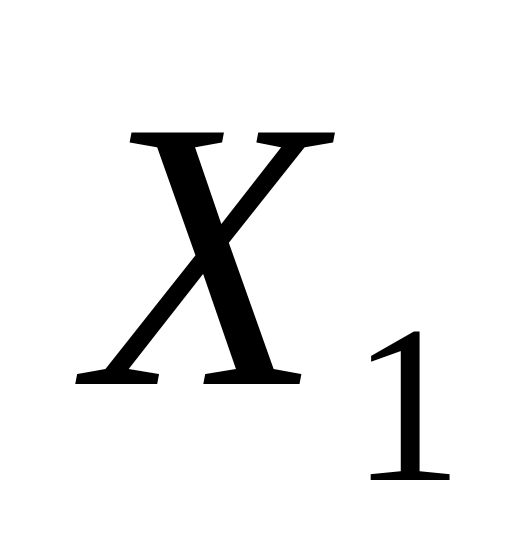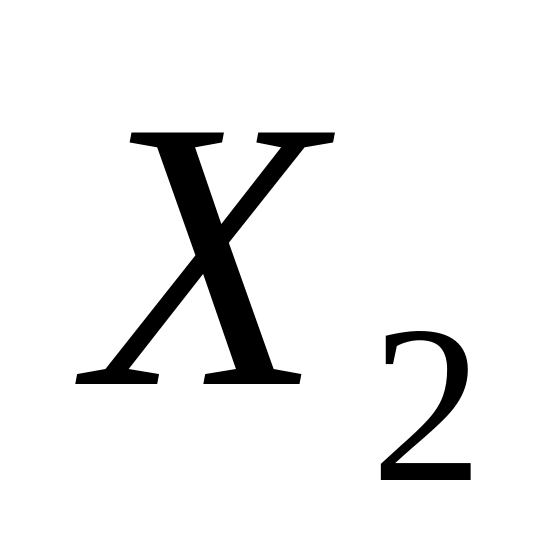13. Построить для рамы эпюру изгибающих моментов, нагрузив ее заданными нагрузками и найденными неизвестными , (построение эпюры изгибающих моментов можно выполнить с использованием формулы: ).

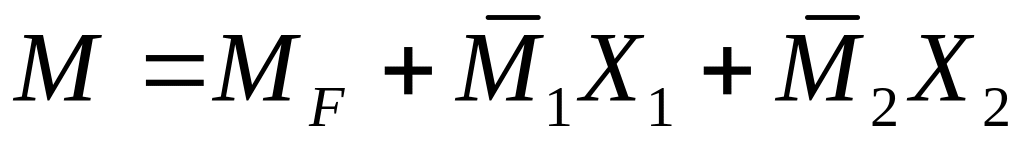14. Выполнить деформационную проверку правильности нахождения неизвестных усилий , .

15. Построить для рамы эпюры поперечных и продольных сил.

16. Для узлов и всей рамы выполнить статическую проверку.

Задача 3. Расчет сжатого бруса на устойчивость

Стальная стойка длиной l нагружена продольной сжимающей нагрузкой F. Допускаемое напряжение на сжатие _с = 160 МПа, модуль упругости материала E=2∙10¹¹ Па.

Требуется:

1. Подобрать размеры поперечного сечения круглой и составной стоек.

2. Сравнить полученные стойки по расходу материала и принять наиболее рациональную.

3. Определить критическую силу для принятой стойки.

4. Найти коэффициент запаса устойчивости.