3. Расчет прямолинейной сжатой стойки на устойчивость

3.1. Краткие теоретические сведения

Если стойку с прямолинейной осью последовательно нагружать все возрастающей продольной нагрузкой, то при некотором ее значении стойка будет иметь две формы равновесия: прямолинейную неустойчивую и криволинейную устойчивую.

Явление изгиба стойки при приложении к ней продольной силы носит название потери устойчивости. Минимальное значение сжимающей силы, при которой ось стойки может иметь устойчивую криволинейную и неустойчивую прямолинейную форму упругого равновесия, называется критической силой. Опасность явления потери устойчивости состоит в том, что оно может наступить внезапно при значении напряжения существенно меньшего, чем предел прочности материала стойки. Поэтому сжатый стержень помимо условия прочности должен удовлетворять условию устойчивости:

,

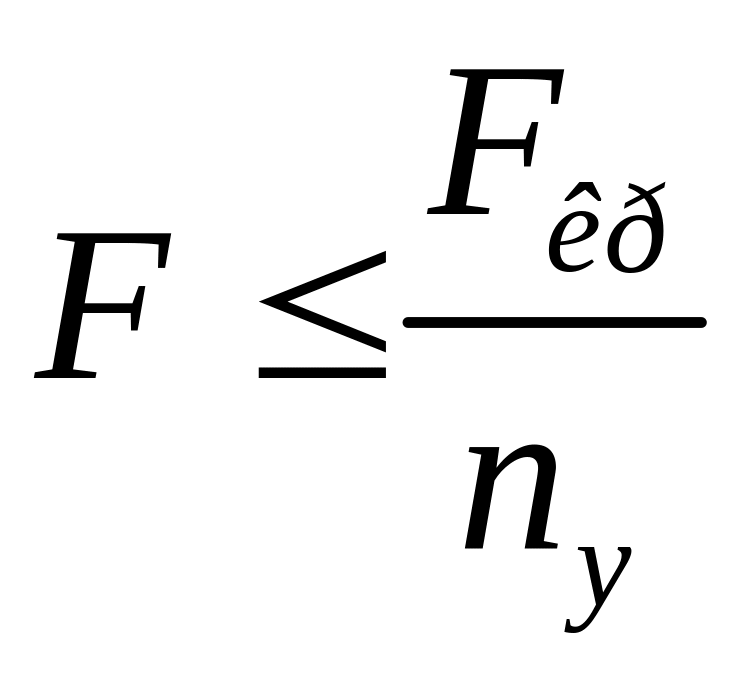где F – значение силы, сжимающей стержень; F_кр – значение критической для заданного стержня силы; n_у – нормативный коэффициент запаса устойчивости.

Величина F_кр для длинных стержней с различными опорными устройствами определяется по формуле Эйлера:

,

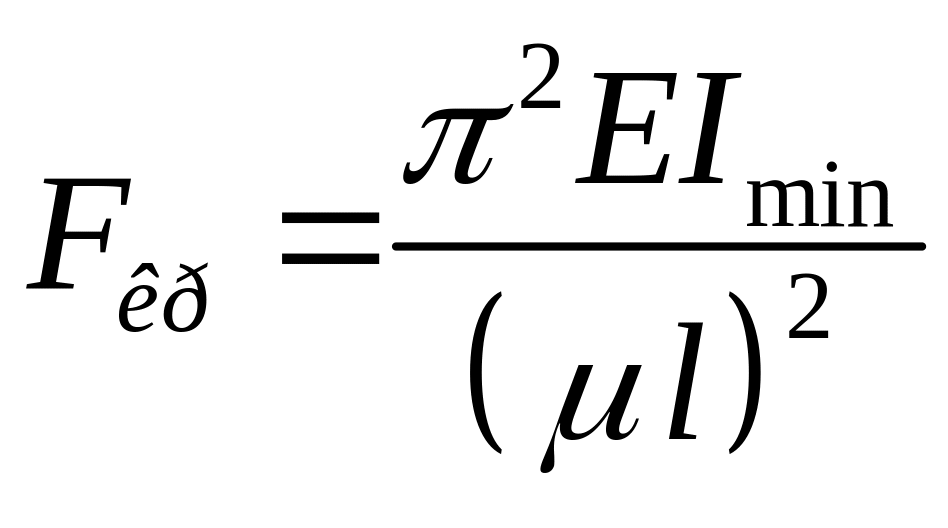где - наименьший момент инерции поперечного сечения стойки; - длина стойки; - коэффициент приведения длины балки, учитывающий условия ее закрепления относительно оси с .

Если F_кр определить по формуле Эйлера, то формула критического напряжения имеет вид:

,

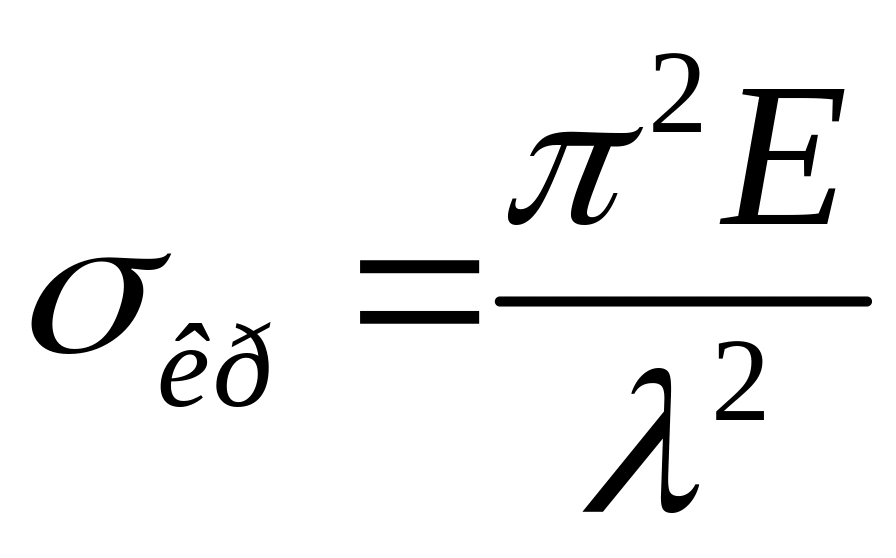где 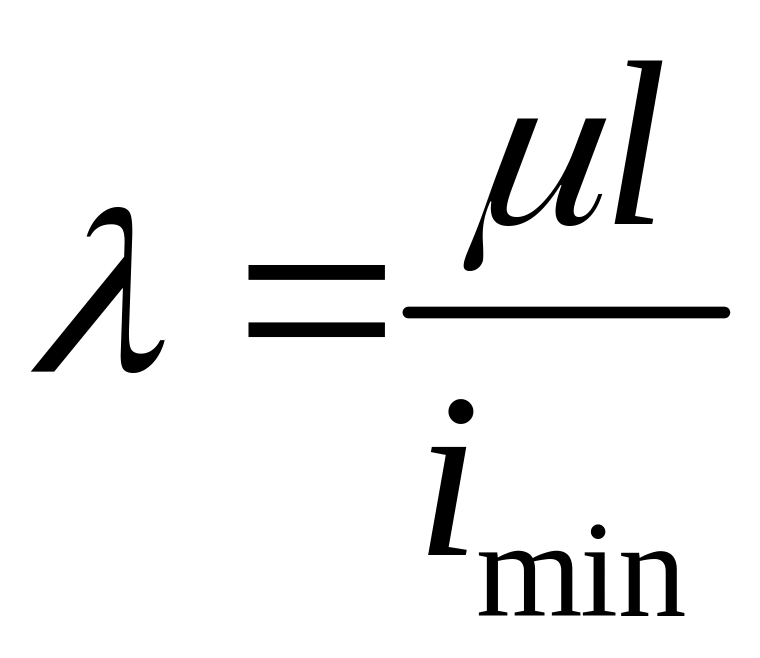- гибкость стойки; 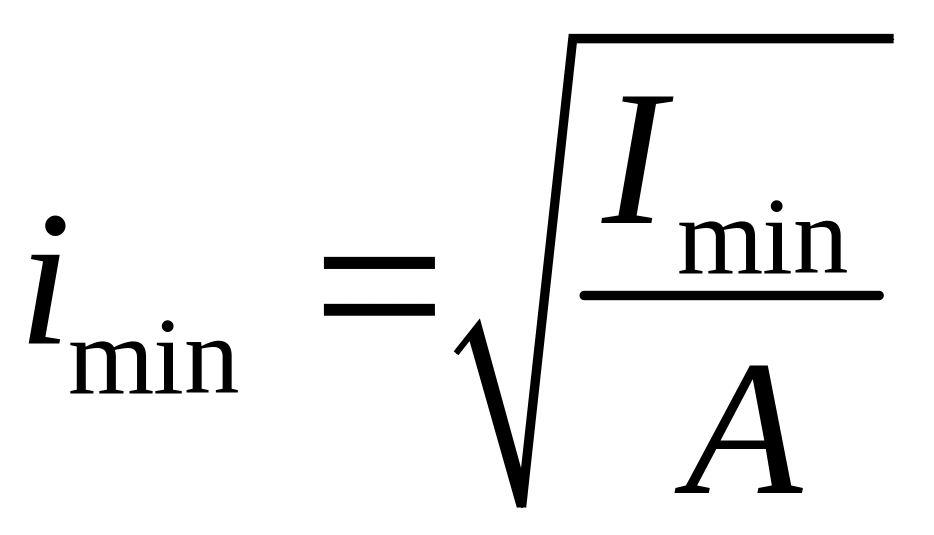- минимальный главный центральный радиус инерции поперечного сечения стойки; А – площадь поперечного сечения.

Если закрепление стержня в плоскостях наибольшей и наименьшей жесткости различно, то расчет следует вести по наибольшей гибкости, которая может соответствовать как максимальному, так и минимальному моменту инерции поперечного сечения стержня.

Формула Эйлера применима лишь в пределах справедливости закона Гука, т.е. при условии:

,

а значит , где 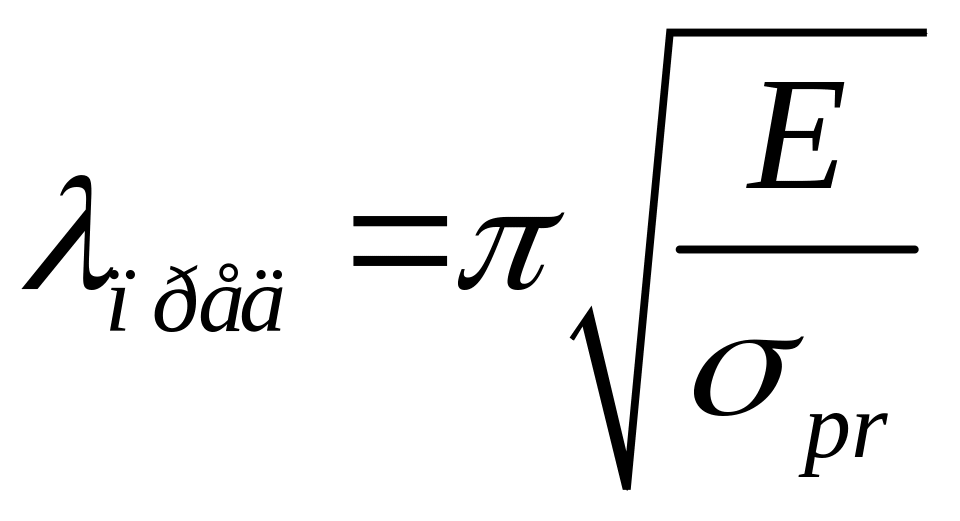- предельная гибкость для материала стержня, зависящая только от физико-механических свойств материала.

При гибкостях, меньших предельных, т.е. для стоек средней длины, критические напряжения определяются по формуле Ф.C. Ясинского:

,

a, b – коэффициенты, имеющие размерность напряжений, выбираются для различных материалов из таблиц.

Последовательность расчета стоек на устойчивость:

1. Определяется гибкость стойки .

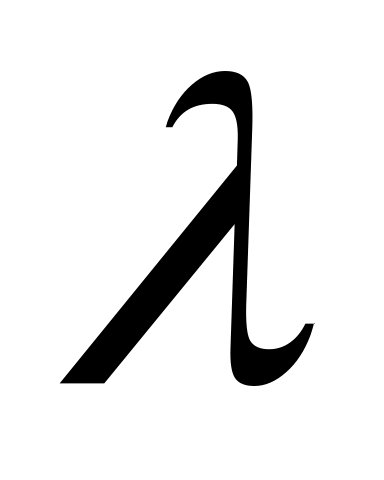2. Сопоставляется с предельной гибкостью .

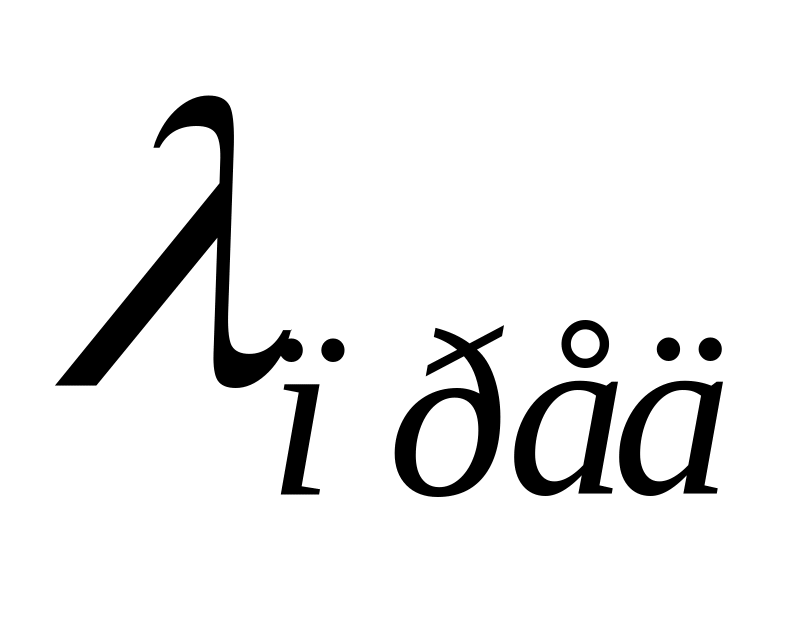В случае, если , то расчет производят по формуле Эйлера. Если , то критическое напряжение необходимо определять по формуле Ф.С. Ясинского.

Примечание. Часто вводится значение гибкости , при которой критическое напряжение равно предельному (опасному) напряжению при чистом сжатии. Поэтому при малой гибкости ( ) стержни рассчитывают не на устойчивость, а на прочность. Значения для различных материалов приводятся в таблице.

Практический интерес представляет способ расчета стоек на устойчивость по коэффициенту снижения допускаемого напряжения. В этом случае условие устойчивости имеет вид:

,

где F – сила, сжимающая стержень; А – площадь брутто (без учета местных ослаблений) поперечного сечения стержня; - допускаемое напряжение на сжатие; - коэффициент снижения допускаемого напряжения (коэффициент продольного изгиба), величина которого зависит от материала и гибкости, изменяется от 0 до 1 и выбирается из таблиц.

При решении задачи о подборе сечения в приведенном выше условии устойчивости одновременно присутствуют две неизвестные величины: и А. Задача решается путем последовательных приближений. Более подробно суть метода показана в примере расчета.