2.2. Пример расчёта статически неопределимой рамы

Для заданной (рис. 3 а) статически неопределимой рамы раскрыть статическую неопределимость и построить эпюры внутренних силовых факторов. Жёсткость всех стержней на изгиб одинакова и равна ЕI.

Исходные данные: q=10 кН/м, l =1 м.

Решение:

1. Определяем степень статической неопределимости: C=n-3,

где C- степень статической неопределимости; n = 5 – число опорных стержней;

C=5-3=2.

2. Выбираем основную систему. За лишние неизвестные принимаем связи неподвижной шарнирной опоры В.

3. Нагружаем основную систему заданной внешней нагрузкой и неизвестными реакциями Х1 и Х2 , возникающими в лишних связях. Получаем эквивалентную систему (рис. 3 б).

4. Составляем канонические уравнения метода сил:

11 Х1+ 12 Х2+ 1F =0,

21 Х1+ 22 Х2+ 2F =0.

5. Строим единичные (рис. 1.2 в, г) и грузовую (рис. 3 д) эпюры, с помощью которых вычисляем коэффициенты канонических уравнений.

Единичные перемещения ₁₁, ₂₂, ₁₂, ₂₁ находим перемножая в соответствующем порядке эпюры и :

;

;

.

Грузовые перемещения 1F и 2F получаем перемножением эпюры М_F поочередно на эпюры и .

1F = ;

2F = - .

6. Произведём проверку правильности нахождения коэффициентов. Для этого строим суммарную эпюру (рис. 3 е), нагружая основную систему одновременно силами и . Перемножаем по методу Верещагина и :

.

Находим алгебраическую сумму единичных перемещений:

.

Совпадение результатов показывает, что найдены правильно. Для проверки грузовых перемещений 1F и 2F перемножаем по способу Верещагина и :

.

Находим алгебраическую сумму грузовых перемещений 1F и 2F :

.

Совпадение результатов показывает, что найдены верно.

7. Подставляем коэффициенты и в канонические уравнения, и после сокращения на получаем:

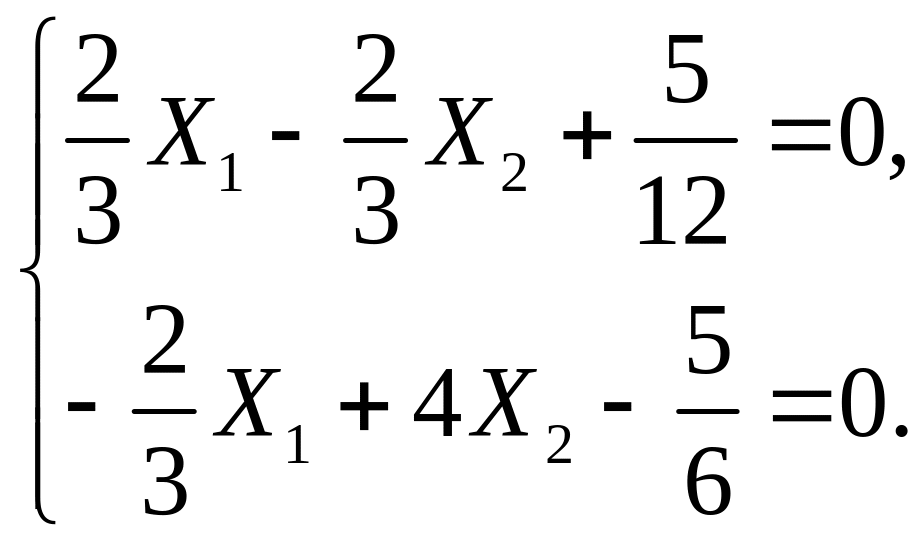
Решая полученную систему, находим:

и .

Проверяем правильность решения системы уравнений, подставляя в неё найденные значения Х1 и Х2:

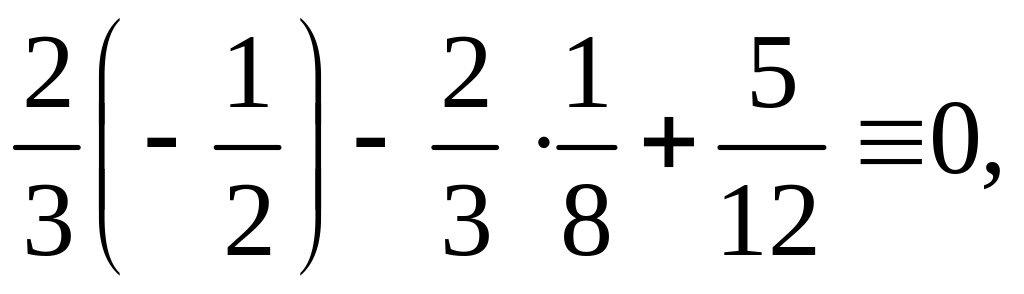
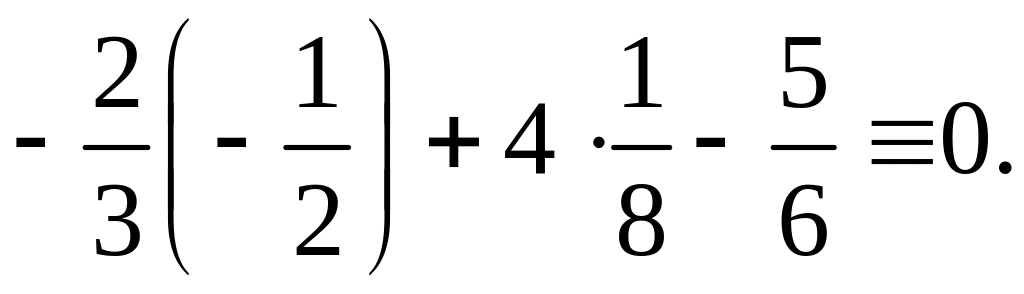
Канонические уравнения решены верно. Окончательно: , .

8. Составляя уравнения равновесия, определяем опорные реакции (рис. 3 ж), под действием заданной нагрузки и найденных значений Х1 и Х2 :

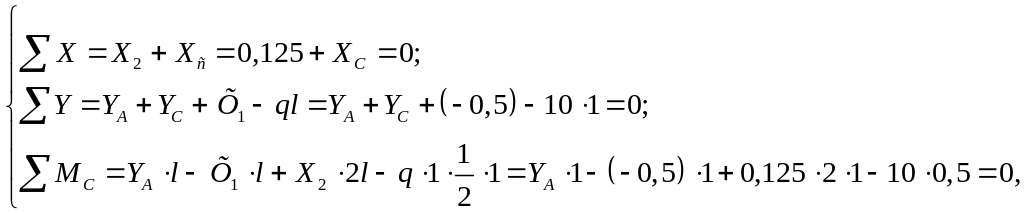
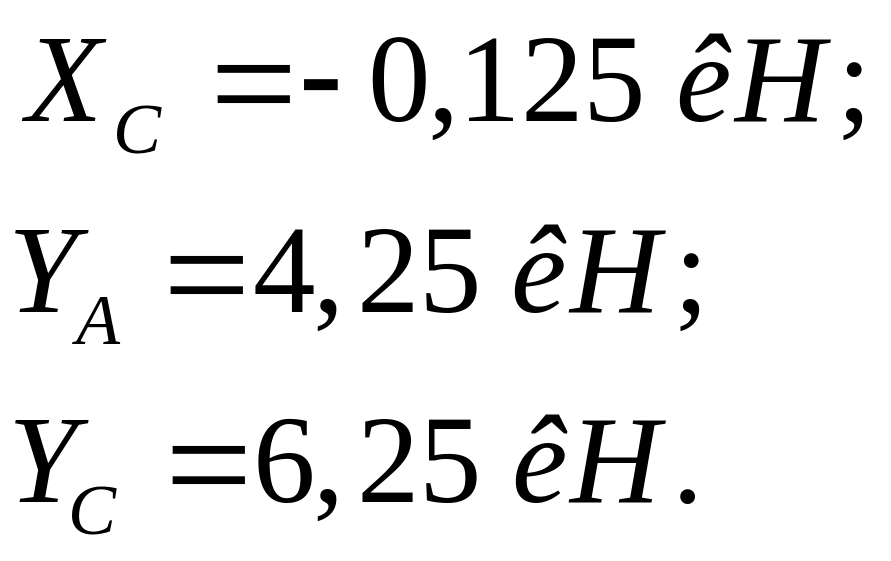
Проверка: .

Реакции найдены верно.

9. Окончательные эпюры M, Q, N легко построить обычным способо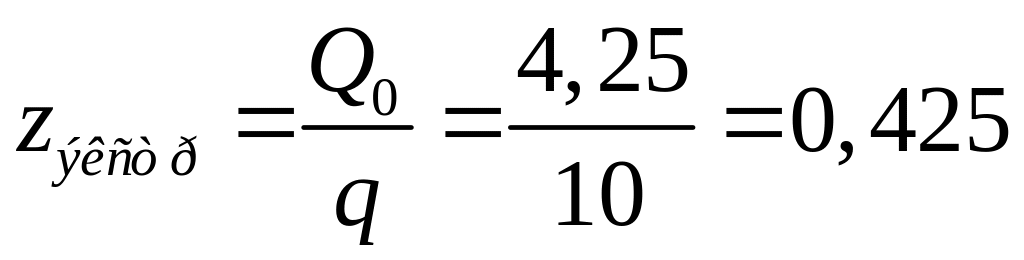м.

м;

.

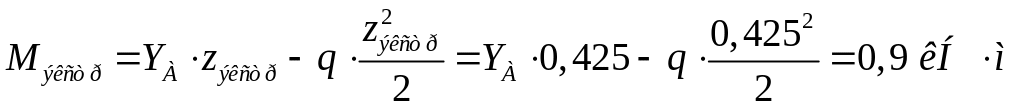10. Производим итоговые проверки полученных эпюр M, Q, N.

а) Статическая проверка (рис. 3 л):

Вырезаем узел Д. Заменяем действие отброшенных элементов усилиями, взятыми из построенных эпюр. Уравнения равновесия имеют следующий вид (рис. 3 к):

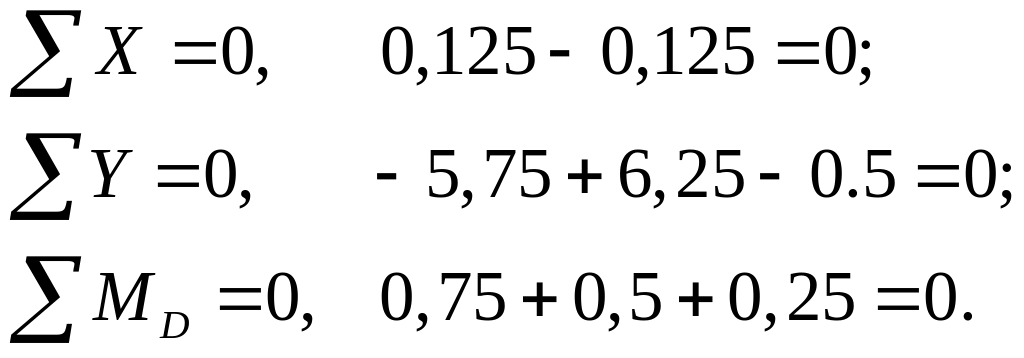
Проверяем равновесие всей рамы под действием внешней нагрузки и найденных реакций. Составим уравнение моментов сил относительно произвольно выбранной точки Е (рис. 3 ж):

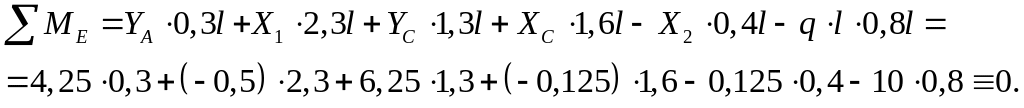
Все уравнения равновесия удовлетворяются.

б) Деформационная проверка.

Перемещения ₁ и ₂ рамы в направлении лишних неизвестных Х₁ и X₂ равны нулю. Перемножаем поочерёдно одну из единичных эпюр и эпюру М:

Для облегчения вычисления по методу Верещагина эпюру М на участке АD (рис. 3 м) рассматриваем состоящей из параболы (ниже оси) и треугольника (выше оси).

.

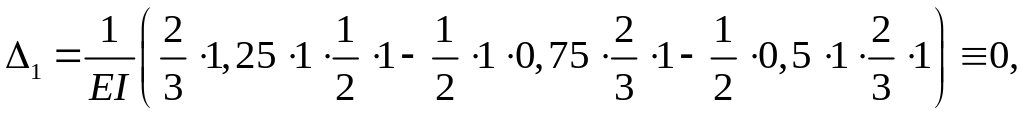
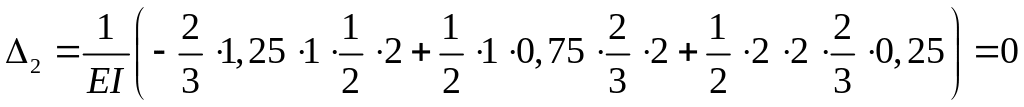Окончательная эпюра построена верно.