Лабораторна робота №4

Тема:Моделювання в реальному часі. Моделювання розповсюдження амплітудно-модульованого сигналу (хвилі) через середовище (канал зв’язку) з частотною дисперсією

Змоделювати “биття” синусоїдальної хвилі (рис. 2).

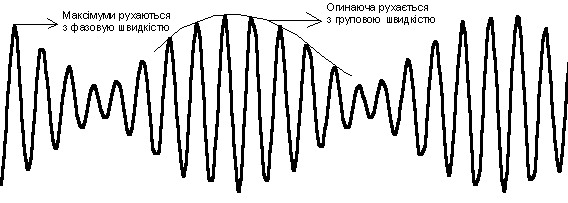
Рис.2

Хід роботи:

1. Розробити алгоритм (комп'ютерну програму).

Побудувати графік залежності у(t, х) від х для фіксованого значення часу т. Використовується розрахункова формула:

де А₁ = 100% — амплітуда першої синусоїдальної складової (прийнята за 1.0);

=100% — часова частота першої синусоїдальної складової (прийнята за 1.0);

=100% — просторова частота 1-ї синусоїдальної складової (прийнята за 1.0);

А₂ = 70% — амплітуда другої синусоїдальної складової (А₂ < А₁),

= 95% — часова частота другої синусоїдальної складової;

= 90% — просторова частота другої синусоїдальної складової;

— положення в просторі (для нашого чисельного прикладу х змінювався від 0 до 200 з кроком 1). Формула для кожного вводиться окремо.

2. Для того, щоб графік хвилі на екрані рухався, треба щоб змінна t змінювалася в реальному часі Для цього t вираховуємо за рекурсивною формулою: де — крок зміни часу, достатньо малий у порівнянні з періодом коливань. Для нашого прикладу було прийняте значення = 1 (період коливань ≈6). У випадку рекурсивних обчислень знак "=" означає операцію присвоювання, а не просто рівність.

При натисканні на клавішу F9 хвиля почне рухатися.

Зробити висновки:

1. Створена комп'ютерна модель дуже наглядно і просто ілюструє дуже важливі, але складні поняття частотної дисперсії в каналі зв'язку, групової і фазової швидкості розповсюдження сигналу завдяки моделюванню в реальному часі.

2. Моделювання в реальному часі вимагає рекурсивних обчислень, що синхронізуються зовнішніми або внутрішніми періодичними сигналами.

Звіт по роботі повинен складатися з:

1. Титульної сторінки.

2. Відображення ходу роботи та графіків .

3. Висновки.

Лабораторна робота №5

Тема: Дослідження стаціонарних режимів нелінійних систем та їх біфуркацій (катастроф).

В двох паралельних дротах протікає однаковий електричний струм в одному напрямі. Відомо, що дроти притягуються за рахунок електромагнітної взаємодії пропорційно квадрату струму і зворотньо пропорційно відстані між дротами. Притягання призводить до зближення дротів, але вважаємо, що при цьому вони залишаються паралельними. Притяганню протистоїть сила пружної деформації; яка збільшується пропорційно зміщенню дротів відносно початкового положення, за умови, що початкове положення ― відсутність струму.

Необхідно дослідити залежність зближення дротів від величини струму і виявити, коли настає біфуркація (катастрофа), тобто коли сила пружності вже не в змозі утримувати дроти і вони миттєво злипаються.

Хід роботи:

1. Побудувати сімейство графіків залежності F₁ і F₂ від х для різних значень параметра І за формулою:

:

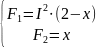
де х — зміщення дротів;

I - струм;

F₁ - сила електромагнітного притягання;

F₂ - сила пружного відштовхування;

Це і будуть статичні характеристики,

2. Проаналізувавши статичні характеристики, можна побудувати так звану біфуркаційну діаграму, яка ілюструє залежність зміщення в стаціонарних режимах від параметра (струму).

Зробити висновки:

1. Розглянута важлива практична задача з галузі електротехніки.

2. Задача сформульована у вигляді системи нелінійних рівнянь в безрозмірній формі,які мають декілька рішень (стаціонарних режимів). Стаціонарні режими знаходились за допомогою графіків, побудованих на екрані комп'ютера.

3.Результат дослідження представлено у вигляді статичних характеристик і біфуркаційної діаграми в безрозмірних координатах, що дає універсальну, наглядну і вичерпну картину усього явища. Подібний підхід досить часто зустрічається в моделюванні.

Звіт по роботі повинен складатися з:

1.Титульної сторінки.

2.Відображення ходу роботи та графіків .

3.Висновки.