Расчёт прогиба и механических напряжений в кремниевой мембране квадратной формы

Прогиб квадратной пластины, защемлённой по краям, определяется как сумма прогибов опёртой пластины, соответствующих трём видам воздействия:

,

где - прогиб опёртой равномерно нагруженной пластины,

- прогиб опёртой пластины, под действием компенсирующих моментов, распределённых по краям

- прогиб опёртой пластины, под действием компенсирующих моментов, распределённых по краям a/2.

Величина и распределение компенсирующих моментов подбирается так, чтобы результирующий поворот плоскости пластинки в местах заделки был равен нулю.

где

Прогиб пластинки действующими моментами:

1. распределёнными по краям и задаваемыми коэффициентами ,

2. распределёнными по краям и задаваемыми коэффициентами 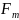, определится выражениями

Коэффициенты и определяются из условия компенсации углов поворота по краям пластинки в результате совместного действия всех трех видов нагружения.

Будем считать, что Коэффициенты и содержат один и тот же множитель, равный

Если вынести за знак суммы этот множитель, то прогибы пластинки под действием приложенных моментов примут вид

Множител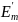и и имеют теперь только численные значения, для ифференцированием выражения (5) получаем

Сопоставляя выражения (4) и (5) можно видеть, что они симметричны относительно переменных и напряжения можно получить заменой переменных в выражениях (6) и (7):

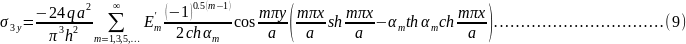
Напряжения в пластинке, закреплённой по краям, определяется суперпозицией напряжений, возникающих в трёх рассмотренных выше случаях видов её нагружения:

(10)

Построим график зависимости напряжений и от переменных и в виде поверхности над координатами соответствующих точек пластины.

В силу симметричности решаемой задачи, распределение напряжений и по площади пластины будет тоже симметричным. Поэтому приведём только распределение напряжений , рассчитанное по формуле (10). За единицу напряжения условно принят нормирующий множитель

.

Для численного определения напряжений необходимо подставить в полученные выражения параметры материала пластинки: для кремния принимаем модуль Юнга в направлении (111) коэффициент Пуассона плотность ρ = 2,33· кг/м³ , а также величину действующего давления.

Напряжения , действующие посередине пла­стины (x = 0,5, y = 0), приведенные на рис. 38, существенно превышают напряжения в её центре.

Рис. 38. Напряжения в квадратной мембране.

ПРИЛОЖЕНИЕ 3

Конструирование интегральных тензорезисторов

Исходными данными для расчёта геометрических размеров интегральных полупроводниковых резисторов являются: заданное в принципиальной электрической схеме номинальное значение сопротивление R и допуск на него ΔR; поверхностное сопротивление легированного слоя ρ_S, на основе которого формируется резистор; среднее значение мощности P и максимально допустимая удельная мощность рассеянья P₀; основные конструктивные и технологические ограничения. Поясним сначала понятие поверхностное сопротивление легированного слоя ρ_S.

Поверхностная электропроводность диэлектриков. Поверхностная электропроводность диффузионного резистора характеризуется значе­нием удельного поверхностного сопротивления ρ_S.

У проводниковых материалов поверхностные токи исчезающе малы по сравнению с объёмными токами; поэтому у этих материалов поверхностное сопротивление не учи­тывается.

Формальное определение удельного поверхностного сопротивления вытекает из следующих соображений. По­верхностное сопротивление участка поверхности твердо­го диэлектрика между параллельными друг другу кром­ками электродов длиной b, отстоящими друг от друга на расстоянии a, прямо пропорционально b и обратно пропорционально а. Если мыс­ленно разделим рассматриваемый участок поверхности на полоски линиями, параллельными кромкам электро­дов и проведёнными на расстоянии друг от друга, рав­ном единице, то увидим, что сопротивления этих полосок включаются последовательно. Если же разделим тот же участок поверхности линиями с расстоянием между ни­ми, также равным единице, но перпендикулярными кромкам электродов, то получим полоски, сопротивления которых включены параллельно друг другу. Следова­тельно, можем написать:

R_S = ρ_S (a/b),

где коэффициент пропорциональности ρ_S и есть удельное поверхностное сопротивление, ρ_S = R_S (b/a).

Очевидно, что размерность ρ_S совпадает с размерно­стью сопротивления. Выражая величину R_S в Омах (отношение b/a – безраз­мерное), получаем размерность величины ρ_S – Ом. Можно сказать, что ρ_S есть сопротивление квадрата (любого размера) на поверхности диэлектрика, если ток идёт от одной стороны квадрата к проти­воположной: при a = b формула дает R_S = ρ_S .

Иногда единицу ρ_S представ­ляют как «Ом на квадрат» (Ом/квадрат или Ом/м²). Такая запись обычна для проводнико­вых или полупроводниковых пле­нок, наносимых на диэлектриче­скую подложку (в частности, в микроэлектронике).

Используемая иногда едини­ца ρ_S – Ом/м² неправильна, так как удельное поверхностное со­противление отнюдь не относит­ся к единице поверхности мате­риала.

Если изменить конфигурацию участка на поверхности мате­риала между краями электродов, между которыми определяется поверхностное сопротивление, на другую, геометрически подобную прежней, то значение поверх­ностного сопротивления меж­ду этими электродами на данном материале (при сохранении значения ρ_S) не изменится. Для случая объёмного сопротивления этот «закон подобия» не имеет силы.

Полная относительная погрешность сопротивления диффузионного резистора определяется суммой погрешностей:

где K_φ – коэффициент формы резистора;

– относительная погрешность коэффициента формы резистора;

– относительная погрешность воспроизведения удельного поверхностного сопротивления легированного слоя, для типовых технологических процессов

= 0,05 0,1;

температурный коэффициент сопротивления резистора, = (0,5 3)·10^-3 1/°C,

– температурная погрешность сопротивления.

Принимаем, что интегральный полупроводниковый резистор в сечении, перпендикулярном направлению протекания тока, имеет прямоугольную форму.

Расчёт геометрических размеров интегрального полупроводникового резистора начинают с определения его ширины. За расчётную ширину b_расч резистора принимают значение, которое не меньше наибольшего из трёх величин: b_техн , b_точн , b_P, т. е.

где b_техн – минимальная ширина резистора, определяемая разрешающей способностью технологических процессов;

b_точн – минимальная ширина резистора, при которой обеспечивается заданная погрешность геометрических размеров;

b_P – минимальная ширина резистора, определяемая из максимально допустимой мощности рассеянья.

Величину b_техн находят из перечня технологических ограничений выбранной технологии (например, для планарно-эпитаксиальной технологии b_техн = 5мкм).

Ширину b_точн определяют из выражения

где и – абсолютные погрешности ширины и длины резистивной полоски, обусловленные технологическими процессами.

Для типовых технологических процессов ( = = 0,05 0,1 мкм).

Ширину b_P определяют из выражения

где P₀ – максимально допустимая удельная мощность рассеяния, выбираемая в зависимости от типа корпуса микросхемы и условий ее эксплуатации в пределах 0,5 – 4,5 Вт/мм².

Про­межуточное значение ширины резистора:

где Δ_трав – погрешность, вносимая за счёт растравливания окон в маскирующем окисле перед диффузией. Для типовых технологиче­ских процессов величина Δ_трав = 0,2 0,5 мкм. Погрешность Δу, вносимая за счёт ухода диффузионного слоя под маскирующий окисел в бо­ковую сторону, ориентировочно составляют 60% глубины ба­зового слоя и 80% глубины эмиттерного слоя.

Далее находят топологическую ширину резистора b_топ (ширину на чертеже топологии) и реальную ширину резистора на кристалле после изготовления ИМС.

Если b_пром ≥ b_техн, то за b_топ принимают равное или ближайшее к b_пром большее значение, кратное шагу координатной сетки, при­нятому для чертежа топологии.

Реальная ширина резистора на кристалле

Если в b_пром b_техи, то за b_топ принимают равное или ближай­шее к b_техн большее значение, кратное шагу координатной сетки. Реальную ширину резистора на кристалле определяют так же, как и в первом случае.

Расчетную длину резистора определяют по формуле

где N_изг – количество изгибов резистора на угол π/2; k₁, k₂ – по­правочные коэффициенты, учитывающие сопротивление контактных областей резистора (рис. 39), зависящее от конфигурации контактной области резистора, соотношения разме­ров контактного окна L₁, контактной области L₂ и реальной ширины резистора b с каждой его стороны; n₁ и n₂— число контактных пло­щадок (обычно п =2).

Рис. 39. Значения коэффициентов k₁ и k₂ для расчета диффузионных резисторов при различных конструкциях контактных областей: а, е – для низкоомных резисторов; б, в – для высокоомных резисторов

Следует учитывать, что реальная длина резистора l на кристал­ле будет меньше топологической длины l_топ на чертеже топологии за счёт увеличения геометрических размеров контактных областей резистора с обоих концов в результате боковой диффузии, поэтому, сначала оценивают промежуточное значение длины резистора.

За топологическую длину резистора l_топ принимают ближайшее к l_пром значение длины, кратное шагу координатной сетки, приня­тому для чертежа топологии.

Отклонение размеров резистивной области за счёт погрешно­стей Δ_трав и Δy следует обязательно учитывать при определении величин L₁ и L₂ и выборе коэффициентов k₁ и k₂.

При окончательном определении топологических значений b_топ и l_топ рассчитывают сопротивление спроектированного резистора и погрешность, используя реальные значения ширины и длины ре­зистора на кристалле. При необходимости увеличивают ширину или длину резистора до значения, дающего приемлемую погреш­ность. Конфигурации диффузионных резисторов приведены на рис. 40.

Рис. 40 Конфигурации диффузионных резисторов

Сопротивление резисторов определяют по формулам:

для резисторов рис. 40, а, б, г, д

для резистора рис. 40, в

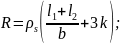
для резистора рис. 40, е

где – суммарная длина прямолинейных участков,

– поверхностное сопротивление базового слоя.