
- •1. Понятие физической величины. Система физических величин
- •2. Международная система единиц си
- •3. Производные единицы си
- •4. Кратные и дольные единицы си
- •5. Внесистемные единицы физических величин
- •6. Единицы физических величин, подлежащих применению в строительстве
- •7. Измерение физических величин. Понятия и определения
- •8. Средства измерений, испытаний и контроля
- •9. Средства измерений, используемые в строительстве
- •10. Методы измерений. Определения и виды
- •11. Классификации методов измерений
- •12. Ошибки измерений и их виды
- •13. Погрешность измерений – мера точности результата
- •14. Гистограмма и распределение Гаусса
- •15. Анализ кривой Гаусса. Точные и эмпирические формулы для средних величин
- •16. Доверительный интервал и доверительная вероятность
- •17. Распределение Стьюдента
- •18. Определение необходимого числа измерений
- •19. Обнаружение грубых ошибок
- •20. Основные правила проведения измерений
- •21. Измерение геометрических параметров и углов
- •22. Линейки измерительные, штангенциркули и микрометры
- •23. Измерение времени и массы
- •24. Приборы для измерения температуры
- •25. Электроизмерительные приборы (общие сведения)
- •26. Магнитоэлектрические (I) и электромагнитные (II) измерительные приборы
- •27. Электродинамические измерительные приборы (I), ваттметры (II)
- •28. Электростатические (I) и электронные (II) вольтметры
- •29. Испытания продукции (понятия и определения)
- •30. Основные виды испытаний продукции
- •31. Контроль качества продукции (задачи и виды контроля)
- •32. Структура и функции отк
- •33. Определение истинной и средней плотности строительных материалов
- •34. Определеннее насыпной плотноcти, пористости и водопоглощения строительных материалов
- •35. Ареометрический метод определения плотности жидкостей
- •36. Гидрофизические свойства строительных материалов (гигроскопичность, капиллярное всасывание, водопоглощение)
- •37. Методы определения водостойкости, газо- и паропроницаемости
- •38. Морозостойкость строительных материалов и ее определение
- •39. Определение прочности строительных материалов
- •40. Испытания строительных металлов на растяжение
- •41. Определение характеристик песка (плотность, пустотность, влажность, примеси, зерновой состав)
- •42. Определение характеристик щебня и гравия
- •43. Определение физических и механических свойств древесины
- •44. Теплофизические свойства и их определение
- •45. Проблема «состав-строение-свойство». Элементный состав и методы его определения
- •46. Фазовый состав и методы его определения
- •47. Химический состав и методы его определения
- •48. Рентгеновское излучение. Устройство рентгеновской трубки
- •49. Спектр излучения рентгеновской трубки
- •50. Характеристическое рентгеновское излучение. Закон Мозли
- •51. Закон Вульфа-Брэгга и его использование в методах анализа
- •52. Метод рентгенофлюоресцентного анализа
- •53. Метод рентгенофазового анализа
- •54. Термические методы анализа
17. Распределение Стьюдента
При ограниченном числе измерений (n 20) закон распределения ошибок в реальном эксперименте описывается функцией Стьюдента, которая имеет вид

где
![]() – гамма-функция, значения которой при
1 m
2 табулированы, а
для m < 1 и m
> 1 используют рекуррентное соотношение
Г(m+1) = mГ(m).
– гамма-функция, значения которой при
1 m
2 табулированы, а
для m < 1 и m
> 1 используют рекуррентное соотношение
Г(m+1) = mГ(m).
Найдем вид (x, n) для предельно низкого значения n = 2 и δ = 1, воспользовавшись табличными значениями Г(1) = 1 и Г(1,5) = 0,886, а также рекуррентным соотношением Г(1,5) = 0,5Г(0,5). Это выражение, как нетрудно показать, будет иметь следующий вид
![]()
Данные распределение называется лоренцовским, которое в сравнении с распределением Гаусса характеризуется более длинными хвостами. Легко показать, что мы не ошиблись при нахождении (х, 2); проинтегрировав это выражение от -∞ до ∞. Получим, что интеграл этот равен единице, как и должно быть для нормированного на 1 распределения ошибок в эксперименте (интеграл этот находится с использованием таблиц).
Сравним оба распределения
– гауссовское и лоренцовское – на
рисунке, приведенном ниже. Учтем при
этом, что (0, 2) = 1/π,
а (0, ∞) = 1/![]() ,
,
с учетом чего (0, 2)/(х, ∞) = /π = 0,8.
Видно, что высота распределения Стьюдента при n = 2 понижается на 20% в сравнении с высотой распределения Гаусса, а крылья линии становятся более протяженными.
При малых n
как доверительный интервал, так и
доверительная вероятность зависят от
числа измерений n.
Существуют справочные таблицы, которые
связывают между собой доверительный
интервал и доверительную вероятность
при разных n. При этом
доверительный интервал измеряют обычно
в безразмерных единицах, которые
определяют по формуле ts
= ε![]() .
Эти величины называют коэффициентами
Стьюдента.
.
Эти величины называют коэффициентами
Стьюдента.
При работе с распределением Стьюдента вместо таблиц 1, 2 для распределения Гаусса существуют таблицы 3, 4, которые в упрощенном виде приведены ниже. Из таблиц 3, 4 видно, что понижение числа измерений ведет к увеличению доверительного интервала и понижению доверительной вероятности, т.е. к снижению точности измерений.
Таблица 3. Доверительные вероятности Р(ts) при разных n |
|
Таблица 4. Значения ts как функция Р при разных n |
||||||
n |
1 |
2 |
3 |
P n |
0,50 |
0,95 |
0,99 |
|
2 10 20 ∞ |
0,500 0.650 0,670 0,683 |
0,700 0,930 0,940 0,995 |
0,800 0,985 0,993 0,997 |
2 10 20 ∞ |
1 0,70 0,69 0,675 |
13 2,26 2,09 1,960 |
64 3,25 2,86 2,576 |
|
18. Определение необходимого числа измерений
Доверительный интервал ε, характеризующий величину случайной погрешности, при заданном числе измерений n можно записать в виде
![]()
где ts – коэффициент Стьюдента, а S – среднее квадратичное отклонение результатов для серии измерений.
Как видно из формулы, доверительный интервал можно уменьшать как за счет увеличения точности измерений (уменьшения S), так и за счет увеличения числа измерений (увеличение n). Возникает чисто практический вопрос: можно ли определить (оценить) оптимальное число измерений, чтобы обеспечить необходимую погрешность при заданной доверительной вероятности? Да, можно, и для такой оценки существует приведенная ниже таблица 5 (упрощенная форма), из которой, задав величину интервала t в безразмерных единицах ε/S и вероятность Р, находят n.
Таблица 5. Значения n как функция t и P
-
P
t
0,5
0,9
0,95
0,99
1
0,5
0,4
0,3
2
3
4
6
5
13
19
32
7
18
27
46
11
31
46
78
Ясно, что уменьшать случайную погрешность ε имеет смысл до тех пор, пока она не сравнится с систематической погрешностью δ0, определяемой классом точности прибора. На практике для определения оптимального числа измерений n используют обычно следующие равенства: ε = δ0 и ε = 0,5δ0, учитывая которые, задают ε, после чего из табл. 5 находят n.

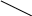 ts
ts